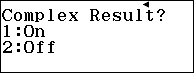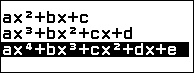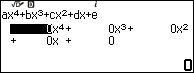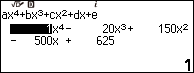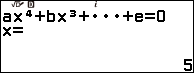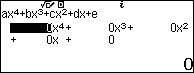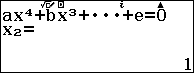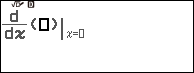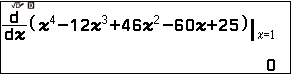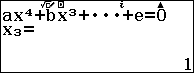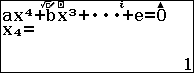Cách kiểm tra nghiệm là bội mấy bằng Casio 880 & 580

Chào bạn, hôm nay mình sẽ hướng dẫn các bạn cách kiểm tra nhanh nghiệm của đa thức bậc bốn là nghiệm bội mấy bằng máy tính CASIO nha.

Việc kiểm tra này rất hữu ích trong quá trình học tập, kiểm tra và thi cử, tiêu biểu là:

• Xét dấu đa thức bậc bốn.
• Chia đa thức bậc bất kì cho đa thức bậc bốn.
• Một số bài toán trong các môn Đại số tuyến tính, Phương trình vi phân, Hình học Ơ Clít
• …

#1. Các trường hợp nghiệm của đa thức bậc bốn

Trước hết, các bạn nên biết là khi nói đến nghiệm bội chẵn, bội lẻ thì có nghĩa là đang nói đến nghiệm thực, còn nghiệm phức không có các khái niệm này.

• Nghiệm đơn là trường hợp đặc biệt của nghiệm bội lẻ (nghiệm bội một),
• Nghiệm kép là trường hợp đặc biệt của nghiệm bội chẵn (nghiệm bội hai).

Một đa thức bậc bốn khi nói đến nghiệm thực chỉ có thể rơi vào một trong năm trường hợp:

• Trường hợp 1: 1 nghiệm bội bốn.
• Trường hợp 2: 1 nghiệm bội ba và 1 nghiệm đơn.
• Trường hợp 3: 1 nghiệm bội kép và 1 nghiệm kép,
• Trường hợp 4: 1 nghiệm kép, 1 nghiệm đơn và 1 nghiệm đơn.
• Trường hợp 5: 1 nghiệm đơn, 1 nghiệm đơn, 1 nghiệm đơn và 1 nghiệm đơn.

#2. Cài đặt hiển thị nghiệm phức trên máy Casio

Mặc định thì nghiệm phức sẽ tự động hiển thị khi giải phương trình, trong trường hợp nghiệm phức không hiển thị thì bạn cần thực hiện tuần tự theo các bước.

#2.1. Cài đặt trên máy fx 880 BTG

Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK

Bước 2. Chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK

Bước 3. Nhấn phím TOOLS => chọn Complex Roots => nhấn phím OK => chọn On => nhấn phím OK

Bước 4. Nhấn phím AC

#2.2. Cài đặt trên fx 580 VN X

Bước 1. Nhấn phím SHIFT => nhấn phím MENU

Bước 2. Nhấn phím

Bước 3. Nhấn phím 4

Bước 4. Nhấn phím 1

#3. Tính năng Derivative / $\frac{d}{dx}$

Tính năng Derivative / $\frac{d}{dx}$ của máy tính CASIO cho phép chúng ta tính đạo hàm tại một điểm bất kỳ.

• $x_0$ là nghiệm của đa thức và không là nghiệm của đạo hàm cấp một của đa thức tại $x_0$ thì $x_0$ là nghiệm đơn.
• $x_0$ là nghiệm của đa thức và là nghiệm của đạo hàm cấp một của đa thức tại $x_0$ và không là nghiệm của đạo hàm cấp hai của đa thức tại $x_0$ thì $x_0$ là nghiệm kép.

Bằng cách sử dụng linh hoạt #1 và #3 chúng ta có thể xác định nghiệm của một đa thức bậc bốn bất kỳ là nghiệm bội mấy một cách chính xác và nhanh chóng.

#4. Thuật toán kiểm tra nghiệm bội

Sử dụng tính năng Equation (Polynomial) giải phương trình bậc bốn tương ứng rồi suy luận theo các gợi ý:

Nếu đa thức có 1 nghiệm thì là nghiệm bội bốn.

Nếu đa thức có 4 nghiệm thì là nghiệm đơn.

Nếu đa thức có 3 nghiệm thì sẽ có một nghiệm kép và hai nghiệm đơn.

Lúc này chúng ta sử dụng Derivative để kiểm tra xem nghiệm nào là nghiệm kép.

Nếu đa thức có 2 nghiệm thì sẽ rơi vào Trường hợp 2: 1 nghiệm bội ba và 1 nghiệm đơn hoặc Trường hợp 3: 1 nghiệm bội kép và 1 nghiệm kép.

Lúc này, bạn sử dụng tính năng Derivative kiểm tra xem nghiệm nào là nghiệm đơn.

Giả sử hai nghiệm tìm được là $x_1$ hoặc $x_2$.

• Nếu $x_1$ là nghiệm đơn thì $x_2$ là nghiệm bội ba.
• Nếu $x_2$ là nghiệm đơn thì $x_1$ là nghiệm bội.
• Nếu $x_1$ và $x_2$ không là nghiệm đơn thì $x_1$ và $x_2$ là nghiệm kép.

#5. Thực hành kiểm tra nghiệm bội mấy bằng máy Casio

Ví dụ 1. Đa thức bậc bốn $x^4 – 20 x^3 + 150 x^2 – 500 x + 625$ có nghiệm là gì? Chỉ rõ nghiệm tìm được là nghiệm bội mấy?

5.1. Thực hành trên fx 880 BTG

Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^4+bx^3+cx^2+dx+e$ => nhấn phím OK

Bước 2. Nhập 1 => nhấn phím EXE => nhập -20 => nhấn phím EXE => nhập 150 => nhấn phím EXE => nhập -500 => nhấn phím EXE => nhập 625 => nhấn phím EXE

Bước 3. Nhấn phím EXE

Vì đa thức bậc bốn đã cho chỉ có một nghiệm thực là 5 nên 5 là nghiệm bội bốn.

5.2. Thực hành trên fx 580 VN X

Bước 1. Nhấn phím MENU => nhấn phím 9 => nhấn phím 2 => nhấn phím 4

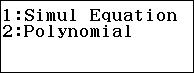
Bước 2. Nhập 1 => nhấn phím = => nhập -20 => nhấn phím = => nhập 150 => nhấn phím = => nhập -500 => nhấn phím = => nhập 625 => nhấn phím =

Bước 3. Nhấn phím =

Vì đa thức bậc bốn đã cho chỉ có một nghiệm thực là 5 nên 5 là nghiệm bội bốn.

Ví dụ 2. Đa thức bậc bốn $x^4 – 10 x^3 + 24 x^2 – 22 x + 7$ có nghiệm là gì? Chỉ rõ nghiệm tìm được là nghiệm bội mấy?

5.3. Thực hành trên fx 880 BTG

Thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta tìm được hai nghiệm thực là 7 và 1

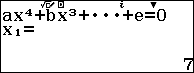
Vì đa thức bậc bốn đã có hai nghiệm thực nên sẽ rơi vào Trường hợp 2: 1 nghiệm bội ba và 1 nghiệm đơn hoặc Trường hợp 3: 1 nghiệm bội kép và 1 nghiệm kép.

Bước 4. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

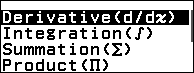
Bước 5. Nhập $x^4 – 10 x^3 + 24 x^2 – 22 x + 7$ => nhấn phím  nhập 7

 

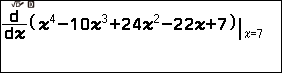
Bước 6. Nhấn phím EXE

Vì $\frac{d}{dx}(x^4-10x^3+24x^2-22x+7)|_{x=7}=216$ (khác 0) nên 7 là nghiệm đơn và 1 là nghiệm bội ba.

5.4. Thực hành trên fx 580 VN X

Thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta tìm được hai nghiệm thực là 7 và 1

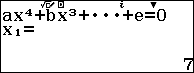
Vì đa thức bậc bốn đã cho có hai nghiệm thực nên sẽ rơi vào Trường hợp 2: 1 nghiệm bội ba và 1 nghiệm đơn hoặc Trường hợp 3: 1 nghiệm kép và 1 nghiệm kép.

Bước 4. Nhấn phím SHIFT => nhấn phím

Bước 5. Nhập $x^4 – 10 x^3 + 24 x^2 – 22 x + 7$ => nhấn phím  nhập 7

Bước 6. Nhấn phím =

Vì $\frac{d}{dx}(x^4-10x^3+24x^2-22x+7)|_{x=7}=216$ (khác 0) nên 7 là nghiệm đơn và 1 là nghiệm bội ba.

Ví dụ 3. Đa thức bậc bốn $x^4 – 12 x^3 + 46 x^2 – 60 x + 25$ có nghiệm là gì? Chỉ rõ nghiệm tìm được là nghiệm bội mấy?

Thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta tìm được hai nghiệm thực là 5 và 1

Vì đa thức bậc bốn đã cho có hai nghiệm thực nên sẽ rơi vào Trường hợp 2: 1 nghiệm bội ba và 1 nghiệm đơn hoặc Trường hợp 3: 1 nghiệm bội kép và 1 nghiệm kép.

Thực hiện Bước 4 đến Bước 6 của Ví dụ 2 chúng ta được $\frac{d}{dx}(x^4 – 12 x^3 + 46 x^2 – 60 x + 25)|_{x=5}=0$ và $\frac{d}{dx}(x^4 – 12 x^3 + 46 x^2 – 60 x + 25)|_{x=1}=0$

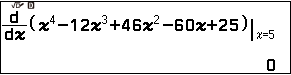
Vì đa thức bậc bốn đã cho có hai nghiệm thực và đạo hàm cấp một của đa thức bậc bốn đã cho tại hai nghiệm này đều bằng 0 nên 5 và 1 là hai nghiệm kép.

Chú ý.
Nếu chỉ có $\frac{d}{dx}(x^4 – 12 x^3 + 46 x^2 – 60 x + 25)|_{x=5}=0$ mà đã vội kết luận 5 là nghiệm kép thì với các đa thức bậc bốn khác có thể sai.

Ví dụ 4. Đa thức bậc bốn $x^4 – 14 x^3 + 68 x^2 – 130 x + 75$ có nghiệm là gì? Chỉ rõ nghiệm tìm được là nghiệm bội mấy?

Thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta tìm được hai nghiệm thực là 5, 3 và 1

Vì đa thức bậc bốn đã cho có ba nghiệm thực nên sẽ có một nghiệm kép và hai nghiệm đơn.

Thực hiện tương tự Bước 4 đến Bước 6 của Ví dụ 2 chúng ta được $\frac{d}{dx}(x^4 – 14 x^3 + 68 x^2 – 130 x + 75)|_{x=5}=0$

Vì đạo hàm cấp một của đa thức bậc bốn đã cho tại 5 bằng 0 nên 5 là nghiệm kép, 3 và 1 là nghiệm đơn.

Ví dụ 5. Đa thức bậc bốn $x^4 – 16 x^3 + 86 x^2 – 176 x + 105$ có nghiệm là gì? Chỉ rõ nghiệm tìm được là nghiệm bội mấy?

Thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta được bốn nghiệm là 7, 5, 3 và 1

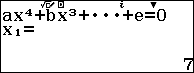
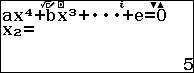
Vì đa thức bậc bốn đã cho có bốn nghiệm thực nên bốn nghiệm này đều là nghiệm đơn.

#6. Lời kết

Trường hợp đa thức bậc bốn vừa có nghiệm thực, vừa có nghiệm phức thì vẫn có thể dựa theo những chỉ dẫn trong bài viết này để kiểm tra nhưng cần thực hiện thêm một số thao tác phù hợp.

Bạn nên biết rằng một nghiệm của một phương trình bậc bốn làm cho đạo hàm bằng không có thể là nghiệm kép hoặc nghiệm bội ba hoặc bội bốn, khi kiểm tra phải hết sức cẩn thận.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn