Xin chào tất cả các bạn, hôm nay mình sẽ tiếp tục hướng dẫn cho các bạn cách viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
Xét về bản chất thì bài viết này là sự kết hợp giữa bài viết cách tìm cực trị của hàm số đa thức và bài viết cách viết phương trình đường thẳng nằm trên mặt phẳng mà mình đã chia sẻ trước đó.
Vậy nên, nội dung chính của bài viết này chính là phần nội dung kết hợp của hai bài viết trên. Tuy nhiên trong bài viết này mình sẽ giới thiệu thêm …
- Công thức viết nhanh phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc ba và hàm phân thức.
- Thủ thuật viết nhanh phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc ba bằng máy tính CASIO.
Okay, bắt đầu thôi nào…
Mục Lục Nội Dung
Trường hợp #1. Đường thẳng đi qua hai điểm cực trị của hàm số bậc ba
Ở đây mình chọn hướng dẫn riêng cho hàm số bậc ba $f(x)=ax^3+bx^2+cx+d$ với $a \neq 0$ là vì hàm số này rất thường gặp trong các đề kiểm tra, hoặc đề thi.
Ngoài viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc ba thì đề bài còn có thể yêu cầu bạn:
- Tính khoảng cách giữa hai điểm cực trị.
- Tìm trung điểm.
- Viết phương trình đường tròn đi qua hai điểm cực trị và nhận khoảng cách giữa hai điểm cực trị làm đường kính.
Cách 1. Sử dụng kiến thức Toán học
Về cơ bản thì các bước như sau:
Bước 1. Tìm hai điểm cực trị của hàm số bậc ba.
Xem thêm: Cách tìm cực trị của hàm số đa thức.
Bước 2. Viết phương trình đường thẳng đi qua hai điểm cực trị vừa tìm được.
Xem thêm: Cách viết phương trình đường thẳng nằm trên mặt phẳng.
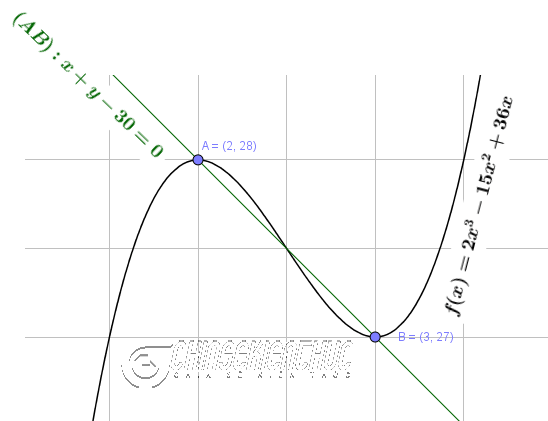
Ví dụ 1. Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số $f(x)=2x^3-15x^2+36x$
Lời giải:
Vì $f(x)=2x^3-15x^2+36x$ là hàm đa thức bậc ba, vậy nên tập xác định của nó là R.
$f’(x)=6(x^2-5x+6)$
$f’(x)=0 \Leftrightarrow 6(x^2-5x+6)=0 \Leftrightarrow 6(x-2)(x-3)=0$
Suy ra $x=2$ và $x=3$ là nghiệm của phương trình $f’(x)=0$
Suy ra hai điểm cực trị của đồ thị hàm số đã cho là A=(2; 28) và B=(3; 27)
Phương trình đường thẳng đi qua hai điểm A, B là $\frac{x-2}{3-2}=\frac{y-28}{27-28}$ hay $\frac{x-2}{1}=\frac{y-28}{-1}$ hay $x+y-30=0$
Vậy => phương trình đường thẳng cần tìm là $x+y-30=0$
Nhận xét:
Cách này tuy hơi dài một chút nhưng đây là cách giải chính thống, cách này có thể viết được phương trình đường thẳng đi qua hai điểm của mọi hàm số chứ không chỉ riêng hàm số bậc ba nha các bạn.
Cách 2. Sử dụng công thức đặc biệt
Nếu may mắn phương trình đường thẳng cần tìm đi qua hai điểm cực trị của hàm số bậc ba thì bạn có thể áp dụng công thức đặc biệt bên dưới để viết nhanh hơn.
+) Công thức đặc biệt
Nếu hàm số bậc ba $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị thì phương trình đường thẳng đi qua hai điểm cực trị sẽ là: $y=-\frac{2}{9a}(b^2-3ac)x+d-\frac{bc}{9a}$
Ví dụ 2. Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số $f(x)=2x^3-15x^2+36x$
Lời giải:
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Phương trình đường thẳng cần tìm có dạng $y=-\frac{2}{9a}(b^2-3ac)x+d-\frac{bc}{9a}$ hay $y=-\frac{2}{9.2}((-15)^2-3.2.36)x+0-\frac{(-15).36}{9.2}$ hay $y=-x+30$
Vậy phương trình đường thẳng cần tìm là $y=-x+30$
+) Sử dụng máy tính CASIO để giải
Bước 1. Lần lượt gán các giá trị 2, -15, 36, 0 vào các biến nhớ A, B, C, D <xem cách gán giá trị trong bài viết này nếu bạn chưa biết. Trong phần 2.2 của Cách #2>
Bước 2. Nhập đa biểu thức:
Chú ý: Phím
:được nhập bằng cách nhấn
Bước 3. Nhấn phím = => tiếp tục nhấn phím = phát nữa.
Cách 3. Sử dụng máy tính CASIO
Ví dụ 3. Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số $f(x)=2x^3-15x^2+36x$
Chú ý:
Trong các dòng máy tính CASIO được phép mang vào phòng thi chỉ có máy tính CASIO fx-580VN X là áp dụng được thủ thuật này.
Các bước thực hiện:
Bước 1. Chọn phương thức tính toán Equation / Func
Bước 2. Chọn Polynomial
Bước 3. Chọn bậc của đa thức (vì bậc của đa thức là ba nên chúng ta sẽ nhấn phím số 3)
Bước 4. Nhập các hệ số …
Bước 5. Nhấn phím = = > nhấn phím = => nhấn phím =
Bước 6. Nhấn phím = => nhấn phím
Bước 7. Nhấn phím = => nhấn phím
Bước 8. Nhấn phím = => nhấn phím
Bước 9. Nhấn phím = => nhấn phím
Bước 10. Nhấn phím OPNT => chọn Simul Equation
Bước 11. Chọn số phương trình của hệ (vì hệ phương trình ở đây là hệ hai phương trình bậc nhất hai ẩn nên chúng ta sẽ nhấn phím số 2).
Bước 12. Nhập các hệ số của hệ phương trình $\left\{\begin{array}{ll}Ax+y&=B\\Cx+y&=D\end{array}\right.$
Bước 13. Nhấn phím = => nhấn tiếp phím =
Vậy phương trình đường thẳng cần tìm là $y=-x+30$
Lời bình …
- Bước 1 đến Bước 5 là giải phương trình bậc ba tương ứng.
- Bước 6 đến Bước 9 là gán hoành độ và trung độ của hai điểm cực trị vào các biến nhớ (đối với hàm bậc ba này bạn có thể không gán vì hoành độ và trung độ của hai điểm cực trị có giá trị. nguyên, trường hợp có giá trị hữu tỉ hoặc có chứa căn thức thì nhất thiết phải gán).
- Bước 10 đến Bước 13 là viết phương trình đường thẳng đi qua hai điểm.
Trường hợp #2. Đường thẳng đi qua hai điểm cực trị của hàm số phân thức
Hàm số phân thức được nhắc đến ở đây chính xác là hàm số $f(x)=\frac{ax^2+bx+c}{b’x+c’}$
Nếu hàm số $f(x)=\frac{ax^2+bx+c}{b’x+c’}$ có hai điểm cực trị thì phương trình đường thẳng đi qua hai điểm cực trị này là $y=\frac{2ax+b}{b’}$
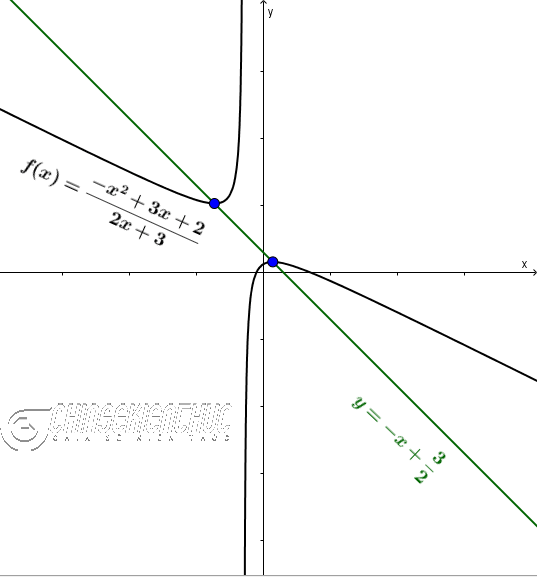
Ví dụ 4. Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số $f(x)=\frac{-x^2+3x+2}{2x+3}$
Lời giải:
Phương trình đường thẳng cần tìm có dạng $y=\frac{2ax+b}{b’}$ hay $y=\frac{2(-1)x+3}{2}$ hay $y=-x+\frac{3}{2}$
Trường hợp #3. Đường thẳng đi qua hai điểm cực trị của hàm số bất kỳ
Trường hợp này là trường hợp tổng quát nhất, hàm số ở đây có thể là hàm đa thức, phân thức, lượng giác, số mũ, Logarit, …
Cách giải chung cho trường hợp này là sử dụng Cách 1 của Trường hợp 1 nhé các bạn !
Lời kết
Okay, đó là những cách viết phương trình đường thẳng đi qua hai điểm cực trị mà mình muốn chia sẻ với các bạn trong bài viết này.
Nói tóm lại là:
Khi được yêu cầu viết phương trình đường thẳng đi qua 2 điểm cực trị thì đầu tiên, bạn hãy quan sát hàm số có rơi vào Trường hợp 1 hoặc Trường hợp 2 hay không
Nếu có thì bạn hãy áp dụng Cách 2 của Trường hợp 1, hoặc là công thức tính nhanh của Trường hợp 2 để tiết kiệm thời gian và công sức giải bài tập nhé.
Nếu không may rơi vào Trường hợp 3, hoặc bạn không nhớ công thức tính nhanh thì bạn hãy áp dụng Cách 1 của Trường hợp 1 ha.
Bởi như mình đã nói bên trên, cách này tuy là tốn khá nhiều thời gian nhưng đây là cách tổng quát nhất, giải được mọi trường hợp cho mọi hàm số. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
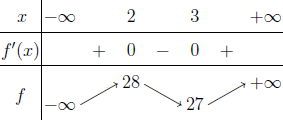





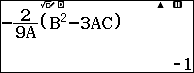



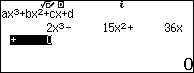
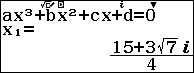
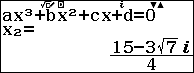
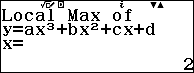

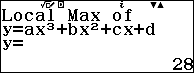

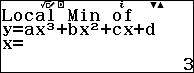

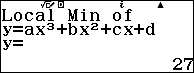


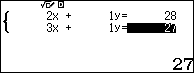







Cho em hỏi là khi người ta Cho hình vẽ đồ thị của hàm bậc 3 và tìm phương trình đường thẳng qua 2 điểm cực trị thì làm thế nào ạ?