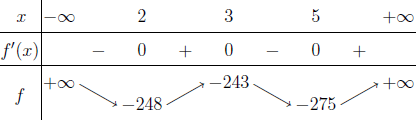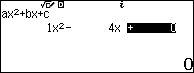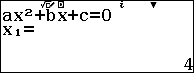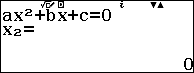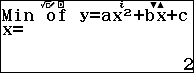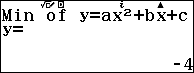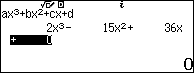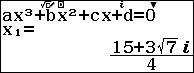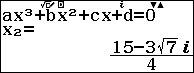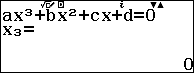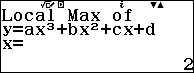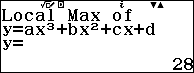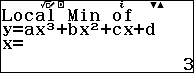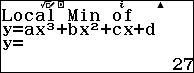Tìm cực trị của hàm số là một trong những bài toán cơ bản nhất của Giải tích cổ điển và rất thường gặp trong các bài kiểm tra, bài thi và đặc biệt là trong Kỳ thi Trung học Phổ thông Quốc gia
Vậy nên trong bài viết ngày hôm nay mình sẽ hướng dẫn các bạn cách tìm cực trị của hàm số đa thức, đa thức ở đây là đa thức một biến các bạn nhé.
Sở dĩ mình chọn hàm đa thức vì hàm đa thức là hàm số thường gặp nhất trong các hàm số Toán học. Okay, chúng ta bắt đầu thôi nào !
Mục Lục Nội Dung
I. Hàm số đa thức là gì?
Hàm số có dạng $f(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-2}x^{n-2}+a_{n-1}x^{n-1}+a_nx^n$ với $a_0, a_2, a_3, \dots a_n$ là những số thực cho trước. Trong đó, n là một số tự nhiên khác 0 được gọi là hàm số đa thức.
Ví dụ. $f(x)=2x+3, g(x)=2x^2+3x+5, h(x)=2x^3+3x^2+5x+7$ là những hàm đa thức.
II. Làm thế nào để tìm cực trị của hàm số đa thức?
Có khá nhiều cách để tìm cựu trị của hàm số đa thức và bên dưới là 3 cách đơn giản nhất kèm ví dụ minh họa cho các bạn dễ hình dung hơn.
#1. Sử dụng phương pháp Toán học
Đây là phương pháp chủ yếu để tìm cực trị của hàm số đa thức và cả những hàm số khác như hàm phân thức, hàm lượng giác, hàm logarit, …
Cách #1. Dựa vào bảng biến thiên
Bước 1. Tìm tập xác định của hàm số (ở đây mình chỉ xét các hàm đa thức nên tập xác định luôn luôn là R)
Bước 2. Tính $f’(x)$
Bước 3. Giải phương trình $f’(x)=0$ (vì tập xác định là R nên không có điểm nào làm cho $f’(x)$ không xác định)
Bước 4. Lập bảng biến thiên
Bước 5. Suy ra các điểm cực trị
Ví dụ 1. Tìm cực trị của hàm số $f(x)=3x^4-40x^3+186x^2-360x$
Lời giải:
Vì f(x) là hàm đa thức nên có tập xác định là R
$f’(x)=12(-30+31x-10x^2+x^3)$
$f’(x)=0 \Leftrightarrow 12(-30+31x-10x^2+x^3)=0 \Leftrightarrow 12(x – 5)(x – 3)(x – 2)=0$
Suy ra $x=2, x=3, x=5$ là nghiệm của phương trình $f’(x)=0$
Suy ra hàm số có ba điểm cực trị, cụ thể …
Cách 1:
- $x=2$ và $x=5$ là hai điểm cực tiểu của hàm số.
- $x=3$ là điểm cực đại của hàm số.
Cách 2:
- $(2; -248)$ và $(5; -275)$ là hai điểm cực tiểu của đồ thị hàm số.
- $(3; -243)$ là điểm cực đại của đồ thị hàm số.
Chú ý:
- Nếu là tự luận thì bạn có thể kết luận bằng Cách 1 hoặc Cách 2.
- Nếu là trắc nghiệm thì bạn cần xem kỹ đề hỏi cái gì để trả lời cho chính xác nhé.
Cách #2. Dựa vào đạo hàm cấp hai
Bước 1. Tìm tập xác định của hàm số (ở đây mình chỉ xét các hàm đa thức nên tập xác định luôn luôn là R)
Bước 2. Tính $f’(x)$
Bước 3. Giải phương trình $f’(x)=0$. Giả sử $x_i$ với $(i=1, 2, 3, \cdots, n)$ là các nghiệm vừa tìm được
Bước 4. Tính $f’’(x)$
Bước 5. Tính $f’’(x_i)$ và dựa vào dấu của $f’’(x_i)$ suy ra tính chất cực trị của điểm $x_i$
Ví dụ 2. Tìm cực trị của hàm số $f(x)=3x^4-40x^3+186x^2-360x$
Lời giải:
Vì f(x) là hàm đa thức nên có tập xác định là R
$f’(x)=12(-30+31x-10x^2+x^3)$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
$f’(x)=0 \Leftrightarrow 12(-30+31x-10x^2+x^3)=0 \Leftrightarrow 12(x – 5)(x – 3)(x – 2)=0$
Suy ra $x=2, x=3, x=5$ là nghiệm của phương trình $f’(x)=0$
$f’’(x)=12(31-20x+3x^2)$
- $f’’(2)=36>0$ suy ra $x=2$ là điểm cực tiểu của hàm số.
- $f’’(3)=-24<0$ suy ra $x=3$ là điểm cực đại của hàm số.
- $f’’(5)=72>0$ suy ra $x=5$ là điểm cực tiểu của hàm số.
Suy ra hàm số có ba điểm cực trị, cụ thể …
Cách 1:
$x=2$ và $x=5$ là hai điểm cực tiểu của hàm số.
$x=3$ là điểm cực đại của hàm số.
Cách 2:
$(2; -248)$ và $(5; -275)$ là hai điểm cực tiểu của đồ thị hàm số.
$(3; -243)$ là điểm cực đại của đồ thị hàm số.
#3. Sử dụng máy tính CASIO để tìm cực trị của hàm số đa thức
Tính năng tìm cực trị của hàm số bậc hai và hàm số bậc ba là hai tính năng nguyên thủy của máy tính CASIO fx-580VN X (không phải thủ thuật) nên nó rất đơn giản và chính xác tuyệt đối.
Chú ý:
Máy tính CASIO fx-570ES Plus và CASIO fx-570VN Plus không hỗ trợ tính năng tìm cực trị của hàm số bậc ba.
3.1. Tìm hàm số đa thức bậc hai
Hàm số có dạng $f(x)=ax^2+bx+c$ với điều kiện $a \neq 0$ được gọi là hàm số đa thức bậc hai.
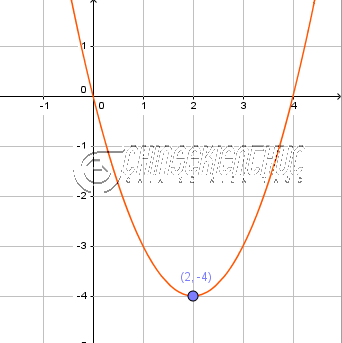
Ví dụ 3. Điểm cực tiểu của hàm số $x^2-4x$ là:
- A. 2
- B. -2
- C. (2; -4)
- D. (-2; -4)
Bước 1. Chọn phương thức tính toán Equation / Func
Bước 2. Chọn Polynomial
Bước 3. Chọn bậc của đa thức (vì bậc của đa thức là hai nên chúng ta sẽ nhấn phím số 2)
Bước 4. Nhập các hệ số …
Bước 5. Nhấn phím = => nhấn tiếp phím =
Sau khi nhấn phím = chúng ta sẽ thu được nghiệm của phương trình bậc hai tương ứng.
Bước 6. Nhấn phím = => nhấn phím =
Suy ra $x=2$ là điểm cực tiểu của hàm số hoặc $(2; -4)$ là điểm cực tiểu của đồ thị hàm số.
=> Vậy phương án A là đáp án !
Chú ý:
Nếu máy tính xuất hiện thông báo $Max~of~y=ax^2+bx+c$ thì đó là điểm cực đại.
3.2. Hàm số đa thức bậc ba
Hàm số có dạng $f(x)=ax^3+bx^2+cx+d$ với điều kiện $a \neq 0$ được gọi là hàm số đa thức bậc ba
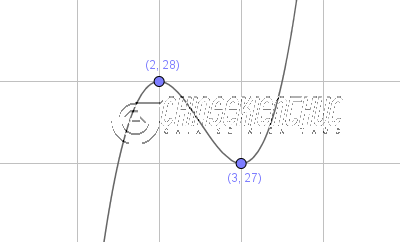
Ví dụ 4. Điểm cực đại của đồ thị hàm số $2x^3-15x^2+36x$
- A. (2; 28)
- B. 2
- C. (2; 28)
- D. 3
Bước 1. Chọn phương thức tính toán Equation / Func
Bước 2. Chọn Polynomial
Bước 3. Chọn bậc của đa thức (vì bậc của đa thức là ba nên chúng ta sẽ nhấn phím số 3)
Bước 4. Nhập các hệ số …
Bước 5. Nhấn phím = = > nhấn phím = => nhấn phím =
Sau khi nhấn phím = chúng ta sẽ thu được nghiệm của phương trình bậc ba tương ứng.
Bước 6. Nhấn phím = => nhấn phím = => nhấn phím = => nhấn phím =
Suy ra …
- $x=2$ là điểm cực đại của hàm số hoặc $(2; 28)$ là điểm cực đại của đồ thị hàm số.
- $x=3$ là điểm cực tiểu của hàm số hoặc $(3; 27)$ là điểm cực tiểu của đồ thị hàm số.
Vậy => phương án A là đáp án !
Chú ý:
- Số lần nhấn phím = với các hàm số bậc ba khác sẽ khác, bạn cần xem kỹ khi máy tính thông báo Local Max of hoặc Local Min of để kết luận cho chính xác.
- Nếu máy tính thông báo No Local Max / Min thì hàm số đã cho không có cực trị.
III. Lời kết
Okay, như vậy là qua bài viết này bạn đã biết cách rồi phải không?!
Trong mọi trường hợp mình luôn khuyến khích các bạn sử dụng phương pháp Toán học (mà cụ thể là Cách #1). Bởi cách 1 vừa chính xác, vừa phù hợp nhiều dạng hàm số, vừa rèn luyện kĩ năng lập bảng biến thiên, …
Phương pháp sử dụng máy tính CASIO chỉ nên áp dụng khi cần tìm cực trị của hàm số bậc hai / bậc ba và bài toán được cho dưới dạng trắc nghiệm.
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống