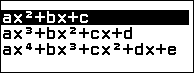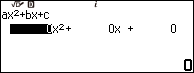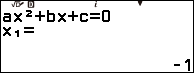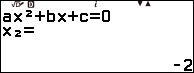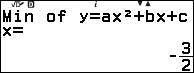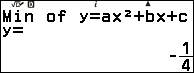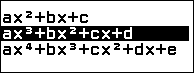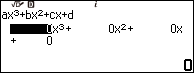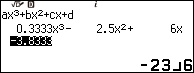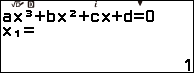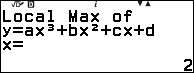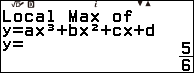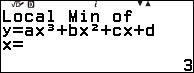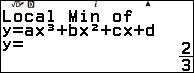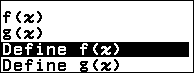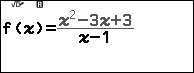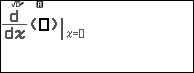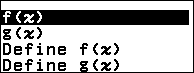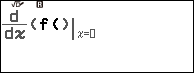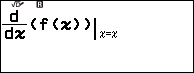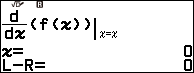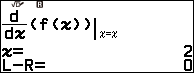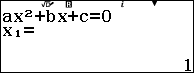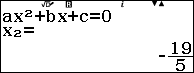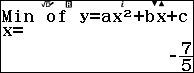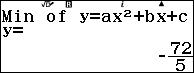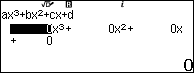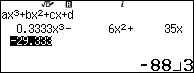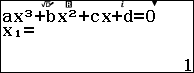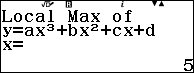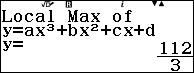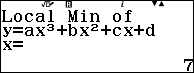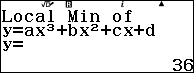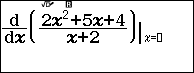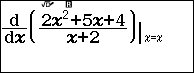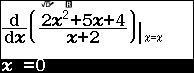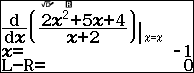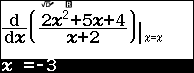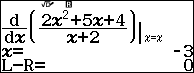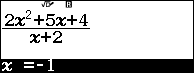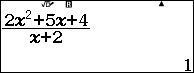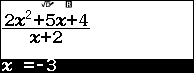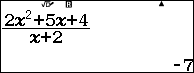Cách tìm cực trị của hàm số bằng máy tính Casio 580 & 880

Bạn đã biết cách tìm cực trị của hàm số bằng máy tính Casio chưa?

Thông thường, để tìm cực trị của một hàm số nào đó thì chúng ta thường sử dụng một trong các phương pháp sau đây:

• Phương pháp Toán học (lập bảng biến thiên, đạo hàm cấp hai).
• Phương pháp máy tính cầm tay (CASIO fx 880 BTG và fx 580 VN X).
• Phương pháp Tin học (dịch vụ giải toán trực tuyến Wolfram Alpha, phần mềm Maple),…

Vâng, nhưng trong khuôn khổ bài viết này mình sẽ tạm giác lại phương pháp Toán học và Tin học nhé các bạn.

Mà thay vào đó, mình sẽ hướng dẫn các bạn sử dụng máy tính CASIO để xác định nhanh cực trị của một số hàm số thường gặp.

Các hàm số được mình lựa chọn hướng dẫn cho các bạn là hàm số bậc hai $y=ax^2+bx+c$, hàm số bậc ba $y=ax^3+bx^2+cx+d$ và hàm số hàm phân thức hữu tỉ tam thức trên nhị thức $y=\frac{ax^2+bx+c}{a’x+b’}$ với $a \neq 0, a’ \neq 0$

#1. Cách tìm cực trị của hàm số trên Casio fx 880 BTG

NOTE:
Nếu chưa có máy tính Casio 880 BTG này thì bạn có thể đặt mua chính hãng tại đây hoặc tại đây !

Ví dụ 1. Xác định cực trị của hàm số bậc hai $y=x^2+3x+2$.

Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK

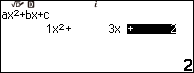
Bước 2. Nhập 1 => nhấn phím EXE => nhập 3 => nhấn phím EXE => nhập 2 => nhấn phím EXE

Bước 3. Nhấn phím EXE => nhấn phím EXE

Bước 4. Nhấn phím EXE => nhấn phím EXE

Vậy đồ thị hàm số đã cho có một điểm cực trị (cực tiểu) là $\left(-\frac{3}{2}, -\frac{1}{4}\right)$.

Chú ý:

• Nếu màn hình xuất hiện thông báo $Min~of~y=ax^2+bx+c$ thì điểm cực trị vừa tìm được là cực tiểu.
• Nếu màn hình xuất hiện thông báo $Max~of~y=ax^2+bx+c$ thì điểm cực trị vừa tìm được là cực đại.

Ví dụ 2. Xác định cực trị của hàm số bậc ba $y=\frac{1}{3}x^3-\frac{5}{2}x^2+6x-\frac{23}{6}$.

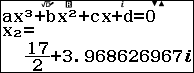
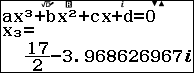
Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^3+bx^2+cx+d$ => nhấn phím OK

Bước 2. Nhập $\frac{1}{3}$ => nhấn phím EXE => nhập $-\frac{5}{2}$ => nhấn phím EXE => nhập 6 => nhấn phím EXE => nhập $-\frac{23}{6}$ => nhấn phím EXE

Bước 3. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE

Bước 4. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE => nhấn phím EXE

Vậy đồ thị hàm số đã cho có một điểm cực đại là $\left(2, \frac{5}{6}\right)$ và một điểm cực tiểu là $\left(3, \frac{2}{3}\right)$.

Chú ý:

• Nếu màn hình xuất hiện thông báo $Local~Min~of~y=ax^3+bx^2+cx+d$ thì điểm cực trị vừa tìm được là cực tiểu.
• Nếu màn hình xuất hiện thông báo $Local~Max~of~y=ax^3+bx^2+cx+d$ thì điểm cực trị vừa tìm được là cực đại.
• Nếu màn hình xuất hiện thông báo No Local Max / Min thì hàm số đã cho không có cực trị.

Ví dụ 3. Xác định cực trị của hàm số hàm phân thức hữu tỉ tam thức trên nhị thức $y=\frac{x^2-3x+3}{x-1}$.

Bước 1. Nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK => nhập $\frac{x^2-3x+3}{x-1}$ => nhấn phím EXE

Bước 2.

Bước 2.1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK

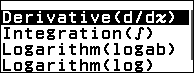
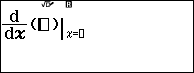
Bước 2.2. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

Bước 2.3. Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK

Bước 2.4. Nhấn phím x => nhấn phím ) => nhấn phím SHIFT => nhấn phím  => nhấn phím x

Bước 2.5. Nhấn phím EXE => nhấn phím   => nhấn phím EXE

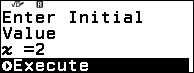
Bước 3. Nhấn phím EXE => nhấn phím EXE => nhập $2 \times \left(-\frac{-1}{1}\right)-0$ => nhấn phím EXE => nhấn phím EXE

Chú ý:
Giá trị x ban đầu là để tìm được hoành độ của điểm cực trị của hàm số $y=\frac{ax^2+bx+c}{a’x+b’}$ là $2 \times (-\frac{b’}{a’}) – x_1$ với $x_1$ là nghiệm của phương trình $y’=0$.

Bước 4.

Bước 4.1. Nhấn phím HOME => chọn Calculate => nhấn phím OK

Bước 4.2. Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập 0 => nhấn phím EXE

Bước 4.3. Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập 2 => nhấn phím EXE

Vậy tọa độ các điểm cực trị của hàm số đã cho là (0, -3) và (2, 1).

Xem video bấm máy Casio fx 880 BTG

#2. Cách tìm cực trị của hàm số trên Casio fx 580 VN X

NOTE:
Nếu chưa có máy tính Casio 580 VNX này thì bạn có thể đặt mua chính hãng tại đây nhé !

Ví dụ 4. Xác định cực trị của hàm số bậc hai $y=\frac{5}{2}x^2+7x-\frac{19}{2}$.

Bước 1. Nhấn phím MENU => chọn Equation / Func => nhấn phím  => nhấn phím 2 để chọn Polynomial => nhập 2 để khai báo bậc của hàm số.

Bước 2. Nhập $\frac{5}{7}$ => nhấn phím EXE => nhập 7 => nhấn phím EXE => nhập $-\frac{19}{2}$ => nhấn phím EXE

Bước 3. Nhấn phím EXE => nhấn phím EXE

Bước 4. Nhấn phím EXE => nhấn phím EXE

Vậy đồ thị hàm số đã cho có một điểm cực trị (cực tiểu) là $\left(-\frac{7}{5}, -\frac{72}{5}\right)$.

Ví dụ 5. Xác định điểm cực trị của hàm số bậc ba $y=\frac{1}{3}x^3-6x^2+35x-\frac{88}{3}$.

Bước 1. Nhấn phím MENU => chọn Equation / Func => nhấn phím  => nhấn phím 2 để chọn Polynomial => nhập 3 để khai báo bậc của hàm số

Bước 2. Nhập $\frac{1}{3}$ => nhấn phím EXE => nhập -6 => nhấn phím EXE => nhập 35 => nhấn phím EXE => nhập $-\frac{88}{3}$ => nhấn phím EXE

Bước 3. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE

Bước 4. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE => nhấn phím EXE

Vậy đồ thị hàm số đã cho có một điểm cực đại là $\left(5, \frac{112}{3}\right)$ và một điểm cực tiểu là (7, 36).

Ví dụ 6. Xác định cực trị của hàm số hàm phân thức hữu tỉ tam thức trên nhị thức $y=\frac{2x^2+5x+4}{x+2}$.

Bước 1. Nhấn phím SHIFT => nhấn phím  => nhập $\frac{2x^2+5x+4}{x+2}$ => nhấn phím SHIFT => nhấn phím  => nhấn phím SHIFT => nhấn phím  => nhập x

Bước 2. Nhấn phím SHIFT => nhấn phím CALC => nhập giá trị x ban đầu là 0 => nhấn phím => nhấn phím

Bước 3. Nhấn phím SHIFT => nhấn phím CALC => nhập giá trị x ban đầu là $2 \times \left(-\frac{2}{1}\right)–1$ => nhấn phím => nhấn phím

Chú ý:
Giá trị x ban đầu là để tìm được hoành độ của điểm cực trị của hàm số $y=\frac{ax^2+bx+c}{a’x+b’}$ là $2 \times (-\frac{b’}{a’}) – x_1$ với $x_1$ là nghiệm của phương trình $y’=0$

Bước 4. Nhập $\frac{2x^2+5x+4}{x+2}$

Bước 5.

Bước 5.1. Nhấn phím CALC => nhập -1 => nhấn phím =

Bước 5.2. Nhấn phím CALC => nhập -3 => nhấn phím =

Vậy tọa độ các điểm cực trị của hàm số đã cho là (-1, 1) và (-3, -7)

Xem video bấm máy Casio fx 580 VNX

#3. Lời kết

Vâng, trên đây là chi tiết các bước tìm cực trị của ba hàm số thường gặp nhất bằng máy tính CASIO fx 580 VNX và 880 BTG..

Các hàm số khác vẫn tìm được bằng máy tính CASIO nhưng có phần phức tạp hơn, tạm thời mình chưa thể hướng dẫn cho các bạn.

Hi vọng  bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

Đọc thêm:

• Dùng Casio để chuyển từ độ sang radian (radian sang độ)
• Cách tính Sin, Cos, Tan, Cot trên máy tính Casio 580 và 880
• Dùng CASIO chuyển số thập phân vô hạn tuần hoàn ra phân số và ngược lại

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn