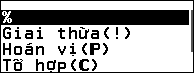
Hoán vị, chỉnh hợp và tổ hợp là một trong những kiến thức bắt buộc phải nằm vững nếu bạn muốn học tốt học phần xác suất.
Nói về hoán vị, chỉnh hợp và tổ hợp thì có nhiều mảng kiến thức cần phải nắm vững, tuy nhiên trong phạm vi ngắn gọn của bài viết này chúng ta sẽ chỉ tập trung nhiều vào cách tính.
Và dưới đây là chi tiết các bước để tính hoán vị, chỉnh hợp và tổ hợp bằng máy tính CASIO fx 880 BTG và Casio fx 580 VN.
Mục Lục Nội Dung
#1. Hoán vị, chỉnh hợp và tổ hợp là gì?
Cho tập hợp A gồm n phần tử với n khác 1
+) Mỗi kết quả của sự sắp xếp thứ tự n phần tử của A được gọi là một hoán vị của n phần tử đó và được tính theo công thức $P_n=n(n-1)(n-2) \dots 3.2.1$
+) Kết quả của việc lấy k phần tử khác nhau từ n phần tử của A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho và được tính theo công $A_n^k= n(n-1)(n-2)(n-3) \cdots (n-k+1)=\frac{n!}{(n-k)!}$
+) Mỗi tập hợp con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử và được tính theo công thức $C_n^k=\frac{n!}{k!(n-k)!}$
Nếu bạn muốn tìm hiểu kỹ hơn về khái niệm của Hoán vị, Chỉnh hợp và Tổ hợp thì bạn có thể đọc thêm các định nghĩa sau đây:
1.1. Hoán vị là gì?
Hoán vị được sử dụng để mô tả số lượng các cách khác nhau mà một tập hợp các phần tử có thể được sắp xếp theo một thứ tự nhất định.
Trong đó, hoán vị của một tập hợp gồm n phần tử được ký hiệu là n! (n giai thừa) và tính bằng tích của tất cả các số nguyên dương từ 1 đến n.
Ví dụ, hoán vị của tập hợp {1, 2, 3} là 3! = 6, bao gồm các cách sắp xếp sau:
- 1 2 3
- 1 3 2
- 2 1 3
- 2 3 1
- 3 1 2
- 3 2 1
Các hoán vị có thể được áp dụng trong nhiều lĩnh vực, như lý thuyết xác suất, thống kê, mã hóa thông tin, và tối ưu hóa.
1.2. Chỉnh hợp là gì?
Chỉnh hợp là một khái niệm trong toán học để mô tả số lượng cách khác nhau mà một tập hợp các phần tử có thể được chọn ra và sắp xếp trong một thứ tự nhất định.
Cụ thể thì, chỉnh hợp của một tập hợp gồm n phần tử, được ký hiệu là A(n,k), là số lượng cách chọn k phần tử từ n phần tử và sắp xếp chúng theo một thứ tự nhất định.
Chỉnh hợp được tính bằng công thức: A(n,k) = n! / (n-k)!
Ví dụ, nếu chúng ta có một tập hợp {1, 2, 3, 4} và muốn chọn ra 2 phần tử và sắp xếp chúng theo một thứ tự nhất định, ta có thể tính chỉnh hợp như sau:
A(4,2) = 4! / (4-2)! = 12
Có 12 cách chọn và sắp xếp 2 phần tử từ tập hợp {1, 2, 3, 4}, bao gồm các cặp số sau:
1 2, 1 3, 1 4, 2 1, 2 3, 2 4, 3 1, 3 2, 3 4, 4 1, 4 2, 4 3
Các chỉnh hợp có thể được sử dụng trong nhiều lĩnh vực, như lý thuyết xác suất, thống kê, và kỹ thuật tính toán.
1.3. Tổ hợp là gì?
Tổ hợp được sử dụng để mô tả số lượng các cách khác nhau mà một tập hợp các phần tử có thể được chọn ra từ một tập hợp lớn hơn, mà không cần quan tâm đến thứ tự của các phần tử được chọn.
Cụ thể hơn thì, tổ hợp của một tập hợp gồm n phần tử được ký hiệu là C(n,k) hoặc nCk, là số lượng cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự.
Tổ hợp được tính bằng công thức: C(n,k) = n! / (k! * (n-k)!)
Ví dụ, nếu chúng ta có một tập hợp {1, 2, 3, 4} và muốn chọn ra 2 phần tử mà không quan tâm đến thứ tự, ta có thể tính tổ hợp như sau:
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
C(4,2) = 4! / (2! * (4-2)!) = 6
Có 6 cách chọn 2 phần tử từ tập hợp {1, 2, 3, 4} mà không quan tâm đến thứ tự, bao gồm các cặp số sau:
- 1 2
- 1 3
- 1 4
- 2 3
- 2 4
- 3 4
Các tổ hợp có thể được sử dụng trong nhiều lĩnh vực, như lý thuyết xác suất, thống kê, kỹ thuật tính toán, và tối ưu hóa.
#2. Thực hành tính trên Casio fx 880 BTG
NOTE:
Nếu chưa có máy tính Casio này thì bạn có thể đặt mua chính hãng tại đây hoặc tại đây !
Ví dụ 1. Tính số các hoán vị của 13
Bước 1. Nhập 13
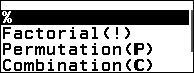
Bước 2. Nhấn phím CATALOG => chọn Probability => nhấn phím OK => chọn Factorial (!) => nhấn phím OK

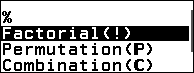
Bước 3. Nhấn phím EXE
Vậy số các hoán vị của 13 là 6 227 020 800
Chú ý:
Tính năng Factorial (!) của máy tính Casio fx 880 BTG chỉ cho phép chúng ta tính tối ta là 69!
Ví dụ 2. Tính số các chỉnh hợp chập 9 của 13
Bước 1. Nhập 13
Bước 2. Nhấn phím CATALOG => chọn Probability => nhấn phím OK => chọn Permutation (P) => nhấn phím OK
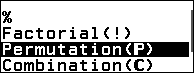
Bước 3. Nhập 9
Bước 4. Nhấn phím EXE
Vậy số các chỉnh hợp chập 9 của 13 là 259 459 200
Chú ý:
Sách giáo khoa thường kí hiệu chỉnh hợp chập k của n phần tử là $A_n^k$ còn fx 880 BTG là nPk
Ví dụ 3. Tính số các tổ hợp chập 14 của 16
Bước 1. Nhập 16
Bước 2. Nhấn phím CATALOG => chọn Probability => nhấn phím OK => chọn Combination (C) => nhấn phím OK
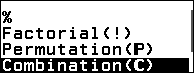
Bước 3. Nhập 14
Bước 4. Nhấn phím EXE
Vậy số các tổ hợp chập 14 của 16 là 120
Chú ý:
Sách giáo khoa thường kí hiệu tổ hợp chập k của n phần tử là $C_n^k$ còn fx 880 BTG là nCk
Xem video hướng dẫn
#3. Thực hành tính trên Casio fx 580 VN X
Đọc thêm:
Đặt mua CASIO FX-580 VNX chính hãng
Giả lập máy tính CASIO FX-580 VNX trên điện thoại, máy tính
Ví dụ 1. Tính số các hoán vị của 11
Bước 1. Nhập 11
Bước 2. Nhấn phím SHIFT => nhấn phím
Bước 3. Nhấn phím =
Vậy số các hoán vị của 11 là 39 916 800
Ví dụ 2. Tính số các chỉnh hợp chập 5 của 9
Bước 1. Nhập 9
Bước 2. Nhấn phím SHIFT => nhấn phím
Bước 3. Nhập 5
Bước 4. Nhấn phím =
Vậy số các chỉnh hợp chập 5 của 9 là 15 120
Ví dụ 3. Tính số các tổ hợp chập 4 của 50
Bước 1. Nhập 50
Bước 2. Nhấn phím SHIFT => nhấn phím
Bước 3. Nhập 4
Bước 4. Nhấn phím =
Vậy số các tổ hợp chập 4 của 50 là 230 300
Xem video hướng dẫn
#4. Các bạn hãy thận trọng khi sử dụng máy tính Casio giao diện tiếng Việt
Casio fx 880 BTG được sản xuất hướng đến người dùng Việt Nam nên có giao diện tiếng Việt.
Mặc dù việc sử dụng giao diện tiếng Việt mang lại cho chúng ta một số lợi ích nhất định nhưng nó cũng có một số nhược điểm.
Nhược điểm dễ thấy nhất là sai sót khi dịch Permutation là Hoán vị, dịch như vậy là chưa chính xác, chính xác phải là chỉnh hợp.
#5. Lời kết
Vâng, trên đây là cách bấm máy tính để tính hoán vị, chỉnh hợp và tổ hợp bằng máy tính Casio.
Và như các bạn có thể thấy, việc tính hoán vị, chỉnh hợp và tổ hợp bằng máy tính CASIO cũng không có gì khó khăn cả đúng không ạ.
Bạn chỉ cần nhớ chính xác công dụng của từng tính năng là được, đặc biệt là tính năng Permutation (P) và Combination (C).
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống