Công thức tính hoán vị, chỉnh hợp và tổ hợp đầy đủ

Xin chào tất cả các bạn !

Hôm nay, chúng ta sẽ cùng nhau ôn lại các công thức tính số các hoán vị, chỉnh hợp và tổ hợp ha.

Ngoài ra thì mình cũng hướng dẫn thêm cho bạn cách tính số các hoán vị, chỉnh hợp và tổ hợp bằng máy tính cầm tay CASIO FX 580 VNX

#1.Quy tắc đếm

Để đếm được số phần tử của một tập hợp hữu hạn nào đó chúng ta thường phải sử dụng quy tắc cộng và quy tắc nhân.

Không ít tập hợp hữu hạn rất khó xác định được số phần tử của chúng nếu không sử dụng hai quy tắc trên.

Tuy đây không phải là nội dung chính của bài viết nhưng nó là tiền đề để chúng ta  có thể dễ dàng tiếp cận các kiến thức về hoán vị, chính vị và tổ hợp.

1.1. Quy tắc cộng

Một công việc được thực hiện theo hai phương án $X$ và $Y$

Nếu phương án $X$ có $m$ cách thực hiện, phương án $Y$ có $n$ cách thực hiện và không trùng với bất kỳ cách nào của phương án $X$ thì công việc đó có $m+n$ cách thực hiện.

Nếu $A$ và $B$ là hai tập hợp hữu hạn không giao nhau thì $n(A \cup B)=n(A) + n(B)$

Nếu $A$ và $B$ là hai tập hợp hữu hạn bất kỳ thì $n(A \cup B)=n(A) + n(B) – n(A \cap B)$

Trường hợp tổng quát:

Nếu $A_1, A_2, A_3, \dots, A_n$ là các tập hợp hữu hạn và đôi một không giao nhau thì $n(A_1 \cup A_2 \cup A_3 \cup \cdots \cup A_n)=n(A_1)+n(A_2)+n(A_3) + \cdots + n(A_n)$

1.2. Quy tắc nhân

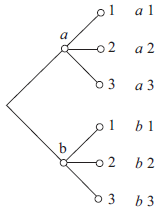
Một công việc được hoàn thành bởi hai gian đoạn liên tiếp $X$ và $Y$

Nếu giai đoạn $X$ có $m$ cách thực hiện và ứng với mỗi cách đó có $n$ cách thực hiện ở giai đoạn $Y$ thì có $mn$ cách hoàn thành công việc.

Quy tắc nhân có thể mở rộng cho công việc có nhiều giai đoạn liên tiếp.

#2. Cách tính Hoán vị

Cho tập hợp $A$ có $n$ phần tử ($n$ lớn hơn hoặc bằng $1$)

Mỗi kết quả của sự sắp xếp $n$ phần tử của tập hợp $A$ theo một thứ tự nào đó được gọi là một hoàn vị của $n$ phần tử đã cho.

Ký hiệu số các hoán vị của $n$ phần tử là $P_n$

Lúc này, $P_n$ sẽ bằng $n!$ hoặc $n(n-1)(n-2)(n-3) \dots 2 \dot{} 1$

Để tính số các hoán vị của $n$ phần tử bằng máy tính cầm tay CASIO fx 580 VN X thì bạn hãy nhập $n$ => nhấn rồi nhấn phím  => nhấn phím

Ví dụ 1.

Chẳng hạn mình cần tính số các hoàn vị của $9$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1. Nhập $9$

Bước 2. Nhấn rồi nhấn phím

Bước 3. Nhấn phím

Vậy số các hoán vị của $9$ là $362880$

#3. Cách tính Chỉnh hợp

Cho tập hợp $A$ có $n$ phần tử ($n$ lớn hơn hoặc bằng $1$)

Mỗi kết quả của việc lấy $k$ phần tử từ $n$ phần tử của tập hợp $A$  ($1 \leq k \leq n$) và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập $k$ của $n$ phần tử

Ký hiệu số các chỉnh hợp chập $k$ của $n$ phần tử là $A_n^k$

Lúc này $A_n^k$ sẽ bằng $n(n-1)(n-2)(n-3) \cdots (n-k+1)$

Vì $A_n^n=n!=P_n$ và $0!=1$ và $A_n^0=1$ nên với $0 \leq k \leq n$ chúng ta có $A_n^k=\frac{n!}{(n-k)!}$

Để tính số các chỉnh hợp chập $k$ của $n$ phần tử tính bằng máy tính cầm tay CASIO FX 580 VN X thì bạn hãy nhập $n$ => nhấn rồi nhấn phím   => nhập $k$ => nhấn phím

Ví dụ 2.

Chẳng hạn mình cần tính số các chỉnh hợp chập $2$ của $9$ thì thực hiện tuần tự theo các bước bên dưới:

Bước 1. Nhập $9$

Bước 2. Nhấn rồi nhấn phím

Bước 3. Nhập $2$

Bước 4. Nhấn phím

Vậy số các chỉnh hợp chập $2$ của $9$ bằng $72$

#4. Cách tính Tổ hợp

Cho tập hợp $A$ gồm $n$ phần tử ($n$ lớn hơn hoặc bằng $1$)

Mỗi tập con gồm $k$ phần tử của $A$ được gọi là một tổ hợp chập $k$ của $n$ phần tử.

Ký hiệu số các tổ hợp chập $k$ của $n$ phần tử là $C_n^k$

Lúc này $C_n^k$ sẽ bằng $\frac{A_n^k}{k!}$ hoặc $\frac{ n(n-1)(n-2)(n-3) \cdots (n-k+1)}{k!}$

Vì $C_n^0=1$ nên các công thức trên cũng đúng với $0 \leq k \leq n$ và lúc bấy giờ chúng ta có công thức $C_n^k=\frac{n!}{k!(n-k)!}$

Một vài tính chất cơ bản của tổ hợp:

$C_n^k=C_n^{n-k}$ với $n, k$ tự nhiên và $0 \leq k \leq n$

$C_{n+1}^k=C_n^{k+1}+C_n^k$ với $1 \leq k \leq n$

Để tính số các tổ hợp chập $k$ của $n$ bằng máy tính cầm tay CASIO fx 580 VN X thì bạn hãy nhập $n$ => nhấn  rồi nhấn phím => nhập $k$ => nhấn phím

Ví dụ 3.

Để hạn mình cần tính số các tổ hợp chập $2$ của $9$ thì thực hiện theo các bước bên dưới

Bước 1. Nhập $9$

Bước 2. Nhấn  rồi nhấn phím

Bước 3. Nhập $2$

Bước 4. Nhấn phím

Vậy số các tổ hợp chập $2$ của $9$ bằng $36$

#5. Lời kết

Quy tắc cộng, quy tắc nhân, hoán vị, chỉnh hợp và tổ hợp là các kiến cơ bản nhất về Đại số tổ hợp.

Đây chính là chìa khóa để chúng ta có thể tiếp cận Lý thuyết xác suất, một lĩnh vực quan trọng và có nhiều ứng dụng của Toán học cũng như trong thực tiễn.

Vậy nên bạn hãy học kỹ phần này nhé các bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

• Công thức lũy thừa, khai căn và Lôgarit đáng nhớ
• 10 công thức tính vi phân của các hàm số thường gặp

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn