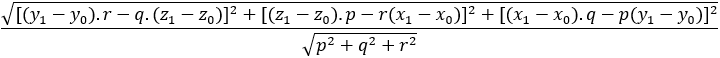2 cách tính khoảng cách từ một điểm đến một đường thẳng

Nếu như việc tính khoảng cách từ một điểm đến một đường thẳng nằm trên mặt phẳng không có gì khó khăn thì việc tính khoảng cách từ một điểm đến một đường thẳng nằm trong không gian lại khá là phức tạp.

Thông thường bạn sẽ cần thực hiện các bước sau:

Viết phương trình đường thẳng đi qua điểm đã cho và vuông góc với đường thẳng đã cho, tiếp theo tìm giao điểm của đường thẳng vừa viết và đường thẳng đã cho, và cuối cùng là tính khoảng cách giữa giao điểm vừa tìm được với điểm đã cho.

Các bước trên dù không quá phức tạp nhưng nó cũng tốn khá nhiều thời gian và công sức, đặc biệt vì tính toán khá nhiều nên dễ xảy ra sai sót.

Vậy nên hôm nay, mình sẽ hướng dẫn các bạn cách tính khoảng cách từ một điểm đến một đường thẳng trong không gian bằng một cách khác dễ dàng hơn khá nhiều. Cách này chủ yếu dựa vào tích có hướng hoặc máy tính CASIO fx-580VN X.

I. Trường hợp: Điểm và đường thẳng nằm trên mặt phẳng

Đọc thêm:

• Cách giả lập máy tính CASIO FX-580 VNX trên Windows
• Cách tạo phím bấm của Casio fx-580VN X trên Word và LaTeX

#1. Công thức tính khoảng cách từ một điểm đến một đường thẳng

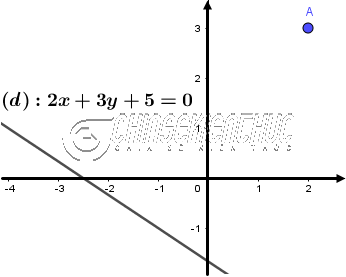
Tính khoảng cách từ điểm $M_1$ và đường thẳng $(d)$ biết $M_1=(x_1; y_1)$ và đường thẳng $(d): Ax+By+C=0$

$(M_1; (d))=\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$

#2. Ví dụ minh họa

Tính khoảng cách từ điểm $A=(2; 3)$ đến đường thẳng $(d): 2x+3y+5=0$[/toggle]

Lời Giải:

Áp dụng công thức $\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$ ta được $\frac{|2.2+3.3+5|}{\sqrt{2^2+3^2}}=\frac{18\sqrt{13}}{13} \approx 5$

=> Vậy khoảng cách từ điểm $A=(2; 3)$ đến đường thẳng $(d): 2x+3y+5=0$ gần bằng 5 ĐVĐD

II. Trường hợp: Điểm và đường thẳng nằm trong không gian

#1. Cách tính khoảng cách từ một điểm đến một đường thẳng

Tính khoảng cách từ điểm $M_1=(x_1; y_1; z_1)$ đến đường thẳng $(d): \frac{x-x_0}{p}=\frac{y-y_0}{q}=\frac{z-z_0}{r}$

$\frac{\sqrt{[(y_{1}-y_{0}).r-q.(z_{1}-z_{0})]^{2}+[(z_{1}-z_{0}).p-r(x_{1}-x_{0})]^{2}+[(x_{1}-x_{0}).q-p(y_{1}-y_{0})]^{2}}}{\sqrt{p^2+q^2+r^2}}$

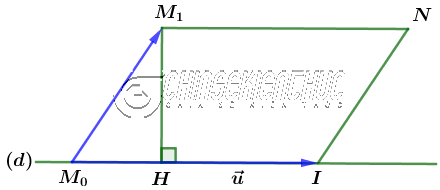
#2. Cách chứng minh

Dễ thấy đường thẳng $(d)$ đi qua điểm $M_0=(x_0; y_0; z_0)$ và có véc-tơ chỉ phương $\vec{u}=(p; q; r)$

$\overrightarrow{M_0M_1}$ và $\vec{u}= \overrightarrow{M_0I}$ tạo thành một hình bình hành có diện tích S

$h=M_1H=\frac{S}{|\overrightarrow{M_0I}|}=\frac{|[\overrightarrow{M_0M_1}; \vec{u}]|}{|\vec{u}|}$

#3. Ví dụ minh họa

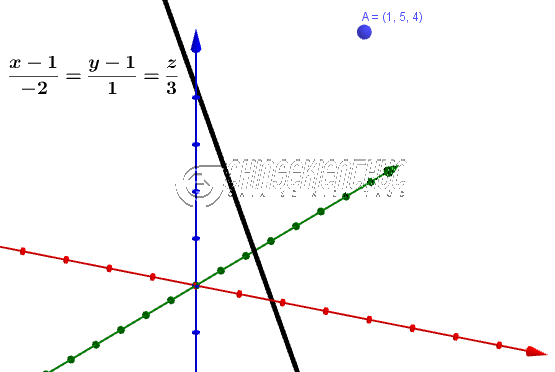
Tính khoảng cách từ điểm $A=(1; 5; 4)$ đến đường thẳng $(d):\frac{x-1}{-2}=\frac{y-1}{1}=\frac{z}{3}$

Lời Giải:

Dễ thấy đường thẳng $(d)$ đi qua điểm $M_0=(1; 1; 0)$ và có véc-tơ chỉ phương $\vec{u}=(-2; 1; 3)$

Suy ra $\overrightarrow{M_0A}=(0; 4; 4)$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Tích có hướng của $\overrightarrow{M_0A}$ và $\vec{u}$ bằng $(8; -8; 8)$

Độ dài tích có hướng của $\overrightarrow{M_0A}$ và $\vec{u}$ bằng $\sqrt{(8)^2+(-8)^2+(8)^2}=8\sqrt{3}$

Độ dài $\vec{u}$ bằng $\sqrt{(-2)^2+(1)^2+(3)^2}=\sqrt{14}$

=> Vậy khoảng cách từ điểm $A$ đến đường thẳng $(d)$ là $\frac{8\sqrt{3}}{\sqrt{14}}= \frac{4\sqrt{42}}{7}\approx 3.7$

#4. Cách tính khoảng cách từ một điểm đến một đường thẳng bằng CASIO

//Bài viết này mình sẽ sử dụng Casio fx 580 VNX các bạn nhé !

Bước 1. Chọn phương thức tính toán Vector

Bước 2. Lần lượt gán $\overrightarrow{M_0A}, \vec{u}$ cho VctA, VctB

Bước 3. Tích tích có hướng của $\overrightarrow{M_0A}$ và $\vec{u}$

Bước 4. Tính khoảng cách theo công thức (Abs(VctAns))⨼(Abs(VctB))

III. Lời kết

Công thức tính khoảng cách từ một điểm đến một đường thẳng nằm trong không gian (ý mình là tính trực tiếp ý) tuy là có, nhưng quá phức tạp và rất khó nhớ. Bạn chỉ có thể nhớ được khi bạn có trí nhớ rất rất tốt.

Vậy nên thay vì cố gắng nhớ một cách máy móc bạn hãy xem phần #2 trong mục II (cách chứng minh) để biết cách mà mình đã dùng để xây dựng công thức, từ đó việc ghi nhớ công thức cũng dễ dàng hơn.

Trong quá trình áp dụng nếu là …

• Tự luận thì bạn có thể dựa vào nội dung trong mục con phần #2 trong mục II (cách chứng minh) hoặc phần #3 trong mục II (ví dụ minh họa) để trình bày theo.
• Trắc nghiệm thì bạn hãy áp dụng công thức hoặc thủ thuật tính nhanh bằng máy tính CASIO fx-580VN X nhé.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách sử dụng phần mềm Toán học MathType
• Cách tạo bài giảng điện tử, bài giảng E-Learning chuyên nghiệp

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn