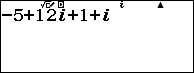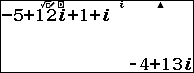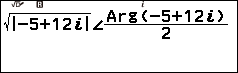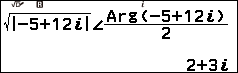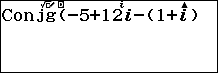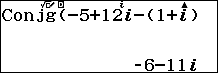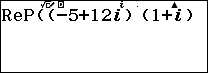Tính năng Complex của máy tính Casio fx 880 BTG là một trong những tính năng được sử dụng thường xuyên nhất.
Tính năng này cho phép chúng ta nhập các số phức và thực hiện các thao tác tính toán với chúng một cách vô cùng nhanh chóng và thuận tiện.
Các thao tác tính toán được hỗ trợ là các phép tính số học (cộng, trừ, nhân, chia), lũy thừa, khai căn bậc hai, acgumen, số phức liên hợp, phần thực / phần ảo, môđun, chuyển đổi số phức từ dạng đại số sang dạng lượng giác, …
Vâng, và trong bài viết này mình sẽ hướng dẫn chi tiết cho A/C/E cách sử dụng máy tính Casio 880 BTG để tính toán số phức một cách dễ hiểu nhất.
Chú ý:
Môi trường số phức trên máy tính Casio fx 880 BTG không còn hỗ trợ tính năng CALC.
Mục Lục Nội Dung
#1. Hướng dẫn tính số phức trên Casio fx 880 BTG
NOTE:
Nếu chưa có máy tính Casio 880 BTG này thì bạn có thể đặt mua chính hãng tại đây hoặc tại đây !
Đề bài:
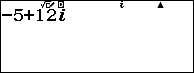
Cho $z_1=-5+12i$ và $z_2=1+i$ hãy thực hiện theo các yêu cầu được liệt kê bên dưới:
- a) Tính $z_1+z_2$
- b) Tính $z_1^2$
- c) Khai căn bậc hai của $z_1$
- d) Tính acgumen của $z_2$
- e) Xác định số phức liên hợp của $z_1-z_2$
- f) Xác định phần thực và phần ảo của $z_1 \times z_2$
- g) Xác định môđun của $\frac{z_1}{z_2}$
- h) Chuyển $z_2$ sang dạng lượng giác
Nhấn phím HOME => chọn Complex => nhấn phím OK
1.1. Tính $z_1+z_2$
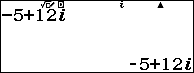
Bước 1. Nhập -5+12i
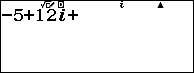
Bước 2. Nhấn phím +
Bước 3. Nhập 1+i
Bước 4. Nhấn phím EXE
Vậy $z_1+z_2=-4+13i$
Chú ý:
Nhấn phím SHIFT => nhấn phím 9 để nhập phần tử đơn vị ảo i
1.2. Tính $z_1^2$
Bước 1. Nhập -5+12i
Bước 2. Nhấn phím EXE
Bước 3. Nhấn phím
Bước 4. Nhấn phím EXE
Vậy $z_1^2=-119-120i$
1.3. Khai căn bậc hai của $z_1$
Bước 1. Nhấn phím
Bước 2. Nhấn phím CATALOG => chọn Numeric Calc => nhấn phím OK => chọn Absolute Value => nhấn phím OK
Bước 3. Nhập -5+12i
Bước 4. Nhấn phím => nhấn phím
=> nhấn phím CATALOG => chọn Complex => nhấn phím OK => chọn $\angle$ => nhấn phím OK => nhấn phím
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Bước 5. Nhấn phím CATALOG => chọn Complex => nhấn phím OK => chọn Argrumen => nhấn phím OK



=> nhập 2
Bước 7. Nhấn phím EXE
Vậy căn bậc hai của -5+12i là 2+3i và -2-3i
Chú ý:
Nếu a+bi là căn bậc hai của $z_1$ thì -a-bi cũng là căn bậc hai của $z_1$
1.4. Tính acgumen của $z_2$
Bước 1. Nhấn phím SETTINGS => chọn Calc Settings => nhấn phím OK => chọn Angle Unit => nhấn phím OK => chọn Radian => nhấn phím OK => nhấn phím AC
Chú ý:
Chỉ báo R xuất hiện chứng tỏ chúng ta đã cài đặt thành công đơn vị góc là radian
Bước 2. Nhấn phím CATALOG => chọn Complex => nhấn phím OK => chọn Argument => nhấn phím OK
Bước 3. Nhập 1+i
Bước 4. Nhấn phím EXE
Vậy acgumen của 1+i là $\frac{1}{4}\pi$
Chú ý:
Nếu bạn cài đặt đơn vị góc là độ thì acgumen của $z_2$ sẽ là $45^o$
1.5. Xác định số phức liên hợp của $z_1-z_2$
Bước 1. Nhấn phím CATALOG => chọn Complex => nhấn phím OK => chọn Conjugate => nhấn phím OK

Bước 2. Nhập -5+12i-(1+i)
Bước 3. Nhấn phím EXE
Vậy số phức liên hợp của $z_1-z_2$ là $-6-11i$
1.6. Xác định phần thực và phần ảo của $z_1 \times z_2$
Bước 1.
Bước 1.1. Nhấn phím CATALOG => chọn Complex => nhấn phím OK => chọn Real Part => nhấn phím OK
Bước 1.2. Nhập (-5+12i)(1+i)
Vậy phần thực của $z_1 \times z_2$ là -17
Bước 2.
Bước 2.1. Nhấn phím CATALOG => chọn Complex => nhấn phím OK => chọn Imaginary Part => nhấn phím OK
Bước 2.2. Nhập (-5+12i)(1+i)
Bước 2.3. Nhấn phím EXE
Vậy phần ảo của $z_1 \times z_2$ là 7
1.7. Xác định môđun của $\frac{z_1}{z_2}$
Bước 1. Nhấn phím CATALOG => chọn Numeric Calc => nhấn phím OK => chọn Absolute Value => nhấn phím OK
Bước 2. Nhập $\frac{-5+12i}{1+i}$
Bước 3. Nhấn phím EXE
Vậy môđun của $\frac{z_1}{z_2}$ là $\frac{13\sqrt{2}}{2}$
1.8. Chuyển $z_2$ sang dạng lượng giác
Bước 1. Nhấn phím SETTINGS => chọn Calc Settings => nhấn phím OK => chọn Angle Unit => nhấn phím OK => chọn Radian => nhấn phím OK => nhấn phím AC
Bước 2. Nhập 1+i
Bước 3. Nhấn phím EXE
Bước 4. Nhấn phím FORMAT => chọn Polar Coord => nhấn phím EXE
Suy ra $r=\sqrt{2}$ và $\varphi=\frac{1}{4}\pi$
Vậy dạng lượng giác của $z_2$ là $\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)$
#3. Xem video cách tính số phức bằng Casio 880 BTG
#3. Lời kết
Trên đây là cách tính số phức bằng máy tính Casio fx 880 BTG. Mình nghĩ là qua bài viết này thì chắc chắn bạn đã biết bấm máy tính để tính số phức rồi đúng không nhỉ >.<
Tính năng Complex của máy tính fx 880 BTG còn hỗ trợ chúng chuyển số phức từ dạng lượng giác sang dạng đại số, khai căn bậc ba của số phức, …
Các nội dung vừa kể trên không được nhiều người quan tâm nên mình không hướng dẫn trong phạm vi ngắn gọn của bài viết này.
Hi vọng những thông tin trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.
Đọc thêm:
- Cách cộng, trừ, nhân và chia số phức (có nhiều ví dụ)
- Cách tính lũy thừa và khai căn số phức (có nhiều ví dụ)
- Cách giải bất phương trình bằng máy tính CASIO
- Cách tìm nghiệm của phương trình chứa tham số bằng Casio
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống