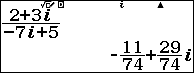Cách cộng, trừ, nhân và chia số phức (có nhiều ví dụ)

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách thực hiện bốn phép toán Số học cơ bản (cộng, trừ, nhân và chia) với số phức.

Để thuận tiện cho các bạn tiếp thu kiến thức thì trước tiên: Mình sẽ trình bày công thức tính, tiếp theo là mẹo trong khi thực hành và cuối cùng là ví dụ minh họa.

Ngoài ra mình cũng hướng dẫn thêm thủ thuật tính số phức bằng máy tính CASIO để cho các bạn thuận tiện hơn trong việc kiểm tra kết quả hoặc làm bài trắc nghiệm.

#1. Số phức là gì?

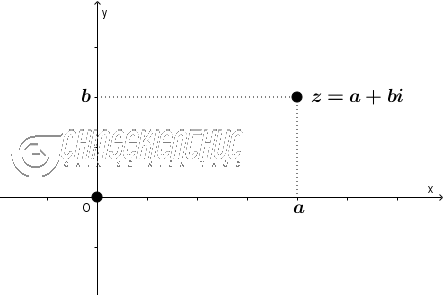
Mỗi biểu thức Toán học có dạng $a+bi$, với $a, b$ là những số thực, i là đơn vị ảo và $i^2=-1$ thì được gọi là một số phức.

Số phức $a+bi$ lần lượt có phần thực là a, phần ảo là b, còn đơn vị ảo là i

• Số phức (Complex Number) có phần thực bằng 0 được gọi là số thuần ảo.
• Số phức có phần ảo bằng 0 được gọi là số thực => mọi số thực đều là số phức.
• Số 0 = 0 + 0.i vừa là số thực, vừa là số ảo.
• Tập hợp tất cả các số phức được kí hiệu là C (kí tự đầu tiên của từ Complex).

Ví dụ 1. Các số $2+3i, 7i-5, 11, 13i$ đều là những số phức, số $11+0i$ được gọi là số thực và $0+13i$ được gọi là số thuần ảo.

#2. Cách cộng hoặc trừ hai số phức

Cho số phức $a+bi$ và $c+di$, lúc bấy giờ tổng và hiệu của hai số phức đã cho lần lượt sẽ được tính theo công thức:

• $(a+bi)+(c+di)=(a+c)+(b+d)i$
• $(a+bi)-(c+di)=(a-c)+(b-d)i$

Trong thực tiễn, mình hầu như không bao giờ áp dụng công thức trên mà mình sẽ áp dụng quy tắc cộng đa thức (xem i là biến).

Cá nhân mình cho rằng, cái gì cần nhớ thì nhớ không cần thì thôi, nhớ quá nhiều rất dễ nhầm lẫn.

Ngoài ra, mình luôn cố gắng khai thác những cái có sẵn thay vì tìm kiếm một cái mới khi chưa thật sự cần thiết.

Ví dụ 2. Thực hiện phép tính $(2+3i)+(-7i+5)$

Lời giải:

$(2+3i)+(-7i+5)=2+3i-7i+5=2+5+(3-7)i=7-4i$

Vậy => $(2+3i)+(-7i+5)=7-4i$

Cách cộng hoặc trừ hai số phức bằng máy tính CASIO fx-580VN X

Bước 1. Chọn phương thức tính toán Complex

Bước 2. Nhập phép tính $(2+3i)+(-7i+5)$

Bước 3. Nhấn phím =

Ví dụ 3. Thực hiện phép tính $(2+3i)-(-7i+5)$

Lời giải

$(2+3i)-(-7i+5)=2+3i+7i-5=2-5+(3+7)i=-3+10i$

Vậy $(2+3i)-(-7i+5)=-3+10i$

#3. Cách nhân hai số phức

Cho số phức $a+bi$ và $c+di$, lúc bấy giờ tích của hai số phức đã cho sẽ được tính theo công thức $(a+bi)(c+di)=(ac-bd)+(ad+bc)i$

Tương tự như phép tính cộng và phép tính trừ với phép tính nhân bạn cũng hãy áp dụng quy tắc nhân đa thức (xem i là biến) và nhớ thêm $i^2=-1$

Ví dụ 4. Thực hiện phép tính $(2+3i)(-7i+5)$

Lời giải:

$(2+3i)(-7i+5)=2(-7i)+2.5+3i(-7i)+3i.5=-14i+10-21i^2+15i=-14i+10+21+15i=31+i$

Vậy => $(2+3i)(-7i+5)= 31+i$

#4. Cách chia hai số phức

Trước khi tìm hiểu về cách chia hai số phức thì chúng ta cần tìm về hiểu số phức liên hợp trước.

4.1. Số phức liên hợp

Số phức liên hợp của số phức $a+bi$ là $a-bi$

Nếu đặt $z=a+bi$ thì số phức liên hợp của z thường được kí hiệu là $\bar{z}=a-bi$

Ví dụ 5. Tìm số phức liên hợp của số phức $-7i+5$

Lời giải:

Dễ thấy $-7i+5=5-7i$ suy ra số phức liên hợp của số phức $5-7i$ chính là $5+7i$

Vậy => số phức liên hợp cần tìm là $5+7i$

4.2. Công thức chia hai số phức

Cho số phức $c+di$ và $a+bi$, lúc bấy $c+di$ chia cho $a+bi$ sẽ được tính theo công thức:

$\frac{c+di}{a+bi}=\frac{ac+bd}{a^2+b^2}+\frac{ad-bc}{a^2+b^2}i$

Ví dụ 6. Thực hiện phép tính $\frac{2+3i}{-7i+5}$

Lời giải:

$\frac{2+3i}{-7i+5}=\frac{(2+3i)(7i+5)}{(-7i+5)(7i+5)}=\frac{-11+29i}{74}=-\frac{11}{74}+\frac{29}{74}i$

#5. Lời kết

Đến đây thì bạn đã có thể tìm được số phức liên hợp và thực hiện được bốn phép tính số học cơ bản (cộng, trừ, nhân và chia) với hai số phức rồi phải không nào?!

Trường hợp cần thực hiện với ba, bốn, năm, …, số phức thì thao tác hoàn toàn tương tự, vì phép cộng và phép nhân các số phức cũng có các tính chất như phép cộng và phép nhân các số thực vậy.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tất cả các bạn và hẹn gặp lại trong những bài viết tiếp theo nhé 🙂

Đọc thêm:

• 2 cách tìm giá trị lớn nhất, nhỏ nhất của hàm số
• Cách viết phương trình đường thẳng trên mặt phẳng
• Cách tìm cực trị của hàm số đa thức (bậc 2 và bậc 3)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn