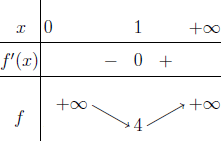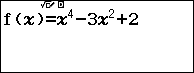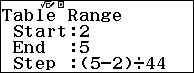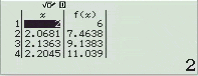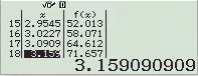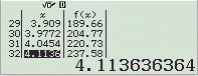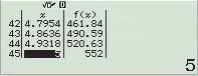Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số trên một khoảng hoặc trên một đoạn cho trước.
Để thuận tiện cho việc hướng dẫn thì mình sẽ chia bài viết thành hai trường hợp: Trường hợp 1: Trên khoảng và Trường hợp 2: Trên đoạn
Ứng với mỗi trường hợp sẽ có những phương pháp giải khác nhau, riêng Trường hợp 2 mình sẽ giới thiệu thêm phương pháp tính nhanh bằng cách sử dụng máy tính CASIO fx-580VN X.
Mục Lục Nội Dung
Trường hợp #1: Trên khoảng
CÁC BƯỚC:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) trên khoảng (a; b) cho trước.
Bước 1. Tìm $f’(x)$
Bước 2. Tìm những giá trị làm cho $f’(x)=0$ hoặc $f’(x)$ không xác định.
Chú ý: Loại ra những giá trị không thuộc khoảng (a; b) cho trước.
Bước 3. Lập bảng biến thiên.
Bước 4. Kết luận.
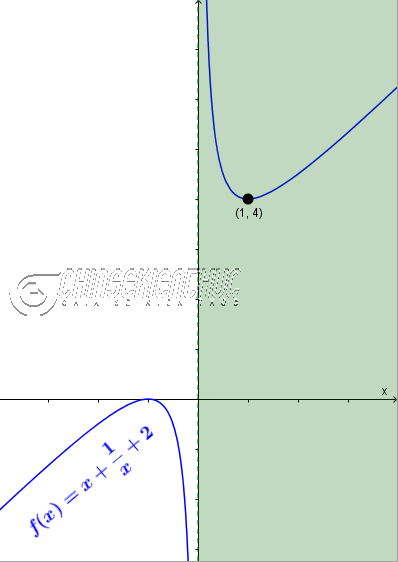
Ví dụ 1. Tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số $f(x)=x+\frac{1}{x}+2$ trên khoảng $(0; +\infty)$
Lời giải:
Trên khoảng $(0; +\infty)$ chúng ta có …
$f’(x)=1-\frac{1}{x^2}$
$f’(x)=0 \Leftrightarrow 1-\frac{1}{x^2}=0 \Leftrightarrow \frac{x^2-1}{x^2} \Leftrightarrow x^2-1=0 \Leftrightarrow x=1$
Bảng biến thiên:
Quan sát bảng biến thiên chúng ta thấy trên khoảng $(0; +\infty)$ hàm số $f(x)=x+\frac{1}{x}+2$ có giá trị nhỏ nhất là 4 đạt được khi x bằng 1
Vậy $\min_{(0; +\infty)} f(x)=4$ khi $x=1$ và $\max_{(0; +\infty)} f(x)$ không tồn tại.
Chú ý:
- Vì chúng ta đang xét trên khoảng $(0; +\infty)$ nên chúng ta mới có $\frac{x^2-1}{x^2} \Leftrightarrow x^2-1=0 \Leftrightarrow x=1$
- Nếu đề bài không yêu cầu tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đâu thì mặc định chúng ta sẽ tìm trên tập xác định.
Trường hợp #2: Trên đoạn
Khi được yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn nào đó thì bạn có thể áp dụng một trong hai phương pháp bên dưới.
- Cách #1. Dựa vào kiến thức Toán học, tất nhiên đây là phương pháp chính thống, áp dụng được cho cả hai hình thức là trắc nghiệm và tự luận.
- Cách #2. Dựa vào tính năng Table của mình tính CASIO FX-580VN X, phương pháp này tuy khá nhanh nhưng ít nhiều gì cũng có sai sót nhất định và không thể áp dụng với dạng tự luận.
Cách #1. Dựa vào kiến thức Toán học
CÁC BƯỚC:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b] cho trước.
Bước 1. Tìm các điểm $x_1, x_2, x_3, \cdots, x_n$ thuộc khoảng $(a; b)$ mà tại đó $f’(x)$ bằng 0 hoặc $f’(x)$ không xác định.
Bước 2. Tính $f(a), f(x_1), f(x_2), f(x_3), \cdots, f(x_n), f(b)$
Bước 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất trong các giá trị vừa tính được.
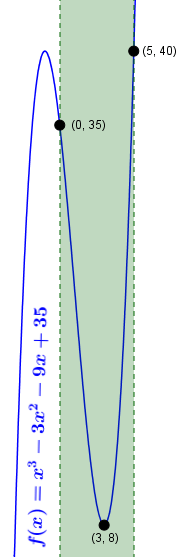
Ví dụ 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x)=x^3-3x^2-9x+35$ trên đoạn $[0; 5]$
Lời giải:
Trên đoạn [0; 5] chúng ta có …
$f’(x)=3(x^2-2x-3)$
$f’(x)=0 \Leftrightarrow 3(x^2-2x-3)=0 \Leftrightarrow 3(x+1)(x-3)=0 \Leftrightarrow x=3$
$f(0)=35$
$f(3)=8$
$f(5)=40$
Vậy $\min_{[0; 5]} f(x)=8$ khi $x=3$ và $\max_{[0; 5]} f(x)=40$ khi $x=5$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Cách #2. Sử dụng máy tính CASIO để tìm GTLN, GTNN của hàm số
Ví dụ 3. Tìm giá trị lớn nhất và nhỏ nhất của hàm số $f(x)=x^4-3x^2+2$ trên đoạn $[2; 5]$
Các bước thực hiện:
Bước 1. Lần lượt nhấn các phím 
để tắt hàm g(x)
Bước 2. Chọn phương thức Table
Bước 3. Nhập hàm số $f(x)=x^4-3x^2+2$
Bước 4. Nhấn phím = => nhập $Start=2, End=5, Step=(5-2) \div 44$
Bước 5. Nhấn phím = => nhấn tiếp phím =
Quan sát bảng giá trị tìm được chúng ta nhận thấy giá trị lớn nhất của hàm số là 552 khi x = 5 và giá trị nhỏ nhất là 6 khi x = 2
Vậy $\max_{[2; 5]} f(x)=552$ khi $x=5$ và $\min_{[2; 5]} f(x)=6$ khi $x=2$
Chú ý:
Máy tính CASIO fx-570ES Plus và CASIO fx-570 VN Plus vẫn có thể thực hiện được thủ thuật này nhưng quá trình cài đặt tắt hàm g(x) sẽ khác và $Step=(5-2) \div 29$.
Có thể bạn đang tìm?
Cách tìm MAX, MIN của hàm số bằng máy tính CASIO (580 VNX và 880 BTG)
Lời kết
Tùy thuộc vào yêu cầu của bài toán là tìm giá trị lớn nhất (GTLN), hay giá trị nhỏ nhất (GTNN) trên khoảng hay trên đoạn mà chúng ta sẽ áp dụng các phương pháp cho phù hợp nhất.
Phương pháp sử dụng máy tính CASIO tuy nhanh nhưng nó cũng có sai sót nhất định, nhất là khi khoảng cách giữa hai đầu mút quá lớn, chẳng hạn như [1; 45]
Ngoài ra, khi tìm các nghiệm của phương trình $f’(x)=0$ hoặc các giá trị không xác định của $f’(x)$ đừng quên loại bỏ những nghiệm, giá trị không thuộc khoảng hoặc đoạn mà đề bài yêu cầu
Hi vọng những kiến thức trong bài viết này hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
