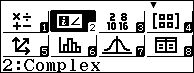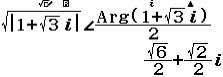Cách tính lũy thừa và khai căn số phức (có nhiều ví dụ)

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tính lũy thừa và khai căn số phức ha.

Mình sẽ hướng dẫn các bạn thực hiện với dạng đại số và cả dạng lượng giác để các bạn có thể so sánh ưu nhược điểm của từng cách.

Ngoài ra thì mình cũng hướng dẫn thêm cho bạn cách tính lũy thừa và khai căn số phức bằng máy tính CASIO nhằm phục vụ cho kì thi Trung học Phổ thông Quốc gia.

I. Phép tính lũy thừa

Phép tính lũy thừa có thể thực hiện dễ dàng ở dạng đại số và dạng lượng giác.

Tuy nhiên, nếu số mũ lớn thì bạn nên ưu tiên thực hiện dưới dạng lượng giác hơn.

Trường hợp #1. Số phức được cho dưới dạng Đại số

Cho số phức $z=a+bi$, lúc bấy giờ $z^n=(a+bi)^n$

Công thức chứng minh cho trường hợp $n=2, n=3$ và $n=4$

• $(a+bi)^2=(a^2-b^2)+(2ab)i$
• $(a+bi)^3=(a^3-3ab^2)+(3a^2b-b^3)i$
• $(a+bi)^4=(a^4+b^4-6a^2b^2)+(4a^3b-4ab^3)i$

Trong thực hành, khi cần tính lũy thừa của số phức ở dạng đại số bạn hãy xem số phức là một nhị thức bậc nhất với biến là i rồi:

Bước 1. Áp dụng các hằng đẳng thức đắng nhớ hoặc nhị thức Newton hoặc định nghĩa lũy thừa để khai triển.

Bước 2. Thu gọn biểu thức tương tự như thu gọn đa thức, nhưng nhớ thu gọn luôn $i^n$:

• Nếu $n=4k$ thì $i^n=1$
• Nếu $n=4k+1$ thì $i^n=i$
• Nếu $n=4k+2$ thì $i^n=-1$
• Nếu $n=4k+3$ thì $i^n=-i$

Ví dụ. Tính $i^{2019}, i^{2020}, i^{2021}, i^{2022}$

Lời giải:

$i^{2019}=i^{4.504+3}=-i$

$i^{2020}= i^{4.505}=1$

$i^{2021}= i^{4.505+1}=i$

$i^{2022}=i^{4.505+2}=-1$

Trường hợp #2. Số phức được cho dưới dạng lượng giác

Cho số phức $z=r(\cos \varphi+i\sin \varphi)$, lúc bấy giờ $z^n=r^n(\cos n\varphi+i\sin n\varphi)$

II. Phép tính khai căn

Việc khai căn số phức ở dạng đại số khá phức tạp (trừ khai căn bậc hai) nên trong phạm vi ngắn gọn của bài viết này mình chỉ trình bày cách khai căn số phức dưới dạng lượng giác thôi nha các bạn.

Cho số phức $z=r(\cos \varphi+i\sin \varphi)$ lúc bấy giờ $\sqrt[n]{z}=\sqrt[n]{r}(\cos \frac{\varphi+k2\pi}{n}+i\sin \frac{\varphi+k2\pi}{n})$ với $k=0, 1, 2, \cdots, n-1$

III. Bài tập ví dụ minh họa

Ví dụ 1. Cho số phức $z=2+3i$ tính $z^2$

Lời giải:

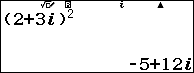
$(2+3i)^2=2^2+2.2.3i+(3i)^2=4+12i-9=-5+12i$

Vậy $z^2=-5+12i$

Ví dụ 2. Cho số phức $z=(\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i)$ tính $z^5$

Lời giải:

Dễ thấy, dạng lượng giác của số phức $\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i$ là $2(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12})$

Xem thêm:
Cách chuyển số phức từ dạng đại số sang dạng lượng giác và ngược lại

Suy ra $z^5$ sẽ bằng $2^5(\cos\frac{5\pi}{12}+i\sin\frac{5\pi}{12})=32(\cos\frac{5\pi}{12}+i\sin\frac{5\pi}{12})$ hay $(8\sqrt{6}-8\sqrt{2})+(8\sqrt{6}+8\sqrt{2})i$

Vậy $z^5=(8\sqrt{6}-8\sqrt{2})+(8\sqrt{6}+8\sqrt{2})i$

Ví dụ 3. Cho số phức z bằng $1+\sqrt{3}i$ tính $\sqrt{z}$

Quá trình tìm tòi lời giải:

Đầu tiên chúng ta sẽ chuyển số phức $z=1+\sqrt{3}i$ sang dạng lượng giác.

Tiếp theo bạn áp dụng công thức $\sqrt[n]{z}=\sqrt[n]{r}(\cos \frac{\varphi+k2\pi}{n}+i\sin \frac{\varphi+k2\pi}{n})$, với $k=0, 1, 2, \cdots, n-1$ là xong.

Lời giải:

Số phức $z$ có dạng lượng giác là $r(\cos \varphi+i\sin \varphi)$

$\sqrt{(1)^2+(\sqrt{3})^2}=2$

Lúc bấy giờ, số phức $z=2\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)$

Dễ thấy $r=2$ và $\varphi$ là nghiệm của hệ hai phương trình hai ẩn $\left\{\begin{array}{ll}\cos \varphi&=\frac{1}{2} \\\sin \varphi&=\frac{\sqrt{3}}{2}\end{array}\right.$

Dễ thấy $\varphi=\frac{\pi}{3}$ thỏa mãn hệ phương trình

Vậy dạng lượng giác của số phức $1+\sqrt{3}i$  là $2(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3})$

$\sqrt{z}=\sqrt{2}(\cos \frac{\frac{\pi}{3}+k2\pi}{2}+i\sin \frac{\frac{\pi}{3}+k2\pi}{2})$ với $k=0, 1$

Cụ thể $\sqrt{z}$ sẽ bằng $\sqrt{2}(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6})$ và $\sqrt{2}(\cos \frac{7\pi}{6}+i\sin \frac{7\pi}{6})$

Vậy hai căn bậc hai cần tìm là $\sqrt{2}(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6})$ và $\sqrt{2}(\cos \frac{7\pi}{6}+i\sin \frac{7\pi}{6})$ hay $\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2}i$ và $-\frac{\sqrt{6}}{2}-\frac{\sqrt{2}}{2}i$

IV. Tính nhanh lũy thừa, căn bậc hai bằng máy tính CASIO

Máy tính CASIO fx-580VN X cho phép bạn tính được lũy thừa mũ n, nhưng chỉ cho phép khai căn bậc hai.

#1. Tính lũy thừa bằng máy tính Casio

Giả sử cần tính $z^2$ biết số phức $z=2+3i$

Bước 1. Chọn phương thức tính toán Complex

Bước 2. Nhập biểu thức => nhấn phím =

#2. Tính căn bậc hai bằng máy tính Casio

Giả sử cần tính $\sqrt{z}$ biết $z=1+\sqrt{3}i$

Bước 1. Chọn phương thức tính toán Complex

Bước 2. Nhập biểu thức $\sqrt{|1+\sqrt{3}i|} \angle \frac{Arg(1+\sqrt{3}i)}{2}$

Bước 3. Nhấn phím =

Vậy hai căn bậc hai cần tìm là $\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2}i$ và $–(\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2}i)$

V. Lời kết

Okay, như vậy là mình đã hướng dẫn rất chi tiết cho bạn cách tính lũy thừa và khai căn số phức rồi nhé.

Nếu phép tính lũy thừa với mũ hai, mũ ba thì bạn có thể thực hiện trực tiếp với dạng đại số, nhưng nếu mũ cao hơn thì nên thực hiện với dạng lượng giác

Trường hợp khai căn cũng vậy, nếu là căn bậc hai thì bạn có thể thực hiện với dạng đại số, nhưng nếu là căn bậc ba, căn bậc bốn, … thì nhất thiết phải thực hiện với dạng lượng giác

Hi vọng kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 2 cách giải bất phương trình bậc hai một ẩn, rất dễ
• 3 cách tính diện tích tam giác tạo bởi ba điểm cực trị
• Cách tìm cực trị của hàm số đa thức (bậc 2 và bậc 3)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn