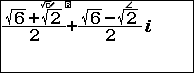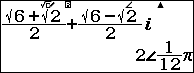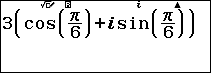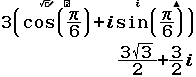Chuyển số phức từ dạng đại số sang lượng giác và ngược lại

Không giống như số thực (chỉ có một dạng duy nhất), số phức ngoài dạng đại số ra thì còn có dạng lượng giác và dạng số mũ nữa.

Thông thường khi mới làm quen với số phức thì chúng ta sẽ tiếp cận với dạng đại số vì dạng này có tính sư phạm hơn (dễ tiếp cận, dễ dạy và dễ học).

Tuy nhiên, sau một thời gian làm quen với số phức thì chúng ta nên tìm hiểu dạng lượng giác, vì dạng này sẽ thuận tiện hơn khi thực hiện các phép tính nhân, chia, lũy thừa và khai căn..

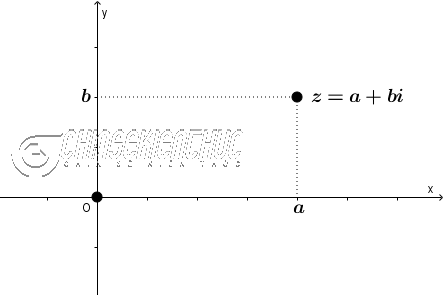
#1. Dạng đại số của số phức

Số phức z có dạng đại số là $a+bi$, với a, b là những số thực và $i^2=-1$

Ví dụ 1. Các số phức $\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i, \frac{3\sqrt{3}}{2}+\frac{3}{2}i, -5, 7i$ đều là những số phức được cho dưới dạng đại số.

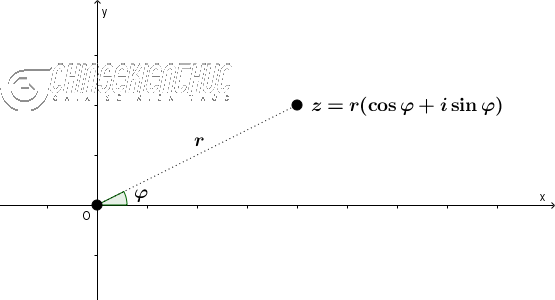
#2. Dạng lượng giác của số phức

Số phức z có dạng lượng giác là $r(\cos \varphi+i\sin \varphi)$

Ví dụ 2. Các số phức $2(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12}), 3(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}), 5(\cos\pi+i\sin\pi), 7(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2})$ đều là những số phức được cho dưới dạng lượng giác.

#3. Ưu điểm của số phức dạng lượng giác

Số phức dưới dạng lượng giác có nhiều ưu điểm, dưới đây là một số ưu điểm tiêu biểu nhất:

• Để tính nhanh phép nhân và phép chia hai số phức.
• Để tính lũy thừa và khai căn số phức.

Trường hợp phép nhân và phép chia nếu không chuyển sang dạng lượng giác thì vẫn tính được nhưng khá là chậm.

Trường hợp phép lũy thừa và khai căn nếu không chuyển sang dạng lượng giác thì sẽ tốn khá nhiều thời gian và công sức. Có thể sẽ bế tắc khi lũy thừa với số mũ quá lớn hoặc khai căn bậc ba.

#4. Cách chuyển số phức từ dạng đại số sang dạng lượng giác

Mọi số phức đều có thể chuyển từ dạng đại số sang dạng lượng giác, vấn đề là r và $\varphi$ là “đẹp” hay “xấu” mà thôi.

Ta có số phức z được biểu diễn dưới dạng đại số là:

$a+bi$ hay $\sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}+\frac{b}{\sqrt{a^2+b^2}}i\right)$

Mặt khác, ta lại có số phức z được biểu diễn dưới dạng lượng giác là $r(\cos \varphi+i\sin \varphi)$.

Suy ra $r=\sqrt{a^2+b^2}$, $\varphi$ là nghiệm của hệ hai phương trình một ẩn $\left\{\begin{array}{ll}\cos \varphi&=\frac{a}{\sqrt{a^2+b^2}} \\\sin \varphi&=\frac{b}{\sqrt{a^2+b^2}}\end{array}\right.$

Tóm lại, bạn chỉ cần tìm được r và $\varphi$ là tìm được dạng lượng giác của số phức.

Ví dụ 3. Chuyển số phức $\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i$ sang dạng lượng giác

Lời giải:

Đặt $z=\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i$

Số phức $z$ có dạng lượng giác là $r(\cos \varphi+i\sin \varphi)$

$\sqrt{\left(\frac{\sqrt{6}+\sqrt{2}}{2}\right)^2+\left(\frac{\sqrt{6}-\sqrt{2}}{2}\right)^2}=2$

Lúc bấy giờ số phức $z=2\left(\frac{\sqrt{6}+\sqrt{2}}{4}+\frac{\sqrt{6}-\sqrt{2}}{4}i\right)$

Dễ thấy $r=2$ và $\varphi$ là nghiệm của hệ hai phương trình hai ẩn $\left\{\begin{array}{ll}\cos \varphi&=\frac{\sqrt{6}+\sqrt{2}}{4} \\\sin \varphi&=\frac{\sqrt{6}-\sqrt{2}}{4}\end{array}\right.$

Dễ thấy $\varphi=\frac{\pi}{12}$ thỏa mãn hệ phương trình (thật ra mình bấm máy tính ra đó các bạn, không có thấy được đâu :D)

Vậy dạng lượng giác của số phức $\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i$ là $2(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12})$

Chuyển số phức từ dạng đại số sang dạng lượng giác bằng máy tính CASIO fx-580VN X

Bước 1. Bạn lần lượt nhấn các phím  để cài đặt đơn vị góc là radian

Bước 2. Lần lượt nhấn các phím  để cài đặt dạng hiển thị của số phức sau khi nhấn phím = là dạng lượng giác.

Bước 3. Chọn phương thức tính toán Complex

Bước 4. Nhập dạng đại số của số phức vào máy tính.

Bước 5. Nhấn phím =

Vậy dạng lượng giác của số phức $\frac{\sqrt{6}+\sqrt{2}}{2}+\frac{\sqrt{6}-\sqrt{2}}{2}i$ là $2(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12})$

#5. Cách chuyển số phức từ dạng lượng giác sang dạng đại số

Mọi số phức đều có thể chuyển từ dạng lượng giác sang dạng đại số một cách dễ dàng nếu so với chiều ngược lại

Ví dụ 4. Chuyển số phức $3(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})$ sang dạng đại số.

Lời giải:

$\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}$ và $\sin\frac{\pi}{6}=\frac{1}{2}$

Vậy dạng đại số của số phức $3(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})$ là $\frac{3\sqrt{3}}{2}+\frac{3}{2}i$

Chuyển số phức từ dạng lượng giác sang dạng đại số bằng máy tính CASIO fx-580VN X

Bước 1. Bạn lần lượt nhấn các phím để cài đặt đơn vị góc là radian.

Bước 2. Lần lượt nhấn các phím  để cài đặt dạng hiển thị của số phức sau khi nhấn phím = là dạng đại số.

Bước 3. Chọn phương thức tính toán Complex

Bước 4. Nhập dạng đại số của số phức vào máy tính

Bước 5. Nhấn phím =

Vậy dạng đại số của số phức $3(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})$ là $\frac{3\sqrt{3}}{2}+\frac{3}{2}i$

#6. Lời kết

Khi được yêu cầu chuyển một số phức từ dạng đại số sang dạng lượng giác và ngược lại nếu:

• Thi tự luận thì bạn phải sử dụng phương pháp Toán học (nên sử dụng thêm phương pháp máy tính để tìm nhanh r và $\varphi$) mới được hưởng trọn điểm.
• Trắc nghiệm thì bạn chỉ cần sử dụng phương pháp máy tính là xong, cho nó nhanh.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn