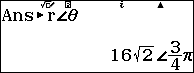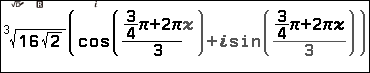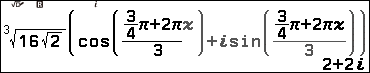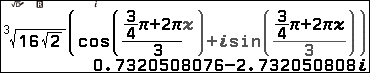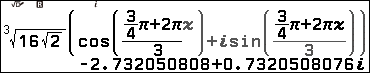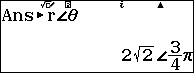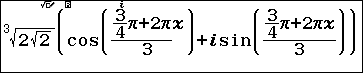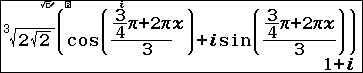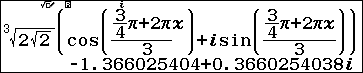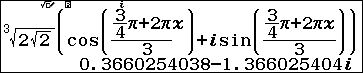Bấm máy tính khai căn bậc 3 số phức (Casio 580 & 880)

Như các bạn đã biết thì máy tính CASIO cho phép chúng ta thực hiện rất nhiều phép tính với các số phức như phép tính cộng, trừ, nhân, chia, lũy thừa, …

Phép khai căn bậc hai mặc dù chưa được hỗ trợ nhưng bằng cách kết hợp các tính năng sẵn có chúng ta vẫn thực hiện được một cách dễ dàng.

Tương tự như phép khai căn bậc hai thì hôm nay, mình sẽ hướng dẫn cho các bạn cách kết hợp các tính năng có sẵn trên máy tính CASIO và kiến thức Toán học để khai căn bậc ba của một số phức bất kỳ.

#1. Tìm hiểu về dạng lượng giác của số phức

Số phức z được viết dưới dạng đại số là a+bi, với a, b là những số thực và $i^2=-1$

Số phức z được viết dưới dạng lượng giác là $r(\cos \varphi + i \sin \varphi)$ với $r=\sqrt{a^2+b^2}$ và $\left\{\begin{array}{}\cos \varphi&=\frac{a}{\sqrt{a^2+b^2}} \\ \sin \varphi&=\frac{b}{\sqrt{a^2+b^2}}\end{array}\right.$

#2. Công thức khai căn bậc 3 số phức

Nếu số phức đã được viết dưới dạng lượng giác thì các bạn hãy áp dụng công thức bên dưới để tiến hành khai căn bậc 3.

Cho số phức $z=r(\cos \varphi+i \sin \varphi)$, lúc này công thức khai căn bậc 3 sẽ là:

$\sqrt[3]{z}=\sqrt[3]{r}\left(\cos \frac{\varphi+k 2 \pi}{3}+i \sin \frac{\varphi+k 2 \pi}{3}\right)$ với k=0, 1, 2

#3. Các bước khai căn bậc 3 số phức

Bước 1. Chuyển số phức sang dạng lượng giác

Xem thêm: Chuyển số phức từ dạng đại số sang dạng lượng giác

Bước 2. Áp dụng công thức khai căn bậc ba.

#4. Cách khai căn bậc ba số phức trên Casio 880 BTG

Ví dụ. Khai căn bậc ba của số phức z=-16+16i

Bước 1. Chuyển số phức sang dạng lượng giác như sau.

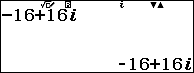
Suy ra dạng lượng giác của số phức đã cho là $16\sqrt{2}\left(\cos \frac{3}{4}\pi+i\sin \frac{3}{4}\pi\right)$

Bước 2. Áp dụng công thức khai căn bậc ba.

Áp dụng công thức khai căn bậc ba vào ví dụ trên chúng ta thu được:

$\sqrt[3]{16\sqrt{2}}\left(\cos \frac{\frac{3}{4}\pi+k 2 \pi}{3}+i \sin \frac{\frac{3}{4}\pi+k 2 \pi}{3}\right)$ với k=0, 1, 2

Nếu muốn viết cụ thể hơn thì bạn có thể thực hiện thêm theo các thao tác được liệt kê bên dưới

2.1. Nhập $\sqrt[3]{16\sqrt{2}}\left(\cos \frac{\frac{3}{4}\pi+ 2 \pi x}{3}+i \sin \frac{\frac{3}{4}\pi+ 2 \pi x}{3}\right)$

Chú ý.
Vì máy tính CASIO không có biến nhớ k nên chúng ta sẽ thay bằng biến nhớ x

2.2. Nhấn phím VARAIBLE => chọn biến nhớ x => nhập 0 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

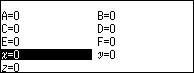
2.3. Nhấn phím VARAIBLE => chọn biến nhớ x => nhập 1 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE

2.4. Nhấn phím VARAIBLE => chọn biến nhớ x => nhập 2 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE

Xem video hướng dẫn thực hiện trên Casio 880 BTG

#5. Cách khai căn bậc 3 trên máy fx 580 VNX

Ví dụ. Khai căn bậc ba của số phức z=-2+2i

Bước 1. Chuyển số phức sang dạng lượng giác

Suy ra dạng lượng giác của số phức đã cho là $2\sqrt{2}\left(\cos \frac{3}{4}\pi+i\sin \frac{3}{4}\pi\right)$

Bước 2. Áp dụng công thức khai căn bậc ba.

Áp dụng công thức khai căn bậc ba chúng ta thu được:

$\sqrt[3]{2\sqrt{2}}\left(\cos \frac{\frac{3}{4}\pi+k 2 \pi}{3}+i \sin \frac{\frac{3}{4}\pi+k 2 \pi}{3}\right)$ với k=0, 1, 2

Nếu muốn viết cụ thể hơn thì bạn có thể thực hiện thêm theo các thao tác được liệt kê bên dưới

2.1. Nhập $\sqrt[3]{2\sqrt{2}}\left(\cos \frac{\frac{3}{4}\pi+ 2 \pi x}{3}+i \sin \frac{\frac{3}{4}\pi+ 2 \pi x}{3}\right)$

Chú ý.
Vì máy tính CASIO không có biến nhớ k nên chúng ta sẽ thay bằng biến nhớ x

2.2. Nhấn phím CALC => nhập 0 => nhấn phím = => nhấn phím =

2.3. Nhấn phím CALC => nhập 1 => nhấn phím = => nhấn phím =

2.4. Nhấn phím CALC => nhập 2 => nhấn phím = => nhấn phím =

Xem video hướng dẫn thực hiện trên Casio 580 VNX

#6. Lời kết

Bài toán khai căn bậc ba của số phức thường chỉ gặp trong chương trình Đại học, cụ thể hơn là trong môn Toán học cao cấp.

Lúc này, việc áp dụng thủ thuật trên sẽ giúp bạn khai căn bậc ba của số phức một cách chính xác và nhanh chóng hơn.

Trường hợp cần khai căn bậc bốn, bậc năm, bậc sáu,… thì bạn cũng thực hiện tương tự nhưng áp dụng công thức khai căn cho phù hợp nhé.

Cho số phức $z=r(\cos \varphi+i \sin \varphi)$ lúc này $\sqrt[n]{z}=\sqrt[n]{r}\left(\cos \frac{\varphi+k 2 \pi}{n}+i \sin \frac{\varphi+k 2 \pi}{n}\right)$ với $k=0,1,2, \cdots, n-1$

Hi vọng bài viết này sẽ hữu ích vơi bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

Đọc thêm:

• Cách khai căn bậc n của số phức và bài tập ví dụ
• Tổng hợp 12 công thức số phức thường gặp nhất
• Cách cộng, trừ, nhân và chia số phức (có nhiều ví dụ)
• Cách tính lũy thừa và khai căn số phức (có nhiều ví dụ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn