Tổng hợp 12 công thức số phức thường gặp nhất

Hôm nay, mình sẽ liệt kê cho các bạn toàn bộ các công thức số phức thường gặp trong chương trình Toán học Trung học Phổ thông.

Mình sẽ bắt đầu với định nghĩa số phức, hai số phức bằng nhau, phép cộng hai số phức, … và kết thức bằng khai căn của số phức

#1. Số phức là số như thế nào?

Một biểu thức dạng $a+b i$ với $a$ và $b$ là những số thực và số $i$ thoả mãn $i^2=-1$ được gọi là một số phức

Ký hiệu của số phức là $z$ và viết $z=a+b i$

Lúc này $i$ được gọi là đơn vị ảo, $a$ được gọi là phần thực và $b$ được gọi là phần ảo.

#2. Hai số phức bằng nhau khi nào?

Cho số phức $z=a+b i$ với $a, b \in \mathbb{R}$ và số phức $z^{\prime}=a^{\prime}+b^{\prime} i$ với $a^{\prime}, b^{\prime} \in \mathbb{R}$ gọi là bằng nhau khi $a=a^{\prime}$ và $b=b^{\prime}$

Lúc này, chúng ta viết $z=z^{\prime}$

#3. Thực hiện phép cộng hai số phức

+) Định nghĩa

Tổng của hai số phức $z=a+b i, z^{\prime}=a^{\prime}+b^{\prime} i$ với $a, b, a^{\prime}, b^{\prime} \in \mathbb{R}$ là số phức $z+z^{\prime}=a+a^{\prime}+\left(b+b^{\prime}\right) i$

Để cộng hai số phức chúng ta cộng các phần thực với nhau và cộng các phần ảo với nhau

Ví dụ 1. Cho số phức $z=2+3i$ và số phức $z’=5+7i$. Tính $z+z’$

Lời giải:

$z+z’$ $=(2+3i)+(5+7i)$ $=(2+5)+(3+7)i$ $=7+10i$

+) Tính chất

Tương tự với phép cộng các số thực, phép cộng các số phức cũng có các tính chất kết hợp, giao hoán và cộng với $0$:

• Tính chất kết hợp của số phức: $\left(z+z^{\prime}\right)+z^{\prime \prime}=z+\left(z^{\prime}+z^{\prime \prime}\right)$ với mọi $z, z^{\prime}, z^{\prime \prime} \in \mathbb{C}$
• Tính chất giao hoán của số phức: $z+z^{\prime}=z^{\prime}+z$ với mọi $z, z^{\prime} \in \mathbb{C}$
• Cộng với số không $z+0=0+z=z$ với mọi $z \in \mathbb{C}$

#4. Thực hiện phép trừ hai số phức

Nếu $z=a+b i, z^{\prime}=a^{\prime}+b^{\prime} i$ với

$a, b, a^{\prime}, b^{\prime} \in \mathbb{R}$ thì $z-z^{\prime}=a-a^{\prime}+\left(b-b^{\prime}\right) i$

Ví dụ 2. Cho số phức $z=2+3i$ và số phức $z’=5+7i$. Tính $z-z’$

Lời giải:

$z-z’$ $=(2+3i)-(5+7i)$ $=(2-5)+(3-7)i$ $=-3-4i$

#5. Thực hiện phép nhân hai số phức

+) Định nghĩa

Tích của số phức $z=a+b i$ và số phức $z^{\prime}=a^{\prime}+b^{\prime} i$ với $a, b, a^{\prime}, b^{\prime} \in \mathbb{R}$ là số phức $z z^{\prime}=a a^{\prime}-b b^{\prime}+\left(a b^{\prime}+a^{\prime} b\right) i$

Trong thực hành, để nhân số phức $z=a+b i$ và số phức $z^{\prime}=a^{\prime}+b^{\prime} i$ thì chúng ta sẽ thực hiện phép nhân biểu thức $a+b i$ với biểu thức $a^{\prime}+b^{\prime} i$ rồi thay $i^2=-1$

Ví dụ 3. Cho số phức $z=2+3i$ và số phức $z’=5+7i$. Tính $zz’$

Lời giải:

$z.z’$ $=(2+3i).(5+7i)$ $=(2.5-3.7)+(2.7+5.3)i$ $=-11+29i$

+) Tính chất

Dễ thấy, phép nhân các số phức cũng có các tính chất tương tự phép nhân các số thực:

• Tính chất giao hoán $z z^{\prime}=z^{\prime} z$ với mọi $z, z^{\prime} \in \mathbb{C}$
• Tính chất kết hợp $\left(z z^{\prime}\right) z^{\prime \prime}=z\left(z^{\prime} z^{\prime \prime}\right)$ với mọi $z, z^{\prime}, z^{\prime \prime} \in \mathbb{C}$
• Nhân với số một $1.z=z .1=z$ với mọi $z \in \mathbb{C}$
• Tính chất phân phối của phép nhân đối với phép cộng $z\left(z^{\prime}+z^{\prime \prime}\right)=z z^{\prime}+z z^{\prime \prime}$ với mọi $z, z^{\prime}, z^{\prime \prime} \in \mathbb{C}$

#6. Số phức liên hợp

Số phức liên hợp của $z=a+b i$ với $a, b \in \mathbb{R}$ là $a-b i$ và được ký hiệu là $\bar{z}$

Chúng ta có công thức $\bar{z}=\overline{a+b i}=a-b i$

Ví dụ 4. Cho số phức $z=2+3i$. Tính $\bar{z}$

Lời giải:

$\bar{z}=2-3i$

#7. Mô đun của số phức

Mô đun của số phức $z=a+b i$ với $a, b \in \mathbb{R}$ là số thực không âm $\sqrt{a^2+b^2}$ và được ký hiệu là $|z|$

Chúng ta có công thức nếu $z=a+b i$ với $a, b \in \mathbb{R}$ thì $|z|=\sqrt{z \bar{z}}=\sqrt{a^2+b^2}$

Ví dụ 5. Cho số phức $z=2+3i$. Tính $|z|$

Lời giải:

$|z|=\sqrt{2^2+3^2}=\sqrt{15}$

#8. Phép chia hai số phức

Trước khi tìm hiểu cách chia hai số phức chúng ta cần tìm hiểu về số nghịch đảo.

Số phức nghịch đảo của số phức $z$ khác $0$ là số $z^{-1}=\frac{1}{|z|^2} \bar{z}$

Lúc này thương $\frac{z^{\prime}}{z}$ của phép chia số phức $z^{\prime}$ cho số phức $z$ khác $0$ là tích của $z^{\prime}$ với số phức nghịch đảo của $z$, tức là $\frac{z^{\prime}}{z}=z^{\prime} z^{-1}$

Chúng ta có công thức nếu $z \neq 0$ thì $\frac{z^{\prime}}{z}=\frac{z^{\prime} \bar{z}}{|z|^2}$

Ví dụ 6. Cho số phức $z_1=2+3i$ và số phức $z_2=5+7i$. Tính $\frac{z_1}{z_2}$

Lời giải:

$\frac{z_1}{z_2}=\frac{2+3i}{5+7i}=\frac{(2+3i)(5-7i)}{(5+7i)(5-7i)}=\frac{31}{74}+\frac{1}{74}i$

#9. Căn bậc hai của số phức

Cho số phức $w$, mỗi số phức $z$ thoả mãn $z^2=w$ được gọi là một căn bậc hai của $w$

Nói cách khác mỗi căn bậc hai của $w$ là một nghiệm của phương trình $z^2-w=0$ với ẩn $z$

Chúng ta có thể tìm căn bậc hai của số phức $w$ bằng cách thực hiện tuần tự theo các chỉ dẫn bên dưới:

Cho số phức $w=a+b i$ với $a, b \in \mathbb{R}, b \neq 0$

Lúc này số phức $z=x+y i$ với $x, y \in \mathbb{R}$ là căn bậc hai của $w$ <=> $z^2=w$ tức là $(x+y i)^2=a+b i$

Vì $(x+y i)^2=x^2-y^2+2 x y i$ nên $z^2=w$ <=> $\left\{\begin{array}{l}x^2-y^2=a \\ 2 x y=b \end{array}\right.$

Tóm lại, để tìm các căn bậc hai của $w=a+b i$ thì chúng ta cần giải hệ phương trình mà mình vừa trình bày bên trên.

Mỗi cặp số thực $(x ; y)$ là nghiệm đúng của hệ phương trình cho ta một căn bậc hai $x+y i$ của số phức $a+b i$

#10. Ác-gu-men của số phức

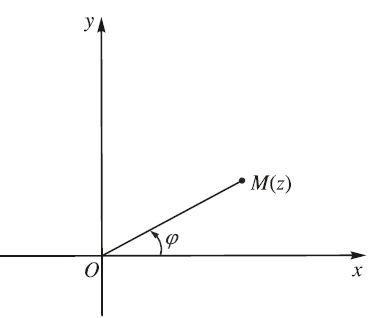
Cho số phức $z \neq 0$

Lúc này chúng ta gọi $M$ là điểm trong mặt phẳng phức biểu diễn số $z$

Số đo (ra-đi-an) của mỗi góc lượng giác tia đầu $O x$ và tia cuối $O M$ được gọi là một ác-gu-men của $z$

Ví dụ 7. Số phức $1+1i$ có một ác-gu-men là $\frac{\pi}{4}$

#11. Dạng lượng giác của số phức

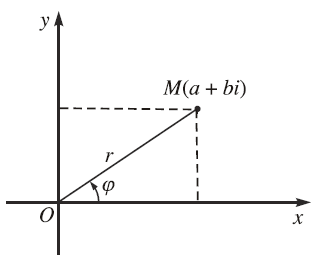
Dạng $z=r(\cos \varphi+i \sin \varphi)$ với $r>0$ được gọi là dạng lượng giác của số phức $z \neq 0$

Dạng $z=a+b i$ với $a, b \in \mathbb{R}$ được gọi là dạng đại số của số phức $z$

Để tìm dạng lượng giác $r(\cos \varphi+i \sin \varphi)$ của số phức $a+b i$ $(a, b \in \mathbb{R})$ khác $0$ cho trước chúng ta thực hiện tuần tự theo các chỉ dẫn bên dưới.

Tìm $r$ biết $r$ là mô đun của $z$ và được tính theo công thức $r=\sqrt{a^2+b^2}$

Tìm $\varphi$ biết $\varphi$ là một ác-gu-men của $z$

$\varphi$ là số thực sao cho $\cos \varphi=\frac{a}{r}$ và $\sin \varphi=\frac{b}{r}$

Ví dụ 8. Số $1+i$ có mô đun bằng $\sqrt{2}$ và có một ác-gu-men bằng $\frac{\pi}{4}$ nên nó có dạng lượng giác là $\sqrt{2}\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)$

#12. Nhân và chia số phức dưới dạng lượng giác

Việc nhân và chia hai số phức dưới dạng lượng giác đơn giản hơn nhân và chia số phức dưới dạng đại số.

Nếu $z=r(\cos \varphi+i \sin \varphi)$ và $z^{\prime}=r^{\prime}\left(\cos \varphi^{\prime}+i \sin \varphi^{\prime}\right)$ với $r \geq 0, r^{\prime} \geq 0$ thì …

• $z z^{\prime}=r r^{\prime}\left[\cos \left(\varphi+\varphi^{\prime}\right)+i \sin \left(\varphi+\varphi^{\prime}\right)\right]$
• $\frac{z^{\prime}}{z}=\frac{r^{\prime}}{r}\left[\cos \left(\varphi^{\prime}-\varphi\right)+i \sin \left(\varphi^{\prime}-\varphi\right)\right]$ với $r>0$

#13. Công thức Moa vrơ

Quy nạp Toán học công thức nhân số phức dưới dạng lượng giác chúng ta sẽ được công thức $[r(\cos \varphi+i \sin \varphi)]^n=r^n(\cos n \varphi+i \sin n \varphi)$ gọi là công thức Moa vrơ

Ví dụ 9. Tính $(1+i)^3$

Lời giải:

$(1+i)^3$

$=\left[\sqrt{2}\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)\right]^3$

$=(\sqrt{2})^3\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)$

$=2 \sqrt{2}\left(-\frac{\sqrt{2}}{2}+i \frac{\sqrt{2}}{2}\right)$

$=-2+2i$

#14. Căn bậc hai của số phức dưới dạng lượng giác

Xuất phát từ công thức Moa vrơ chúng ta dễ thấy số phức $z=r(\cos \varphi+i \sin \varphi)$ với $r>0$ có hai căn bậc hai là $\sqrt{r}\left(\cos \frac{\varphi}{2}+i \sin \frac{\varphi}{2}\right)$ và $\sqrt{r}\left(\cos \left(\frac{\varphi}{2}+\pi\right)+i \sin \left(\frac{\varphi}{2}+\pi\right)\right)$

Xem thêm:

• Cách tính lũy thừa và khai căn số phức (có nhiều ví dụ)
• Cách khai căn bậc n của số phức và bài tập ví dụ
• Chuyển số phức từ dạng đại số sang dạng lượng giác và ngược lại

#15. Lời kết

Vâng, trên đây là những công thức số phức thường gặp nhất.

Tuy mạch kiến thức về số phức là một mạch kiến thức mới nhưng việc tính toán với các số phức lại khá đơn giản, chỉ cần áp dụng công thức là xong.

Bằng cách này hay cách khác bạn hãy có gắng thuộc được các công thức vừa trình bày các bạn nhé.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn