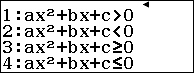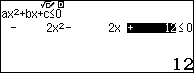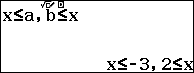2 cách giải bất phương trình bậc hai một ẩn, rất dễ

Trong bài viết trước chúng ta đã cùng nhau tìm hiểu cách giải bất phương trình bậc nhất một ẩn rồi.

Và để tiếp nối mạch kiến thức bất phương trình thì hôm nay chúng ta sẽ cùng nhau tìm hiểu cách giải bất phương trình bậc hai một ẩn.

Trong khuân khổ bài viết này mình lựa chọn hướng dẫn các cho bạn cách giải hai bất phương trình này vì nó rất thường gặp, có nhiều ứng dụng trong Toán học.

#1. Bất phương trình bậc hai một ẩn là gì?

Bất phương trình bậc hai một ẩn là bất phương trình có dạng $ax^2+bx+c<0$ hoặc $ax^2+bx+c>0$ hoặc $ax^2+bx+c \leq 0$ hoặc $ax^2+bx+c \geq 0$ (với $a, b, c$ là những số thức cho trước, $a$ khác $0$)

Ví dụ: $x^2-3x+2>0, x^2-2x+1<0, x^2+2x+3 \geq 0, -2x^2-2x+12 \leq 0$ là những bất phương trình bậc hai một ẩn.

#2. Kiến thức cần chuẩn bị

Để giải được phương trình bậc hai một ẩn bạn cần biết cách xét dấu tam thức bậc hai

Tất nhiên là cũng có những phương pháp, cũng như cách giải không cần biết mảng kiến thức trên nhưng đây là cách dễ nhất và được sử dụng nhiều nhất.

#3. Cách giải bất phương trình bậc hai một ẩn

Phương pháp #1. Dựa vào bảng xét dấu tam thức bậc hai tương ứng

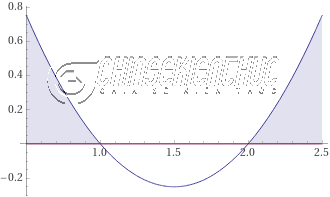
Ví dụ 1. Giải bất phương trình $x^2-3x+2>0$

Lời giải:

$f(x)=x^2-3x+2$ có hai nghiệm phân biệt $x_1=1, x_2=2$ và hệ số $a=1>0$

Ta có bảng xét dấu:

Vậy tập nghiệm của bất phương trình đã cho là $(-\infty, 1) \cup (2, +\infty)$

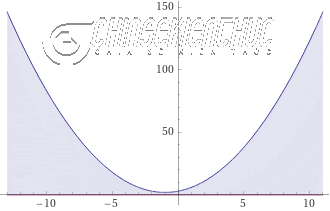
Ví dụ 2. Giải bất phương trình $x^2-2x+1<0$

Lời giải:

$g(x)=x^2-2x+1$ có một nghiệm kép duy nhất $x=1$ và hệ số $a=1>0$

Ta có bảng xét dấu:

Vậy tập nghiệm của bất phương trình đã cho là $\emptyset$ hay bất phương trình đã cho vô nghiệm

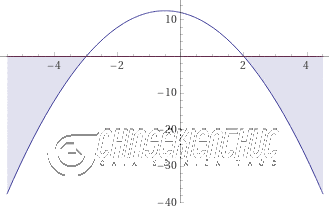
Ví dụ 3. Giải bất phương trình $x^2+2x+3 \geq 0$

Lời giải:

Cách 1: $h(x)=x^2+2x+3$ có $\Delta=-8<0$ và hệ số $a=1>0$ nên $h(x)>0$ với mọi $x \in (-\infty, +\infty)$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Vậy tập nghiệm của bất phương trình đã cho là $(-\infty, +\infty)$

Cách 2: $h(x)=x^2+2x+3=(x^2+2.x.1+1^2)+2=(x+1)^2+2>0$ với mọi $x \in (-\infty, +\infty)$

Vậy tập nghiệm của bất phương trình đã cho là $(-\infty, +\infty)$

Phương pháp #2. Sử dụng máy tính CASIO để giải

Ví dụ 4. Giải bất phương trình $-2x^2-2x+12 \leq 0$

Bước 1: Chọn phương thức tính toán Inequality

Bước 2: Chọn bậc của bất phương trình, ở phiên bản Casio FX-580VN X bạn có thể giải được đến bậc 4. Ở đây mình cần giải bất phương trình bậc 2 nên sẽ nhấn phím số 2

Bước 3: Chọn dấu của bất phương trình, ở đây mình cần giải bất phương trình $-2x^2-2x+12 \leq 0$ nên mình sẽ nhấn phím số 4

Bước 4: Nhập các hệ số của bất phương trình …

Bước 5: Nhấn phím = chúng ta sẽ thu được tập nghiệm của bất phương trình.

Vậy tập nghiệm của bất phương trình đã cho là $(-\infty, -3] \cup [2, +\infty)$

#4. Lời kết

Vâng, đến đây mình cũng đã hoàn thành mạch kiến thức về bất phương trình, cụ thể là cách giải bất phương trình bậc nhất một ẩn và cách giải bất phương trình bậc hai một ẩn rồi.

Một câu hỏi được đặt ra là nếu gặp các bất phương trình bậc cao hơn thì giải như thế nào?

Câu trả lời rất đơn giản, bạn chỉ cần lập bảng xét dấu tương ứng rồi dựa vào bảng xét dấu để tìm ra tập nghiệm thôi.

Đặc biệt, nếu nó là bất phương trình bậc ba, bậc bốn thì bạn có thể sử dụng phương thức tính toán Inequality trong máy tính CASIO fx-580VN X để giải nhanh hơn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com