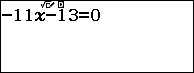2 cách giải bất phương trình bậc nhất một ẩn (có ví dụ)

Xin chào tất cả các bạn, trong bài viết ngày hôm nay chúng ta sẽ cùng nhau tìm hiểu cách giải bất phương trình bậc nhất một ẩn !

Đầu tiên chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tiếp theo là quy tắc chuyển vế và quy tắc nhân với một số khác 0 và cuối cùng là cách giải. Về quy trình thì là như vậy.

Với mỗi mục mình sẽ cho ví dụ minh họa tương ứng, việc làm này sẽ giúp các bạn dễ dàng tiếp thu kiến thức hơn

#1. Bất phương trình bậc nhất một ẩn là gì?

Bất phương trình bậc nhất một ẩn là bất phương trình có dạng $ax+b<0$ hoặc $ax+b>0$ hoặc $ax+b \leq 0$ hoặc $ax+b \geq 0$ (với $a, b$ là những số thực cho trước, $a \neq 0$)

Ví dụ: $2x+3>0, -5x+7<0, -11x-13 \leq 0$ là những bất phương trình bậc nhất một ẩn (ẩn ở đây là x).

#2. Quy tắc cần nhớ khi giải bất phương trình bậc nhất một ẩn

2.1. Quy tắc chuyển vế

Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia, ta phải đổi dấu hạng tử đó.

Ví dụ 1. Giải bất phương trình $x+3>0$

Lời giải:

$x+3>0 \Leftrightarrow x>-3$

Vậy tập nghiệm của bất phương trình đã cho là $\{x|x>-3\}$

Ở đây chúng ta đã chuyển hạng tử 3 của bất phương trình từ vế trái sang vế phải => nên đổi dấu thành -3

2.2. Quy tắc nhân với một số khác 0

Khi nhân hai vế của bất phương trình với cùng một số khác 0 ta phải:

• Giữ nguyên chiều của bất phương trình nếu như số đó là số dương.
• Đổi chiều bất phương trình, nếu như số đó là số âm.

Ví dụ 2. Giải bất phương trình $2x>-3$

Lời giải:

$2x>-3 \Leftrightarrow 2x.\frac{1}{2}>-3.\frac{1}{2} \Leftrightarrow x>-\frac{3}{2}$

Vậy tập nghiệm của bất phương trình đã cho là $\{x|x>-\frac{3}{2}\}$

Ở đây chúng ta đã nhân hai vế của bất phương trình với $\frac{1}{2}$. Dấu của bất phương trình > vẫn được giữ nguyên vì $\frac{1}{2}$ là một số dương

Ví dụ 3. Giải bất phương trình $-5x<-7$

Lời giải:

$-5x<-7 \Leftrightarrow -5x.\frac{-1}{5}>-7.\frac{-1}{5} \Leftrightarrow x>\frac{7}{5}$

Vậy tập nghiệm của bất phương trình đã cho là $\{x|x>\frac{7}{5}\}$

Ở đây chúng ta đã nhân hai vế của bất phương trình với $\frac{-1}{5}$. Dấu của bất phương trình < đổi thành > vì $\frac{-1}{5}$ là một số âm.

#3. Cách giải bất phương trình bậc nhất một ẩn

Ví dụ 4. Giải bất phương trình $2x+3>0$ và biểu diễn tập nghiệm trên trục số

Lời giải:

$2x+3>0$

$\Leftrightarrow 2x>-3$ (hạng tử +3 không chứa ẩn x nên được chuyển sang vế phải và đổi dấu thành -3)

$\Leftrightarrow 2x.\frac{1}{2}>-3.\frac{1}{2}$ (2 là hệ số của hạng tử chứa ẩn x, nghịch đảo của nó là $\frac{1}{2}$ và $\frac{1}{2}$ là số dương nên dấu > được giữ nguyên)

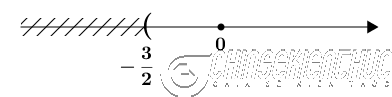
$\Leftrightarrow x>-\frac{3}{2}$ (thu gọn)

Vậy tập nghiệm của bất phương trình đã cho là $\{x|x>-\frac{3}{2}\}$

Chú ý: Khi trình bày lời giải bạn không cần ghi các câu giải thích như bên trên đâu nhé, ở đây mình ghi để các bạn dễ hiểu mà thôi.

Ví dụ 5. Giải bất phương trình $-5x+7<0$ và biểu diễn tập nghiệm trên trục số.

Lời giải:

$-5x+7<0$

$\Leftrightarrow -5x<-7$

$\Leftrightarrow -5x.\frac{-1}{5}>-7.\frac{-1}{5}$

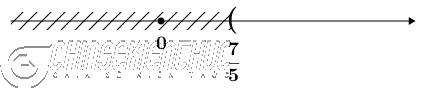
$\Leftrightarrow x>\frac{7}{5}$

Vậy tập nghiệm của bất phương trình đã cho là $\{x|x>\frac{7}{5}\}$

#4. Cách giải nhanh bất phương trình bậc nhất một ẩn bằng máy tính CASIO

NOTE:
Máy tính CASIO được mình sử dụng trong bài viết này là FX-580VN X, nếu các bạn sử dụng các dòng máy khác (FX-570EX Plus, FX-570VN Plus) thì các thao tác thực hiện vẫn tương tự nhé.

Giả sử ta cần giải bất phương trình $-11x-13 \leq 0$

Bước 1: Xác định dấu của tập nghiệm dựa vào dấu của hệ số đứng trước ẩn.

Vì hệ số đứng trước ẩn là $-11<0$ nên dấu của tập nghiệm đổi chiều tức dấu $\geq$

Bước 2: Giải phương trình tương ứng, ở đây là phương trình bậc nhất một ẩn $-11x-13 = 0$

Vậy tập nghiệm của bất phương trình đã cho là $\{x|x\geq-\frac{13}{11}\}$

#5. Lời kết

Vâng, trên đây là khái niệm về bất phương trình bậc nhất một ẩn, cũng như cách giải loại bất phương trình này.

Về cơ bản thì bất phương trình bậc nhất một ẩn tuy là đơn giản nhưng nó lại là một trong những bất phương trình có rất nhiều ứng dụng trong Toán học, cũng như trong thực tiễn.

Tiêu biểu như giải hệ bất phương trình bậc nhất, bài toán quy hoạch tuyến tính, bài toán tối ưu hóa, …

Vậy nên bạn cần dành sự quan tâm nhất định đến loại bất phương trình này, đặc biệt là không được quên cách giải bạn nhé. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách giải bất phương trình bậc nhất hai ẩn (có ví dụ)
• 7 cách giải phương trình bậc hai đơn giản, hiệu quả
• 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn
• Cách vẽ đồ thị hàm số bậc nhất (trên giấy & trên máy tính)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com