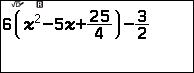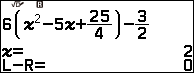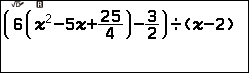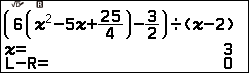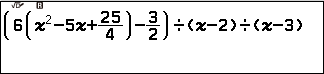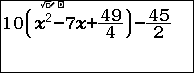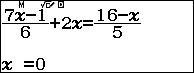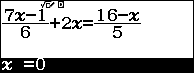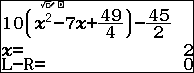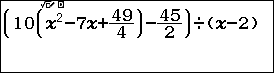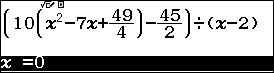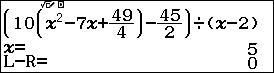Dò tìm tất cả các nghiệm của phương trình bằng CASIO

Như các bạn đều đã biết, tính năng Solver của máy tính Casio chỉ tìm được một nghiệm ngay cả khi phương trình đó có nhiều nghiệm, nó sẽ tìm ra nghiệm nào sẽ phụ thuộc vào giá trị x ban đầu

Giá trị x ban đầu là giá trị mà chúng ta sẽ nhập vào để máy tính CASIO bắt đầu dò tìm nghiệm, nghiệm nào gần giá trị x ban đầu hơn sẽ được ưu tiên hiển thị.

Vì chúng ta không biết giá trị của nghiệm là bao nhiêu nên thường nhập ngẫu nhiên một giá trị thuộc tập xác định, thường thường là nhập 0

Và để tìm được các nghiệm khác thì bạn cần phải nhập một giá trị x ban đầu khác.

Tuy nhiên, trong nhiều trường hợp thì điều này là không khả quan, máy tính CASIO vẫn chỉ xuất ra nghiệm đã tìm được trước đó.

Vậy làm thế nào để xử lý vấn đề này?

Vâng, biết được khó khăn đó thì hôm nay, mình sẽ hướng dẫn cho các bạn chi tiết các bước dò tìm tất cả các nghiệm của phương trình bằng máy CASIO.

#1. Cách tìm tất cả các nghiệm của phương trình trên Casio FX 880 BTG

NOTE:
Nếu chưa có máy tính Casio này thì bạn có thể đặt mua chính hãng tại đây hoặc tại đây !

Ví dụ 1. Dò tìm tất cả các nghiệm của phương trình $6\left(x^2-5x+\frac{25}{4}\right)=\frac{3}{2}$

Dễ thấy, phương trình đã cho tương đương với: $6\left(x^2-5x+\frac{25}{4}\right)-\frac{3}{2}=0$

Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK

Bước 2. Nhập vế trái của phương trình: $6\left(x^2-5x+\frac{25}{4}\right)-\frac{3}{2}=0$

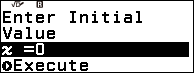
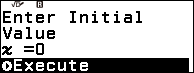
Bước 3. Nhấn phím EXE => nhập giá trị x ban đầu (x ban đầu là một số bất kì thuộc tập xác định của phương trình) mình thường nhập 0 => rồi nhấn phím EXE => nhấn phím EXE

Bước 4. Nhấn phím  => nhấn phím => nhập (phương trình) $\div$ (x – nghiệm vừa tìm được).

Bước 5. Nhấn phím EXE => nhập giá trị x ban đầu (x ban đầu là một số bất kì thuộc tập xác định của phương trình) mình thường nhập 0 => nhấn phím EXE => nhấn phím EXE’

Vậy => phương trình đã cho có tập nghiệm là {2, 3}

Nhưng một câu hỏi được đặt ra là tại sao mình biết phương trình đã cho có hai nghiệm để dừng quá trình dò tìm lại?

Quan sát phương trình đã cho chúng ta dễ dàng thấy được nó là phương trình quy về phương trình bậc hai, mà phương trình bậc hai thì có không quá hai nghiệm.

Trường bạn không nhìn thấy nó là phương trình quy về được phương trình bậc hai thì bạn hãy chia tiếp tục cho (x-3)

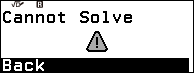
Tiếp tục chia cho đến khi xuất hiện thông báo Cannot Solve.

Xem video thao tác

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

#2. Cách Solver tất cả nghiệm của phương trình trên Casio FX 580 VN X

Ví dụ 2. Dò tìm tất cả các nghiệm của phương trình $10\left(x^2-7x+\frac{49}{4}\right)=\frac{45}{2}$

Dễ thấy, phương trình đã cho tương đương với: $10\left(x^2-7x+\frac{49}{4}\right)-\frac{45}{2}=0$

Bước 1. Nhập vế trái của phương trình $10\left(x^2-7x+\frac{49}{4}\right)-\frac{45}{2}=0$

Bước 2. Nhấn phím SHIFT => nhấn phím CALC

Bước 3. Nhập giá trị x ban đầu (x ban đầu là một số bất kì thuộc tập xác định của phương trình) mình thường nhập 0 => nhấn phím = => nhấn phím =

Bước 4. Nhấn phím => nhập (phương trình) $\div$ (x – nghiệm vừa tìm được)

Bước 5. Nhấn phím SHIFT => nhấn phím CALC

Bước 6. Nhập giá trị x ban đầu (x ban đầu là một số bất kì thuộc tập xác định của phương trình) mình thường nhập 0 => nhấn phím = => nhấn phím =

Lập luận như trong phần #1 chúng ta đi đến được kết luận phương trình đã cho có tập nghiệm là {2, 5}.

Xem video thao tác

# 3. Lời kết

Vâng, như vậy là mình đã hướng dẫn xong cho bạn cách dò tìm (solver) tất cả các nghiệm của phương trình bằng CASIO rồi nhé.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Solver nghiệm của phương trình bằng máy CASIO
• Cách tìm nghiệm của phương trình chứa tham số bằng Casio
• Chuyển đổi nghiệm thập phân sang căn thức bằng CASIO
• Chuyển đổi nghiệm thập phân sang nghiệm phân số bằng Casio

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn