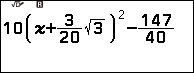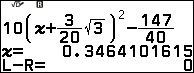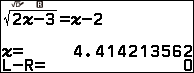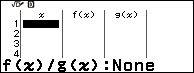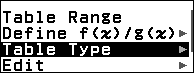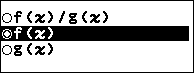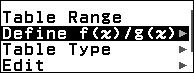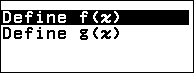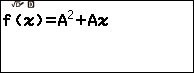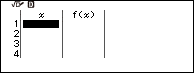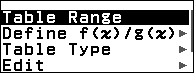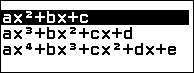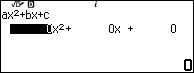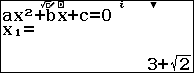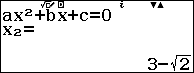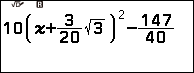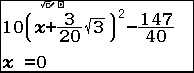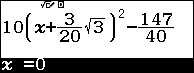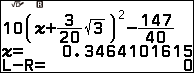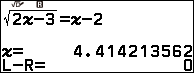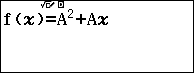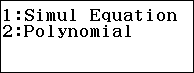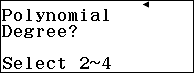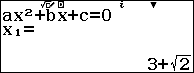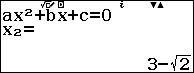Hello các bạn. Tính năng Solver của máy tính CASIO cho phép chúng ta dò tìm nghiệm của một phương trình bất kì.
Như các bạn đã biết, Solver là một trong những tính năng rất quan trọng trên máy tính cầm tay Casio. Hỗ trợ rất đắc lực trong quá trình giải toán.
Mục Lục Nội Dung
I. Tính năng Solver trên Casio có thể làm được gì?
Dưới đây là một số tính năng của Solver trên máy tính cầm tay Casio:
- Tính toán đa biến: Solver trên máy tính Casio cho phép tính toán đa biến, có nghĩa là nó có thể giải các bài toán có nhiều biến độc lập.
- Tìm giá trị cực đại và cực tiểu: Solver có thể tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số, cho phép người dùng giải được các bài toán tối ưu hóa.
- Hỗ trợ các phép tính: Solver hỗ trợ các phép tính cơ bản như cộng, trừ, nhân, chia và các phép tính toán khác như lũy thừa, căn bậc hai, hàm logarit và hàm mũ.
- Giải phương trình: Solver có thể giải các phương trình đại số, phương trình bậc hai và phương trình lượng giác.
- Giải hệ phương trình: Solver cũng có thể giải các hệ phương trình tuyến tính và phi tuyến.
- Tính toán chính xác: Solver trên máy tính Casio sử dụng tính toán chính xác để đảm bảo kết quả đúng.
- Tính toán nhanh: Với tốc độ xử lý nhanh, Solver trên máy tính cầm tay Casio giúp người dùng tiết kiệm thời gian khi giải các bài toán phức tạp.
Tóm lại, Solver trên máy tính cầm tay Casio là một tính năng rất hữu ích và đa năng, giúp người dùng (học sinh, sinh viên, giáo viên) giải quyết các bài toán phức tạp một cách nhanh chóng và chính xác.
Tùy thuộc vào từng loại phương trình mà máy tính CASIO sẽ cho ra nghiệm tương ứng. Về cơ bản có 4 loại nghiệm:
- Nghiệm nguyên.
- Nghiệm thập phân hữu hạn và nghiệm thập phân vô hạn tuần hoàn (phân số).
- Nghiệm thập phân vô hạn không tuần hoàn (căn thức).
- Nghiệm siêu việt ($\pi$, e).
Trong hấu hết các trường hợp, chỉ có loại đầu tiên có thể sử dụng ngay, ba loại còn lại cần phải xử lí thêm.
Trong bài viết này, mình sẽ hướng dẫn xử lí loại thứ ba tức chuyển nghiệm thập phân vô hạn không tuần hoàn sang căn thức bằng máy tính CASIO.
II. Các bước chuyển đổi nghiệm thập phân sang căn thức bằng CASIO
Bước 1. Sử dụng tính năng Solver dò tìm nghiệm.
Bước 2. Gán nghiệm vừa tìm được vào biến nhớ A.
Bước 3. Sử dụng phím bình phương, khai căn và biến nhớ A để máy tính CASIO chuyển tự động.
Nếu nghiệm vừa tìm được có dấu trừ thì cần thêm dấu trừ khi kết luận nghiệm của phương trình.
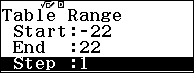
Bước 4. Sử dụng tính năng tạo bảng giá trị với f(x) là $A^2+Ax$ và Start = -22, End = 22, Step = 1
Bước 5. Giả sử $f(x_0)$ là một giá trị nguyên, lúc bấy giờ A sẽ là nghiệm của phương trình bậc hai $x^2+x_0x-f(x_0)=0$
Bước 6. Sử dụng tính năng Equation (Polynomial) giải phương trình $x^2+x_0x-f(x_0)=0$
NOTE:
Chúng ta chỉ thực hiện Bước 4, Bước 5 và Bước 7 khi Bước 3 không khả dụng.
#1. Thực hành trên Casio FX 880 BTG
Đọc thêm:
Bài tập ví dụ về chuyển nghiệm thập phân sang căn thức
Ví dụ 1. Dò tìm một nghiệm của phương trình $10\left(x+\frac{3}{20}\sqrt{3}\right)^2-\frac{147}{40}=0$
Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK.
Bước 2. Nhập vế trái phương trình đã cho
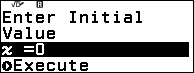
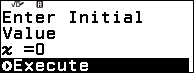
Bước 3. Nhấn phím EXE => nhập giá trị x ban đầu (x ban đầu là một số bất kì thuộc tập xác định của phương trình) mình thường nhập 0 => nhấn phím EXE => nhấn phím EXE
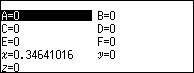
Bước 4. Nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK
Bước 5. Nhấn phím HOME => chọn Calculate => nhấn phím OK
Bước 6. Nhập $\sqrt{A^2}$ => nhấn phím EXE
Vậy một nghiệm của phương trình đã cho là $\frac{\sqrt{3}}{5}$
Ví dụ 2. dò tìm nghiệm một của trình $\sqrt{2x-3}=x-2$
Bạn thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta thu được nghiệm thập phân.
Tiếp tục thực hiện Bước 4, Bước 5 và Bước 6 để chuyển nghiệm thập phân sang nghiệm phân số nhưng không thành công.
Suy ra máy tính CASIO không chuyển tự động được, lúc bấy giờ chúng ta phải giúp nó
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
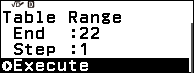
Bước 7. Tạo bảng giá trị cho hàm số $A^2+Ax$ với Start = -22, End = 22, Step = 1
Bước 7.1. Nhấn phím HOME => chọn Table => nhấn phím OK
Bước 7.2. Nhấn phím TOOLS => chọn Table Type => nhấn phím OK => chọn f(x) => nhấn phím OK => nhấn phím AC
Bước 7.3. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK => nhập $A^2+Ax$ => nhấn phím EXE
Bước 7.4. Nhấn phím TOOLS => chọn Table Range => nhấn phím OK => nhập -22 => nhấn phím OK => nhập 22 => nhấn phím OK => nhập 1 => nhấn phím OK => nhấn phím OK
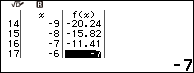
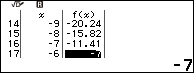
Quan sát cột f(x) và cố gắng tìm một giá trị nguyên, dễ thấy f(-6) là một giá trị nguyên.
Lúc này nghiệm của phương trình vô tỉ đã cho cũng là nghiệm của phương trình bậc hai $x^2-6x+7=0$
NOTE:
Có vô số phương trình bậc hai nhận nghiệm của phương trình vô tỉ làm nghiệm, nhưng không phải lúc nào chúng ta cũng tìm được một cách dễ dàng.
Bước 8. Sử dụng tính năng Equation (Polynomial) để giải phương trình $x^2-6x+7=0$
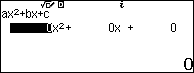
Bước 8.1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK
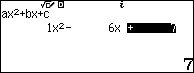
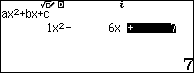
Bước 8.2. Nhập 1 => nhấn phím EXE => nhập -6 => nhấn phím EXE => nhập 7=> nhấn phím EXE
Bước 8.3. Nhấn phím EXE => nhấn phím EXE
Mặc dù phương trình $x^2-6x+7=0$ có hai nghiệm nhưng chúng ta dễ dàng phân biệt được đâu là nghiệm của phương trình vô tỉ đã cho.
Vậy một nghiệm của phương trình đã cho là $3+\sqrt{2}$
Xem video bấm máy Casio FX-880 BTG
#2. Thực hành trên Casio FX 580 VN X
Ví dụ 1. Dò tìm một nghiệm của phương trình $10\left(x+\frac{3}{20}\sqrt{3}\right)^2-\frac{147}{40}=0$
Bước 1. Nhập vế trái phương trình đã cho.
Bước 2. Nhấn phím SHIFT => nhấn phím CALC
Bước 3. Nhấn phím EXE => nhập giá trị x ban đầu (x ban đầu là một số bất kì thuộc tập xác định của phương trình) mình thường nhập 0 => nhấn phím = => nhấn phím =
Bước 4. Nhấn phím STO => nhấn phím (-)
Bước 5. Nhập $\sqrt{A^2}$ => nhấn phím =
Vậy một nghiệm của phương trình đã cho là $\frac{\sqrt{3}}{5}$
Ví dụ 2. Dò tìm nghiệm một của trình $\sqrt{2x-3}=x-2$
Thực hiện tương tự Bước 1 đến Bước 3 của Ví dụ 1 chúng ta thu được nghiệm thập phân.
Tiếp tục thực hiện Bước 4 và Bước 5 để chuyển nghiệm thập phân sang nghiệm phân số nhưng không thành công.
Vậy nên suy ra máy tính CASIO không chuyển tự động được, lúc bấy giờ chúng ta phải giúp nó.
Bước 6. Tạo bảng giá trị cho hàm số $A^2+Ax$ với Start = -22, End = 22, Step = 1
Bước 6.1. Nhấn phím SHIFT => nhấn phím MENU => nhấn phím => nhấn phím
=> nhấn phím 1 => nhấn phím 1
Bước 6.2. Nhấn phím MENU => chọn Table => nhấn phím =
Bước 6.3. Nhập $A^2+Ax$ => nhấn phím =
Bước 6.4. Nhập -22 => nhấn phím = => nhập 22 => nhấn phím = => nhập 1 => nhấn phím = => nhấn phím =
Quan sát cột f(x) và cố gắng tìm một giá trị nguyên, dễ thấy f(-6) là một giá trị nguyên
Lúc này nghiệm của phương trình vô tỉ đã cho cũng là nghiệm của phương trình bậc hai $x^2-6x+7=0$
Có vô số phương trình bậc hai nhận nghiệm của phương trình vô tỉ làm nghiệm nhưng không phải lúc nào chúng ta cũng tìm được một cách dễ dàng.
Bước 7. Sử dụng tính năng Equation / Func (Polynomial) để giải phương trình $x^2-6x+7=0$
Bước 7.1. Nhấn phím MENU => chọn Equation / Func => nhấn phím = => nhấn phím 2 => nhấn phím 2
Bước 7.2. Nhập 1 => nhấn phím = => nhập -6 => nhấn phím = => nhập 7 => nhấn phím =
Bước 7.3. Nhấn phím = => nhấn phím =
Mặc dù phương trình $x^2-6x+7=0$ có hai nghiệm nhưng chúng ta dễ dàng phân biệt được đâu là nghiệm của phương trình vô tỉ đã cho.
Vậy một nghiệm của phương trình đã cho là $3+\sqrt{2}$
Xem video bấm máy Casio FX-580 VNX
Xem thêm:
- Cách tạo bảng giá trị Table bằng CASIO
- Cách giải phương trình bậc 2, bậc 3 và bậc 4 bằng CASIO
- Chuyển đổi nghiệm thập phân sang nghiệm phân số bằng Casio
III. Lời kết
Như vậy là mình vừa hướng dẫn rất chi tiết cho bạn cách sử dụng máy tính Casio để chuyển đổi nghiệm thập phân sang nghiệm căn thức rồi nhé, cách làm tương đối đơn giản đúng không nào 🙂
Tuy nhiên, trong quá trình giải bài tập còn một số ít trường hợp nữa mà các chỉ dẫn trong bài viết này chưa giải quyết được.
Cụ thể, nếu nghiệm thập phân vô hạn không tuần hoàn có dạng $\frac{a+\sqrt{b}}{c}$ thì thủ thuật này sẽ không áp dụng được.
Lúc này, nếu bạn muốn chuyển được thì bạn cần phải chuyển nó sang “liên phân số” trước, tiếp theo chúng ta suy ra được phương trình bậc hai và cuối cùng là suy ra nghiệm.
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống