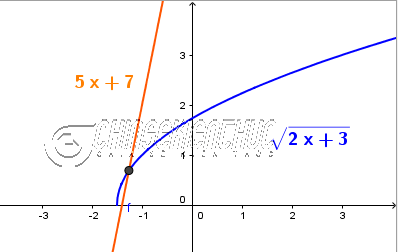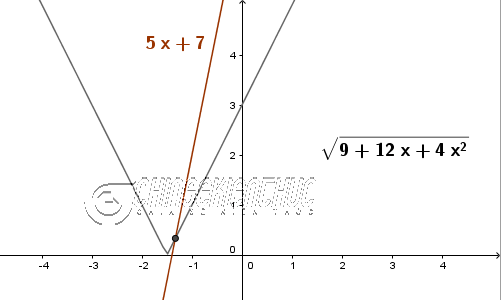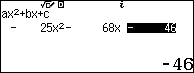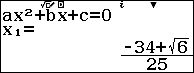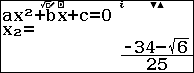2 cách giải phương trình vô tỉ (2 dạng thường gặp nhất)

Tương tự như phương trình chứa dấu giá trị tuyệt đối, phương trình vô tỉ cũng rất thường gặp trong chương trình Toán học Trung học, đặc biệt trong các kỳ thi học sinh giỏi.

Vậy nên hôm nay mình sẽ hướng dẫn cho các bạn cách giải hai dạng phương trình vô tỉ thường gặp nhất, đó là $\sqrt{f(x)}=g(x)$ và $\sqrt{f(x)}=\sqrt{g(x)}$

Hai dạng trên, ngoài thường gặp nhất ra thì nó còn dễ giải nhất nữa 🙂 nếu gặp các phương trình vô tỉ có dạng khác thì bạn hãy cố gắng biến đổi sơ cấp để đưa nó về hai dạng này nhé.

#1. Giải phương trình vô tỉ (sử dụng kiến thức Toán học)

Các kiến thức được trình bày bên dưới đây bản chất là các cách giải, bắt buộc bạn phải ghi nhớ ha.

Cách 1. Dựa vào định nghĩa căn thức

Cho $a$ là một số thức dương, lúc bấy giờ, số $\sqrt{a}$ được gọi là căn bậc hai số học của $a$

$\sqrt{a}=x \Leftrightarrow \left\{\begin{array}{l}x \geq 0 \\ a=x^2 \end{array}\right.$

Cách 2. Dựa vào mệnh đề tương đương

$\sqrt{f(x)}=g(x) \Leftrightarrow \left\{\begin{array}{l}g(x) \geq 0 \\ f(x)=[g(x)]^2 \end{array}\right.$

$\sqrt{f(x)}=\sqrt{g(x)} \Leftrightarrow \left\{\begin{array}{l}\left[\begin{array}{l}f(x) \geq 0 \\ g(x) \geq 0 \end{array}\right. \\ f(x)=g(x) \end{array}\right.$

#2. Bài tập ví dụ

Ví dụ 1. Giải phương trình $\sqrt{2x+3}=5x+7$

Lời giải:

Cách 1. Dựa vào định nghĩa căn thức

Điều kiện xác định của phương trình đã cho là $2x+3 \geq 0 \Leftrightarrow x \geq -\frac{3}{2}$

Bình phương hai vế của phương trình đã cho chúng ta được phương trình hệ quả $2x+3=(3x+7)^2$

$2x+3=(3x+7)^2 \Rightarrow 2x+3=25x^2+70x+49 \Rightarrow -25x^2-68x-46=0$

Phương trình bậc hai một ẩn vừa tìm được có hai nghiệm là $-\frac{34}{25}-\frac{\sqrt{6}}{25}, -\frac{34}{25}+\frac{\sqrt{6}}{25}$

Cả hai giá trị này đều thỏa mãn điều kiện của phương trình đã cho nhưng khi thay vào phương trình đã cho thì giá trị $-\frac{34}{25}-\frac{\sqrt{6}}{25}$ không thỏa, giá trị $-\frac{34}{25}+\frac{\sqrt{6}}{25}$ thỏa

Vậy nghiệm của phương trình đã cho là $-\frac{34}{25}+\frac{\sqrt{6}}{25}$

Cách 2. Dựa vào mệnh đề tương đương

$\sqrt{2x+3}=5x+7 \Leftrightarrow \left\{\begin{array}{l}5x+7 \geq 0 \\ 2x+3=(5x+7)^2 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{7}{5} \\ -25x^2-68x-46=0 \end{array}\right.\Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{7}{5} \\ \left[\begin{array}{l}x=-\frac{34}{25}-\frac{\sqrt{6}}{25} \\ x=-\frac{34}{25}+\frac{\sqrt{6}}{25} \end{array}\right. \end{array}\right. \Leftrightarrow x=-\frac{34}{25}+\frac{\sqrt{6}}{25}$

Vậy nghiệm của phương trình đã cho là $-\frac{34}{25}+\frac{\sqrt{6}}{25}$

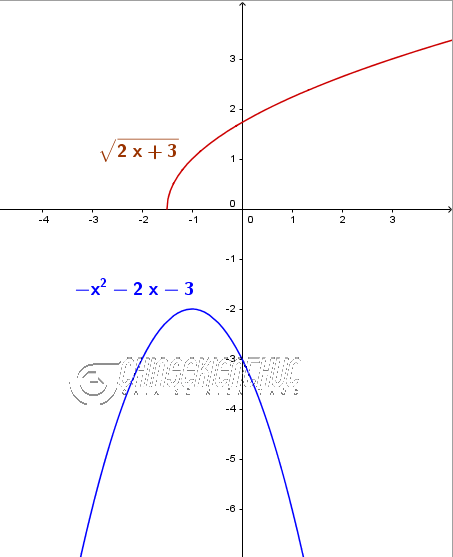
Ví dụ 2. Giải phương trình $\sqrt{2x+3}=-x^2-2x-3$

Lời giải:

$-x^2-2x-3=-(x^2+2x+3)=-(x^2+2.x.1+1^2+2)=-[(x+1)^2+2]=-(x+1)^2-2<0$ với mọi số thực $x$ bất kì

Vậy => phương trình đã cho vô nghiệm.

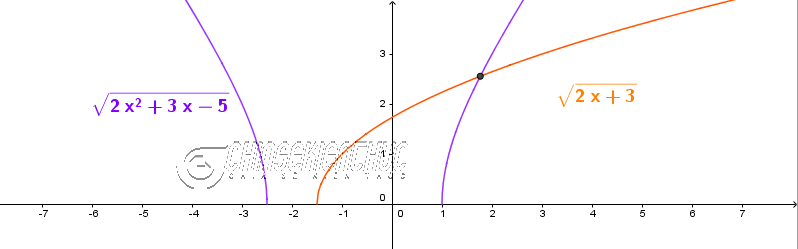
Ví dụ 3. Giải phương trình $\sqrt{2x+3}=\sqrt{2x^2+3x-5}$

Lời giải:

Cách 1. Dựa vào định nghĩa căn thức

Cách này không thực sự tối ưu với ví dụ này nên mình sẽ không trình bày ở đây, bạn có thể tự nghiên cứu thêm nếu muốn ha.

Cách 2. Dựa vào mệnh đề tương đương

$\sqrt{2x+3}=\sqrt{2x^2+3x-5} \Leftrightarrow \left\{\begin{array}{l}2x+3 \geq 0 \\ 2x+3=2x^2+3x-5 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{3}{2} \\ -2x^2-x +8=0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{3}{2} \\ \left[\begin{array}{l}x=-\frac{1}{4}-\frac{\sqrt{65}}{4} \\ x=-\frac{1}{4}+\frac{\sqrt{65}}{4} \end{array}\right. \end{array}\right.\Leftrightarrow x=-\frac{1}{4}+\frac{\sqrt{65}}{4}$

Vậy nghiệm của phương trình đã cho là $-\frac{1}{4}+\frac{\sqrt{65}}{4}$

Chú ý: Vì f(x) đơn giản hơn g(x) nên mình đã chọn điều kiện là $2x+3 \geq 0$ thay vì $2x^2+3x-5 \geq 0$

Ví dụ 4. Giải phương trình $\sqrt{9+12x+4x^2}=5x+7$

Lời giải:

Phương pháp 1: Giải trực tiếp phương trình vô tỉ

$\sqrt{9+12x+4x^2}=5x+7 \Leftrightarrow \left\{ \begin{array}{l} 5x+7 \geq 0 \\ 9+12x+4x^2=(5x+7)^2 \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} x \geq -\frac{7}{5} \\ -21x^2-58x-40=0 \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} x \geq -\frac{7}{5} \\ \left[ \begin{array}{l} x=-\frac{10}{7} \\ x=-\frac{4}{3} \end{array}\right. \end{array}\right. \Leftrightarrow x=-\frac{4}{3}$

Vậy phương trình đã cho có một nghiệm duy nhất là $x=-\frac{4}{3}$

Phương pháp 2: Chuyển về phương trình chứa dấu giá trị tuyệt đối

$\sqrt{9+12x+4x^2}=5x+7 \Leftrightarrow \sqrt{(3)^2+2.3.2x+(2x)^2}=5x+7 \Leftrightarrow \sqrt{(3+2x)^2}=5x+7 \Leftrightarrow |3+2x|=5x+7$

$|2x+3|=5x+7 \Leftrightarrow \left\{\begin{array}{l}5x+7 \geq 0 \\ \left[\begin{array}{l} 2x+3=5x+7 \\ 2x+3=-(5x+7) \end{array}\right.\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{7}{5} \\ \left[\begin{array}{l} -3x-4=0 \\ -7x-10=0 \end{array}\right.\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{7}{5} \\ \left[\begin{array}{l} x=-\frac{4}{3} \\ x=-\frac{10}{7} \end{array}\right.\end{array}\right. \Leftrightarrow x=-\frac{4}{3}$

#3. Chú ý về cách viết / hiển thị nghiệm của phương trình bậc hai

Cũng một phương trình bậc hai nhưng khi giải bằng kiến thức Toán học, giải bằng công cụ trực tuyến Wolfram Alpha, hoặc giải bằng máy tính CASIO fx-580VN X, …, có thể có các cách viết, cũng như cách hiển thị khác nhau.

Cụ thể thì nghiệm của phương trình $-25x^2-68x-46=0$ khi giải bằng:

+) Kiến thức Toán học Toán học…

$x_1=\frac{-68+\sqrt{24}}{-50}, x_2=\frac{-68-\sqrt{24}}{-50}$

+) Giải bằng công cụ Wolfram Alpha

+) Giải bằng máy tính CASIO Fx-580VN X

Cả ba trường hợp sẽ có ba cách viết / hiển thị khác nhau nhưng đều có cùng một giá trị, đều là một, đều là nghiệm của phương trình $-25x^2-68x-46=0$

#4. Lời kết

Vâng, như vậy là mình vừa hướng dân xong cho các bạn cách giải phương trình vô tỉ rồi ha.

Trong thực tế, khi gặp một phương trình vô tỉ có dạng khác, bạn hãy cố gắng biến đổi sơ cấp chuyển về hai dạng này, nếu không thể tùy thuộc vào dạng của phương trình mà cân nhắc lựa chọn phương pháp giải cho phù hợp

Dưới đây là một số phương pháp giải mà các bạn nên nghiên cứu thêm …

• Phương pháp nâng lên lũy thừa (hai cách được trình bày trong bài viết này thuộc phương pháp này)
• Phương pháp lượng liên hợp
• Phương pháp đặt ẩn phụ
• Phương pháp đánh giá
• Phương pháp lượng giác hóa

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

 CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn