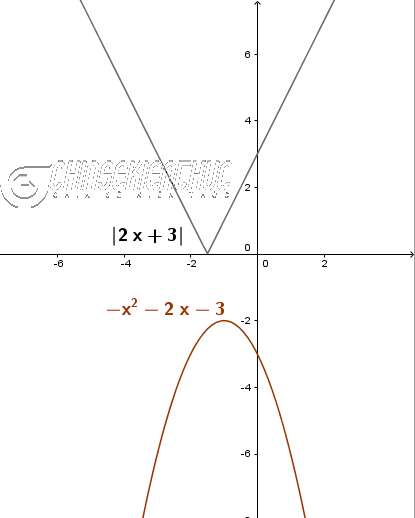3 cách giải phương trình chứa dấu giá trị tuyệt đối

Phương trình chứa dấu giá trị tuyệt đối là một trong những phương trình cơ bản của Đại số sơ cấp, vì là cơ bản nên rất thường gặp (đặc biệt là trong chương trình Toán học Trung học cơ sở). Vậy nên…

Hôm nay mình sẽ hướng dẫn với các bạn 3 cách giải phương trình chứa dấu giá trị tuyệt đối với hai dạng $|f(x)|=g(x)$ và $|f(x)|=|g(x)|$

Đây là hai dạng thường gặp nhất, nếu gặp các dạng khác bạn chỉ cần biến đổi sơ cấp đưa về hai dạng này là được ha.

I. Giải phương trình chứa dấu giá trị tuyệt đối 

Các kiến thức được trình bày bên dưới bản chất là các cách giải, bắt buộc phải ghi nhớ các bạn nhá.

Cách #1. Dựa vào định nghĩa giá trị tuyệt đối

Giá trị tuyệt đối của một số a được kí hiệu là |a| và $|a|=\left\{\begin{array}{l}a~khi~a \geq 0 \\ -a~khi~a<0 \end{array}\right.$

Cách #2. Dựa vào mệnh đề tương đương

$|f(x)|=g(x) \Leftrightarrow \left\{\begin{array}{l}g(x) \geq 0 \\ \left[\begin{array}{l} f(x)=g(x) \\ f(x)=-g(x)\end{array}\right.\end{array}\right.$

Chú ý:
Nếu chứng minh được $g(x)<0$ thì phương trình lập tức vô nghiệm

$|f(x)|=|g(x)| \Leftrightarrow \left[\begin{array}{l} f(x)=g(x) \\ f(x)=-g(x)\end{array}\right.$

Cách #3. Dựa vào bảng xét dấu

Nếu bạn lựa chọn cách này để giải phương trình chứa dấu giá trị tuyệt đối thì bạn cần phải xem lại cách xét dấu nhị thức, cách xét dấu tam thức trước ha.

Xem thêm: Cách lập bảng xét dấu tự động bằng phần mềm Geophar

II. Bài tập ví dụ

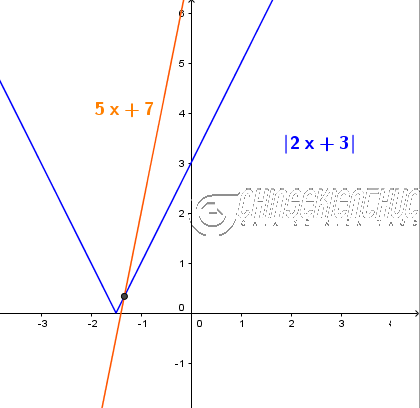
Ví dụ 1. Giải phương trình $|2x+3|=5x+7$

Lời giải:

Cách 1. Dựa vào định nghĩa giá trị tuyệt đối

Dễ thấy:

• $|2x+3|=2x+3$ khi $2x+3 \geq 0 \Leftrightarrow x \geq -\frac{3}{2}$
• $|2x+3|=-(2x+3)$ khi $2x+3 < 0 \Leftrightarrow x < -\frac{3}{2}$

Vậy suy ra, để giải được phương trình $|2x+3|=5x+7$ thì chúng ta cần giải phương trình $2x+3=5x+7$ và $-(2x+3)=5x+7$

Trường hợp 1: Với điều kiện $x \geq -\frac{3}{2}$ phương trình $|2x+3|=5x+7$  cho trở thành $2x+3=5x+7$

Giải phương trình $2x+3=5x+7 \Leftrightarrow -3x-4=0 \Leftrightarrow x=-\frac{4}{3}$

$x=-\frac{4}{3}$ thỏa mãn điều kiện $x \geq -\frac{3}{2}$ nên $x=-\frac{4}{3}$ là nghiệm của phương trình đã cho

Trường hợp 2: Với điều kiện $x < -\frac{3}{2}$ phương trình $|2x+3|=5x+7$  cho trở thành $-(2x+3)=5x+7$

Giải phương trình $-(2x+3)=5x+7 \Leftrightarrow -7x-10=0 \Leftrightarrow x=-\frac{10}{7}$

$x=-\frac{10}{7}$ không thỏa mãn điều kiện $x < -\frac{3}{2}$ nên $x=-\frac{10}{7}$ không là nghiệm của phương trình đã cho

Vậy phương trình đã cho có một nghiệm duy nhất là $x=-\frac{4}{3}$

Cách 2. Dựa vào mệnh đề tương đương

$|2x+3|=5x+7 \Leftrightarrow \left\{\begin{array}{l}5x+7 \geq 0 \\ \left[\begin{array}{l} 2x+3=5x+7 \\ 2x+3=-(5x+7) \end{array}\right.\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{7}{5} \\ \left[\begin{array}{l} -3x-4=0 \\ -7x-10=0 \end{array}\right.\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \geq -\frac{7}{5} \\ \left[\begin{array}{l} x=-\frac{4}{3}~(nhận)\\ x=-\frac{10}{7}~(loại) \end{array}\right.\end{array}\right.$

Vậy phương trình đã cho có một nghiệm duy nhất là $x=-\frac{4}{3}$

Cách 3. Dựa vào bảng xét dấu

Đối với  ví dụ này thì cách dựa vào bảng xét dấu không phải là cách tối ưu, vậy nên mình sẽ bỏ qua cách này các bạn nhé.

Ví dụ 2. Giải phương trình $|2x+3|=-x^2-2x-3$

Lời giải:

$-x^2-2x-3=-(x^2+2x+3)=-(x^2+2.x.1+1^2+2)=-[(x+1)^2+2]=-(x+1)^2-2<0$ với mọi số thực x bất kỳ

Vì vế trái của phương trình luôn âm nên phương trình đã cho vô nghiệm.

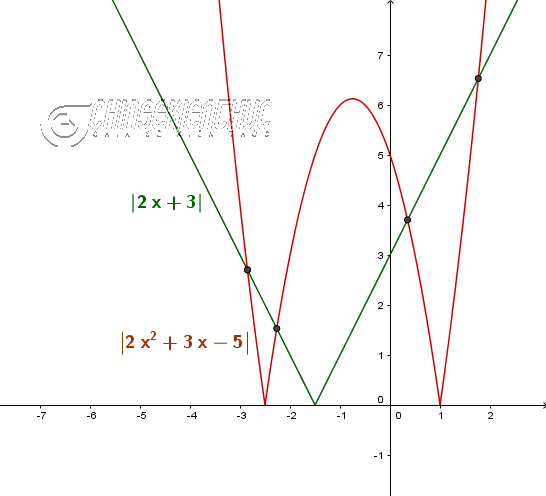
Ví dụ 3. Giải phương trình $|2x+3|=|2x^2+3x-5|$

Lời giải:

Cách 1. Dựa vào định nghĩa giá trị tuyệt đối.

Cách dựa vào định nghĩa giá trị tuyệt đối không tối ưu đối với ví dụ này vì phải xét khá nhiều trường hợp. Vậy nên mình sẽ bỏ qua, không trình bày lời giải cho cách này.

Cách 2. Dựa vào mệnh đề tương đương

$|2x+3|=|2x^2+3x-5| \Leftrightarrow \left[\begin{array}{l} 2x+3=2x^2+3x-5 \\ 2x+3=-(2x^2+3x-5) \end{array}\right. \Leftrightarrow \left[\begin{array}{l} -2x^2-x+8=0 \\ 2x^2+5x-2=0 \end{array}\right. \Leftrightarrow \left[\begin{array}{l} \left[\begin{array}{l}x=-\frac{1}{4}-\frac{\sqrt{65}}{4} \\ x=\frac{\sqrt{65}}{4}-\frac{1}{4} \end{array}\right. \\ \left[\begin{array}{l}x=-\frac{5}{4}-\frac{\sqrt{41}}{4} \\ x=\frac{\sqrt{41}}{4}-\frac{5}{4} \end{array}\right.\end{array}\right.$

Vậy phương trình đã cho có bốn nghiệm là $-\frac{1}{4}-\frac{\sqrt{65}}{4}, \frac{\sqrt{65}}{4}-\frac{1}{4}, -\frac{5}{4}-\frac{\sqrt{41}}{4}, \frac{\sqrt{41}}{4}-\frac{5}{4}$

Cách 3. Dựa vào bảng xét dấu

Dễ thấy:

• $x=-\frac{3}{2}$ là nghiệm của phương trình $2x+3=0$
• $x=-\frac{5}{2}, x=1$ là nghiệm của phương trình $2x^2+3x-5=0$

Chúng ta lập bảng xét dấu như hình bên dưới …

Lúc này chúng ta sẽ xét từng trường hợp để bỏ dấu giá trị tuyệt đối.

Trường hợp 1. với $x<-\frac{5}{2}$ phương trình đã cho trở thành $-(2x+3)=2x^2+3x-5 \Leftrightarrow -2x^2-5x+2=0$

Phương trình $-2x^2-5x+2=0$ có hai nghiệm là $-\frac{5}{4}-\frac{\sqrt{41}}{4}$ (nhận), $\frac{\sqrt{41}}{4}-\frac{5}{4}$ (loại)

Trường hợp 2. với $-\frac{5}{2} \leq x \leq -\frac{3}{2}$ phương trình đã cho trở thành $-(2x+3)=-(2x^2+3x-5) \Leftrightarrow 2x^2+x-8=0$

Phương trình $2x^2+x-8=0$ có hai nghiệm là $-\frac{1}{4}-\frac{\sqrt{65}}{4}$ (nhận), $\frac{\sqrt{65}}{4}-\frac{1}{4}$ (loại)

Trường hợp 3. với $-\frac{3}{2} < x \leq 1$ phương trình đã cho trở thành $2x+3=-(2x^2+3x-5) \Leftrightarrow 2x^2+5x-2=0$

Phương trình $2x^2+5x-2=0$ có hai nghiệm là $-\frac{5}{4}-\frac{\sqrt{41}}{4}$ (loại), $\frac{\sqrt{41}}{4}-\frac{5}{4}$ (nhận)

Trường hợp 4. với $x>1$ phương trình đã cho trở thành $2x+3=2x^2+3x-5 \Leftrightarrow -2x^2-x+8=0$

Phương trình $-2x^2-x+8=0$ có hai nghiệm là $-\frac{1}{4}-\frac{\sqrt{65}}{4}$ (loại), $\frac{\sqrt{65}}{4}-\frac{1}{4}$ (nhận)

Vậy phương trình đã cho có bốn nghiệm là $-\frac{1}{4}-\frac{\sqrt{65}}{4}, \frac{\sqrt{65}}{4}-\frac{1}{4}, -\frac{5}{4}-\frac{\sqrt{41}}{4}, \frac{\sqrt{41}}{4}-\frac{5}{4}$

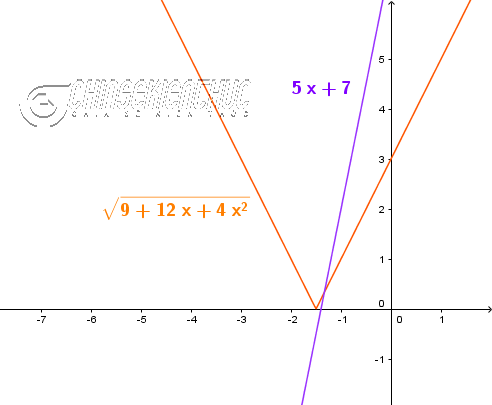
Ví dụ 4. Giải phương trình $\sqrt{9+12x+4x^2}=5x+7$

Thoạt nhìn thì chúng ta cứ tưởng phương trình đã cho là một phương trình vô tỉ, nhưng thật ra nó có thể biểu diễn dưới dạng phương trình có dấu giá trị tuyệt đối đó các bạn.

Lời giải:

Phương pháp 1. Chuyển về phương trình chứa dấu giá trị tuyệt đối.

$\sqrt{9+12x+4x^2}=5x+7 \Leftrightarrow \sqrt{(3)^2+2.3.2x+(2x)^2}=5x+7 \Leftrightarrow \sqrt{(3+2x)^2}=5x+7 \Leftrightarrow |3+2x|=5x+7$

Phần lời giải tiếp theo giống hệt Ví dụ 1

Phương pháp 2. Giải phương trình vô tỉ

$\sqrt{9+12x+4x^2}=5x+7 \Leftrightarrow \left\{ \begin{array}{l} 5x+7 \geq 0 \\ 9+12x+4x^2=(5x+7)^2 \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} x \geq -\frac{7}{5} \\ -21x^2-58x-40=0 \end{array}\right. \Leftrightarrow \left\{ \begin{array}{l} x \geq -\frac{7}{5} \\ \left[ \begin{array}{l} x=-\frac{10}{7}~(loại) \\ x=-\frac{4}{3}~(nhận) \end{array}\right. \end{array}\right.$

Vậy phương trình đã cho có một nghiệm duy nhất là $x=-\frac{4}{3}$

III. Lời kết

Okay, trên đây là phần hướng dẫn của mình về cách giải phương trình chứa dấu giá trị tuyệt đối.

Tùy thuộc vào phương trình chứa dấu giá trị tuyệt đối cụ thể mà chúng ta sẽ cân nhắc lựa chọn phương pháp sao cho tối ưu nhất, linh hoạt nhất.

Dưới đây là một số gợi ý / kinh nghiệm của mình muốn gửi đến các bạn:

• Cách 1 phù hợp với học sinh có học lực trung bình.
• Cách 2 phù hợp với học sinh có học lực khá, muốn sử dụng được cách này bắt buộc phải nhớ được các mệnh đề tương đương.
• Cách 3 phù hợp với học sinh có học lực khá, cách này đặc biệt thích hợp với những phương trình chứa nhiều dấu giá trị tuyệt đối.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn