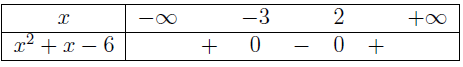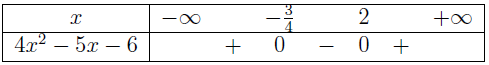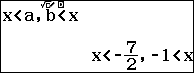2 cách giải hệ bất phương trình bậc hai một ẩn (nhiều ví dụ)

Hôm nay, mình sẽ tiếp tục hướng dẫn cho các bạn cách giải hệ bất phương trình bậc hai một ẩn.

Muốn giải được hệ bất phương trình này một cách nhanh chóng và chính xác các bạn cần nắm vững cách giải bất phương trình bậc hai một ẩn và cách tìm giao của các tập hợp số..

Vậy nên, nếu bạn chưa nắm vững được hai mảng kiến thức trên thì cần xem lại ngay trước khi đến với phần nội dung chính của bài viết này các bạn nha.

#1. Hệ bất phương trình bậc hai một ẩn có dạng như thế nào?

Hệ bất phương trình bậc hai một ẩn là một hệ các phương trình bất phương trình bậc hai có cùng một ẩn x.

Hệ bất phương trình bậc hai một ẩn có dạng $\left\{\begin{array}{c}a_1x^2+b_1x+c_1>0 \\ a_2x^2+b_2x+c_2 \geq 0 \\ a_3x^2+b_3x+c_3<0 \\ \vdots \\ a_nx^2+b_nx+c_n \leq 0 \end{array}\right.$

Trong đó:

• $a_i, b_i, c_i$ là các số thực bất kỳ.
• $a_i$ khác $0$
• $x$ là ẩn số

#2. Cách giải hệ bất phương trình bậc hai một ẩn

#3. Bài tập giải hệ bất phương trình bậc hai một ẩn

Ví dụ 1. Giải hệ bất phương trình $\left\{\begin{array}{l} x^2+9 x+7>0 \\ x^2+x-6<0 \end{array}\right.$

Lời giải:

+) Giải bất phương trình $x^2+9 x+7>0$

Đặt $f(x)=x^2+9 x+7$

Vì $a=1>0$ và $f(x)$ có hai nghiệm $x_1=\frac{-9+\sqrt{53}}{2}$, $x_2=\frac{-9-\sqrt{53}}{2}$ nên chúng ta có bảng xét dấu $f(x)$

Suy ra tập nghiệm của bất phương trình $x^2+9 x+7>0$ là $S_1=\left(-\infty, \frac{-9-\sqrt{53}}{2}\right) \cup \left(\frac{-9+\sqrt{53}}{2}, +\infty\right)$

+) Giải bất phương trình $x^2+x-6<0$

Đặt $g(x)=x^2+x-6$

Vì $a=1>0$ và $g(x)$ có hai nghiệm $x_1=-3$, $x_2=2$ nên chúng ta có bảng xét dấu $g(x)$

Suy ra tập nghiệm của bất phương trình $x^2+x-6<0$ là $S_2=(-3, 2)$

Vậy => tập nghiệm của hệ bất phương trình đã cho là $S=S_1 \cap S_2=\left(\frac{-9+\sqrt{53}}{2}, 2\right)$

Ví dụ 2. Giải hệ bất phương trình $\left\{\begin{array}{l} 4 x^2-5 x-6 \leq 0 \\ -4 x^2+12 x-5<0 \end{array}\right.$

Lời giải:

+) Giải bất phương trình $4 x^2-5 x-6 \leq 0$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Đặt $f(x)=4 x^2-5 x-6$

Vì $a=4>0$ và $f(x)$ có hai nghiệm $x_1=-\frac{3}{4}$, $x_2=2$ nên chúng ta có bảng xét dấu $f(x)$

Suy ra tập nghiệm của bất phương trình $4 x^2-5 x-6 \leq 0$ là $S_1=\left[\frac{-3}{4}, 2\right]$

+) Giải bất phương trình $-4 x^2+12 x-5<0$

Đặt $g(x)=-4 x^2+12 x-5$

Vì $a=-4<0$ và $g(x)$ có hai nghiệm $x_1=\frac{1}{2}$, $x_2=\frac{5}{2}$ nên chúng ta có bảng xét dấu $g(x)$

Suy ra tập nghiệm của bất phương trình $-4 x^2+12 x-5<0$ là $S_2=\left(-\infty, \frac{1}{2}\right) \cup \left(\frac{5}{2}, +\infty\right)$

Vậy tập nghiệm của hệ bất phương trình đã cho là $S=S_1 \cap S_2=\left[-\frac{3}{4}, \frac{1}{2}\right)$

#4. Giải nhanh bất phương trình bậc hai một ẩn bằng máy tính Casio

Đọc thêm:

Đặt mua CASIO FX-580 VNX chính hãng
Giả lập máy tính CASIO FX-580 VNX trên điện thoại, máy tính

NOTE: Ở đây mình sẽ thực hành trên máy tính cầm tay CASIO fx 580 VN X, trên các dòng máy tính cầm tay khác các bạn thực hiện tương tự

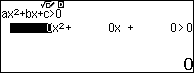
Ví dụ 3. Chẳng hạn mình cần giải bất phương trình bậc hai một ẩn $2x^2+9 x+7>0$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1. Nhấn lần lượt các phím để mở bộ giải bất phương trình bậc hai một ẩn với dấu lớn hơn.

Bước 2. Nhấn lần lượt các phím để nhập các hệ số của bất phương trình.

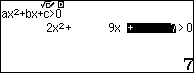
Bước 3. Nhấn phím

Vậy tập nghiệm của bất đã cho là $\left(-\infty, -\frac{7}{2}\right) \cup (-1, +\infty)$

Mặc dù CASIO FX580 VNX không hỗ trợ chúng ta giải hệ bất phương trình bậc hai một ẩn nhưng hỗ trợ giải bất phương trình bậc hai một ẩn cũng là một điều tuyệt vời rồi 🙂

#5. Lời kết

Phương pháp giải hệ bất phương trình bậc 2 một ẩn mà mình vừa trình bày không chỉ giải được hệ bất phương trình bậc hai một ẩn mà còn giải được các hệ bất phương trình bậc nhất, bậc ba, bậc bốn, … nữa nhé các bạn

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 3 cách giải phương trình bậc ba (có ví dụ dễ hiểu)
• Cách giải phương trình bậc nhất đối với sin x và cos x
• Cách giải phương trình lượng giác (có nhiều ví dụ)
• Cách giải bất phương trình tích (có ví dụ dễ hiểu)
• 3 cách giải phương trình trùng phương (có ví dụ dễ hiểu)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn