Cách giải phương trình bậc nhất đối với sin x và cos x

Xin chào tất cả các bạn !

Hôm nay, chúng ta sẽ cùng nhau tìm hiểu về cách giải phương trình bậc nhất đối với hàm số lượng giác $\sin x$ và $\cos x$

Vâng, nhằm đáp ứng nhu cầu kiểm tra và thi trắc nghiệm thì ngoài việc giải bằng phương pháp Toán học ra, mình sẽ hướng dẫn thêm thủ thuật giải nhanh bằng máy tính CASIO FX 580 VN X nữa nha các bạn.

#1. Phương trình bậc nhất đối với hàm số lượng giác sin x và cos x có dạng như thế nào?

Phương trình có dạng $a \sin x+b \cos x=c$ với $a, b$ và $c$ là những số đã cho và $a$ khác $0$ hoặc $b$ khác $0$ được gọi là phương trình bậc nhất đối với hàm số lượng giác $\sin x$ và $\cos x$

Ví dụ. $\sqrt{3} \sin x-\cos x=1$, $2 \sin 3 x+\sqrt{5} \cos 3 x=-3$ là những phương trình bậc nhất đối với hàm số lượng giác $\sin x$ và $\cos x$

#2. Phương pháp giải phương trình bậc nhất đối với hàm số lượng giác sin x và cos x

Muốn giải phương trình $a \sin x+b \cos x=c$ chúng ta thường biến đổi biểu thức $a \sin x+b \cos x$ thành biểu thức $C \sin (x+\alpha)$ hoặc $C \cos (x+\beta)$ với $C, \alpha, \beta$ là những số thực.

Dưới đây là phương pháp tổng quát giúp chúng ta biến đổi biểu thức $a \sin x+b \cos x$ thành dạng biểu thức $C \sin (x+\alpha)$

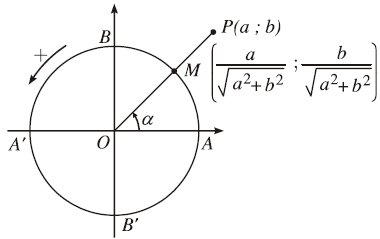
$a \sin x+b \cos x=\sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}} \sin x+\frac{b}{\sqrt{a^2+b^2}} \cos x\right)$

Vì $\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2=1$ nên điểm $M$ với tọa độ $\left(\frac{a}{\sqrt{a^2+b^2}} , \frac{b}{\sqrt{a^2+b^2}}\right)$ nằm trên đường tròn lượng giác.

Suy ra tồn tại số $\alpha$ để $\cos \alpha=\frac{a}{\sqrt{a^2+b^2}}$ và $\sin \alpha=\frac{b}{\sqrt{a^2+b^2}}$

Vậy:

$a \sin x+b \cos x$

$=\sqrt{a^2+b^2}(\cos \alpha \sin x+\sin \alpha \cos x)$

$=\sqrt{a^2+b^2} \sin (x+\alpha)$

Lúc này, thay vì phải giải phương trình lượng giác khó nhằn ($a \sin x+b \cos x=c$) thì chúng ta sẽ đi giải phương trình lượng giác cơ bản $\sin (x+\alpha)=\frac{c}{\sqrt{a^2+b^2}}$

#3. Cách phương trình bậc nhất đối với hàm số lượng giác sin x và cos x bằng máy tính Casio

Qua cách giải mình vừa trình bày ở trên thì chúng ta dễ dàng nhận thấy mấu chốt để giải được phương trình $a \sin x+b \cos x=c$ là đưa được vế trái về dạng $C \sin (x+\alpha)$, hay nói cách khác là tìm được $C$ và $\alpha$

Dưới đây là thủ thuật tìm nhanh $C$ và $\alpha$ bằng máy tính cầm tay CASIO FX 580 VN X

Để thuận tiện cho việc hướng dẫn mình sẽ chọn phương trình $\sqrt{3} \sin x-\cos x=1$

Bước 1. Nhấn lần lượt các phím  để cài đặt đơn vị góc là rađian

Bước 2. Nhấn phím  để gọi hàm Pol

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Bước 3. Nhập $a$ và $b$ vào hàm Pol

Nhấn lần lượt các phím  để nhập $Pol(\sqrt{3}, -1)$ vào máy tính cầm tay

Bước 4. Nhấn phím

Suy ra $r=C=2$

Bước 5. lần lượt nhấn các phím để tìm $\alpha$

Suy ra $\alpha=-\frac{1}{6}\pi$

Vậy $\sqrt{3} \sin x-\cos x=2 \sin \left(x-\frac{\pi}{6}\right)$

#4. Thực hành giải phương trình bậc nhất đối với hàm số lượng giác sin x và cos x

Giải phương trình $\sqrt{3} \sin x-\cos x=1$

Lời giải:

Vì:

$\sqrt{3} \sin x-\cos x$

$=2\left(\frac{\sqrt{3}}{2} \sin x-\frac{1}{2} \cos x\right)$

$=2\left(\sin x \cos \frac{\pi}{6}-\cos x \sin \frac{\pi}{6}\right)$

$=2 \sin \left(x-\frac{\pi}{6}\right)$ nên phương trình đã cho trở thành $2 \sin \left(x-\frac{\pi}{6}\right)=1$ $(*)$

$(*) \Leftrightarrow \sin \left(x-\frac{\pi}{6}\right)=\frac{1}{2}$

Vì $\sin \left(\frac{1}{2}\right)=\frac{\pi}{6}$ nên phương trình $(*)$ trở thành $\sin \left(x-\frac{\pi}{6}\right)=\sin \left(\frac{\pi}{6}\right)$ $(**)$

$(**) \Leftrightarrow\left[\begin{array} { l }  { x – \frac { \pi } { 6 } = \frac { \pi } { 6 } + k 2 \pi } \\ { x – \frac { \pi } { 6 } = \frac { 5 \pi } { 6 } + k 2 \pi } \end{array}\right.$

$(**) \Leftrightarrow \left[\begin{array}{l} x=\frac{\pi}{3}+k 2 \pi \\ x=\pi+k 2 \pi \end{array}\right.$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi}{3}+k 2 \pi$ và  $x=\pi+k 2 \pi$

#5. Lời kết

Vâng, như vậy là mình vừa hướng dẫn xong cho bạn cách giải phương trình bậc nhất đối với sin x và cos x rồi nhé.

Tuy thủ thuật sử dụng hàm Pol giúp chúng tìm ra $C$ và $\alpha$ một cách chính xác và nhanh chóng nhưng không phải lúc nào cũng tìm được.

Khi $\alpha$ là một “giá trị xấu” thì thủ thuật này sẽ không khả dụng. Và lúc bấy giờ, chúng ta phải sử dụng phương pháp biến đổi tổng quát.

Đó là đôi lời nhắc nhở mà mình muốn gởi đến các bạn trước khi tạm ngừng bút. Còn bây giờ xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nha 🙂

Đọc thêm:

• Cách giải hệ bất phương trình bậc nhất một ẩn (có ví dụ)
• Cách giải hệ bất phương trình bậc nhất hai ẩn (có ví dụ)
• 3 cách giải hệ phương trình đối xứng (có ví dụ dễ hiểu)
• 2 cách giải hệ ba phương trình bậc nhất ba ẩn, đơn giản !
• Cách giải phương trình bậc nhất đối với một hàm số lượng giác

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn