Cách giải hệ bất phương trình bậc nhất hai ẩn (có ví dụ)

Xin chào tất cả các bạn !

Trong bài viết ngày hôm nay, mình sẽ hướng dẫn các bạn cách giải hệ bất phương trình bậc nhất hai ẩn.

Có thể bạn chưa biết, hệ bất phương trình này là một trong những hệ bất phương trình quan trọng hàng đầu trong Toán học.

Nó quan trọng là bởi vì nó có nhiều ứng dụng trong thực tiễn của cuộc sống, đặc biệt là trong kinh tế.

#1. Hệ bất phương trình bậc nhất hai ẩn có dạng?

Hệ bất phương trình bậc nhất hai ẩn có dạng $\left\{\begin{array}{c}a_1x+b_1y+c_1>0 \\ a_2x+b_2y+c_2 \geq 0 \\ a_3x+b_3y+c_3<0 \\ \vdots \\ a_nx+b_ny+c_n \leq 0 \end{array}\right.$

Trong đó:

• $a_1, a_2, a_3, \dots, a_n$ là các số thực
• $b_1, b_2, b_3, \dots, b_n$ là các số thực
• $x, y$ là các ẩn

#2. Tập nghiệm của hệ bất phương trình bậc nhất hai ẩn

Trên mặt phẳng toạ độ $Oxy$, chúng ta gọi tập hợp các điểm có tọa độ thoả mãn mọi bất phương trình trong hệ là miền nghiệm của hệ.

Vậy miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

#3. Cách giải hệ bất phương trình bậc nhất hai ẩn

#4. Bài tập giải hệ bất phương trình bậc nhất hai ẩn

Giải hệ giải bất phương trình $\left\{\begin{array}{l} y-3 x>0 \\ x-2 y+5<0 \\ 5 x+2 y+10>0 \end{array}\right.$

Lời giải:

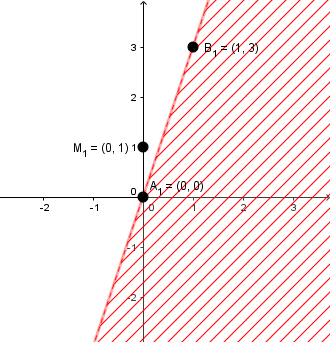
+) Giải bất phương trình $y-3 x>0$

$(d_1): y-3 x=0$ hoặc $(d_1): y=3x$

Để vẽ phương trình của đường thẳng $(d_1)$ lên mặt phẳng tọa độ $Oxy$ chúng ta cần tìm được ít nhất hai điểm thuộc $(d_1)$

Cho $x=0$ suy ra $y=0$

Cho $x=1$ suy ra $y=3$

Suy ra hai điểm thuộc đường thẳng $(d_1)$ là $A_1(0, 0)$ và $B_1(1, 3)$

Thay điểm $M_1(0, 1)$ không thuộc đường thẳng $(d_1)$ vào bất phương trình $y-3 x>0$ chúng ta được $1-3.0>0 \Leftrightarrow 1>0$

Suy ra $M_1(0, 1)$ là một nghiệm của bất phương trình $y-3 x>0$

Vậy miền nghiệm của bất phương trình $y-3 x>0$ là nữa mặt phẳng chứa điểm $M_1(0, 1)$ nhưng không bao gồm bờ của đường thẳng $(d_1)$

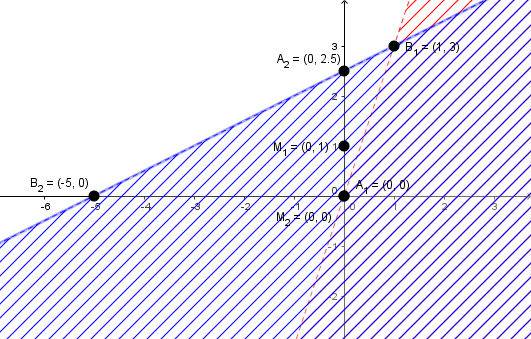
+) Giải bất phương trình $x-2 y+5<0$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

$(d_2): x-2 y+5=0$ hoặc $(d_2): y=\frac{1}{2}x+\frac{5}{2}$

Để vẽ phương trình của đường thẳng $(d_2)$ lên mặt phẳng tọa độ $Oxy$ chúng ta cần tìm được ít nhất hai điểm thuộc $(d_2)$

Cho $x=0$ suy ra $y=\frac{5}{2}$

Cho $y=0$ suy ra $x=-5$

Suy ra hai điểm thuộc đường thẳng $(d_2)$ là $A_2\left(0, \frac{5}{2}\right)$ và $B_2(-5, 0)$

Thay điểm $M_2(0, 0)$ không thuộc đường thẳng $(d_2)$ vào bất phương trình $x-2 y+5<0$ chúng ta được $0-2 .0+5<0 \Leftrightarrow 5<0$ (vô lý)

Suy ra $M_2(0, 0)$ không là một nghiệm của bất phương trình $x-2 y+5<0$

Vậy miền nghiệm của bất phương trình $x-2 y+5<0$ là nữa mặt phẳng không chứa điểm $M_2(0, 0)$ và không bao gồm bờ của đường thẳng $(d_2)$

+) Giải bất phương trình $5 x+2 y+10>0$

$(d_3): 5 x+2 y+10=0$ hoặc $(d_3): y=-\frac{5}{2}x-5$

Để vẽ phương trình của đường thẳng $(d_3)$ lên mặt phẳng tọa độ $Oxy$ chúng ta cần tìm được ít nhất hai điểm thuộc $(d_3)$

Cho $x=0$ suy ra $y=-5$

Cho $y=0$ suy ra $x=-2$

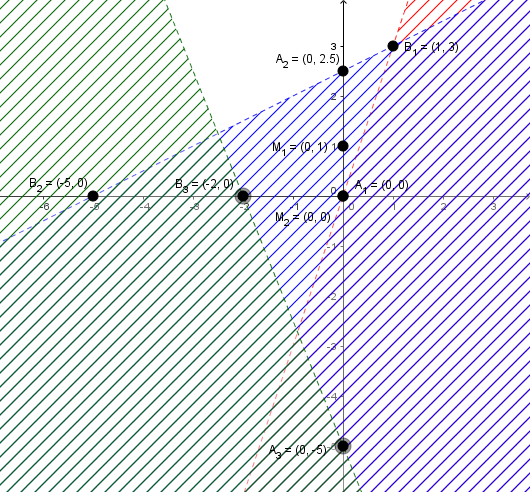
Suy ra hai điểm thuộc đường thẳng $(d_3)$ là $A_3(0, -5)$ và $B_3(-2, 0)$

Tiếp tục thay điểm $M_2(0, 0)$ không thuộc đường thẳng $(d_3)$ vào bất phương trình $5 x+2 y+10>0$ chúng ta được $5 .0+2 .0+10>0 \Leftrightarrow 10>0$

Suy ra $M_2(0, 0)$ là một nghiệm của bất phương trình $5 x+2 y+10>0$

Vậy miền nghiệm của bất phương trình $5 x+2 y+10>0$ là nữa mặt phẳng chứa điểm $M_2(0, 0)$ nhưng không bao gồm bờ của đường thẳng $(d_3)$

Vậy phần mặt phẳng không bị gạch bỏ trên mặt phẳng $Oxy$ chính là miền nghiệm của hệ bất phương trình đã cho, nhưng không kể phần biên của các đường thẳng $(d_1), (d_2), (d_3)$

Đôi lời nhận xét:

• Vì đường thẳng có vô số điểm đi qua (thuộc) nên bạn hoàn toàn có thể chọn hai điểm khác với hai điểm mà mình đã chọn.
• Điểm $M_i$ là một điểm bất kỳ trên mặt phẳng $Oxy$ miễn sao không thuộc đường thẳng đang xét.
• Nên xác định miền nghiệm của từng bất phương trình, không nên vẽ xong ba đường thẳng rồi mới xác định.

#5. Lời kết

Nếu bạn là học sinh thì bạn chỉ cần giải hệ bất phương trình bậc nhất hai ẩn là xem như xong.

Còn nếu bạn là sinh viên, hoặc giáo viên thì bạn cần phải biết thêm cách vẽ/cách minh họa miền nghiệm của hệ bất phương trình bằng máy vi tính (để soạn giáo án).

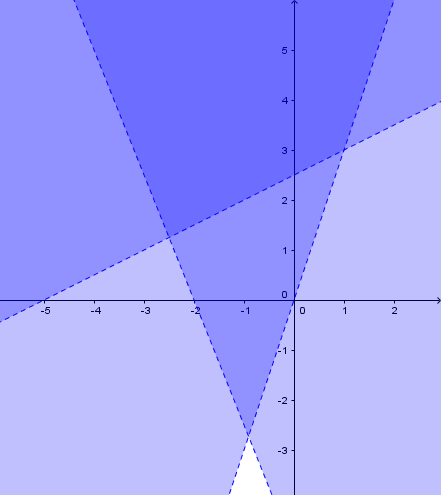
Cách thực hiện khá đơn giản, bạn chỉ cần khởi động phần mềm GeoGebra => lần lượt nhập từng bất phương trình vào thanh Input => rồi nhấn phím Enter là xong (mỗi lần chỉ nhập một bất phương trình).

Phần mặt phẳng được tô màu đậm nhất chính là tập nghiệm của hệ bất phương trình đã cho.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách giải hệ bất phương trình bậc nhất một ẩn (có ví dụ)
• 2 cách giải bất phương trình bậc nhất một ẩn (có ví dụ)
• Cách giải bất phương trình bậc nhất hai ẩn (có VÍ DỤ)
• 2 cách giải hệ ba phương trình bậc nhất ba ẩn, đơn giản !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn