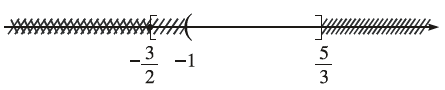Cách giải hệ bất phương trình bậc nhất một ẩn (có ví dụ)

Hôm nay, chúng ta sẽ cùng nhau tìm hiểu về cách giải hệ bất phương trình bậc nhất một ẩn nha các bạn.

Đầu tiên, mình sẽ trình bày về khái niệm, tiếp theo sẽ là cách giải và cuối cùng là vận dụng những kiến thức vừa trình bày để thực hành giải hệ bất phương trình bậc nhất một ẩn.

Xem thêm:

• Cách tìm giao của hai tập hợp
• Cách giải bất phương trình bậc nhất một ẩn

#1. Hệ bất phương trình bậc nhất một ẩn là gì?

Hệ bất phương trình bậc nhất một ẩn có dạng $\left\{\begin{array}{} a_1x+b_1>0 \\ a_2x+b_2 \geq 0 \\ a_3x+b_3<0 \\ \vdots \\ a_nx+b_n \leq 0 \end{array}\right.$, với:

• $a_1, a_2, a_3, …, a_n$ là các số thực khác không
• $b_1, b_2, b_3, …, b_n$ là các số thực bất kỳ
• $x$ là ẩn

Dễ thấy $\left\{\begin{array}{l} 6 x-10 \leq 0 \\ 6 x+9 \geq 0 \\ 4x+4>0 \end{array}\right.$ hoặc $\left\{\begin{array}{l} 25 x-10>20 x+25 \\ 30 x-24<6x+12 \end{array}\right.$ là những hệ bất phương trình bậc nhất một ẩn.

#2. Cách giải hệ bất phương trình bậc nhất một ẩn

Như các bạn đã biết thì tập nghiệm của hệ phương trình là tập giao của tất cả các tập nghiệm của các phương trình trong hệ.

Một cách tương tự, chúng ta cũng có tập nghiệm của hệ bất phương trình bậc nhất một ẩn là giao của tất cả các tập nghiệm của các bất phương trình trong hệ.

Vậy muốn giải hệ bất phương trình một ẩn chúng ta giải từng bất phương trình trong hệ rồi lấy giao của các tập nghiệm vừa tìm được.

#3. Cách giải hệ bất phương trình bậc nhất một ẩn

Ví dụ 1. Giải hệ bất phương trình $\left\{\begin{array}{l} 6 x-10 \leq 0 \\ 6 x+9 \geq 0 \\ 4x+4>0 \end{array}\right.$

Lời giải:

Lần lượt giải các bất phương trình bậc nhất $6 x-10 \leq 0$ và $2 x+3 \geq 0$ và $4x+4>0$

$6 x-10 \leq 0 \Leftrightarrow 3 x-5 \leq 0 \Leftrightarrow 3x \leq 5 \Leftrightarrow x \leq \frac{5}{3}$

=> Tập nghiệm của bất phương trình là $S_1=\left(-\infty ; \frac{5}{3}\right]$

$6 x+9 \geq 0 \Leftrightarrow 2 x+3 \geq 0 \Leftrightarrow 2x \geq -3 \Leftrightarrow x \geq -\frac{3}{2}$

=> Tập nghiệm của bất phương trình là $S_2=\left[-\frac{3}{2} ;+\infty\right)$

$4x+4>0 \Leftrightarrow x+1 > 0 \Leftrightarrow x>-1$

=> Tập nghiệm của bất phương trình là $S_3=(-1 ;+\infty)$

Giao của các tập nghiệm của các bất phương trình vừa tìm được là $S=S_1 \cap S_2 \cap S_3=\left(-1 ; \frac{5}{3}\right]$

Vậy tập nghiệm của hệ bất phương trình đã cho là $\left(-1 ; \frac{5}{3}\right]$

Xem thêm:
Cách vẽ trục số, biểu diễn tập hợp trên trục số bằng GeoGebra

Ví dụ 2. Giải hệ bất phương trình $\left\{\begin{array}{l} 25 x-10>20 x+25 \\ 30 x-24<6x+12 \end{array}\right.$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Lời giải:

Lần lượt giải các bất phương trình bậc nhất $25 x-10>20 x+25$ và $30 x-24<6x+12$

$25 x-10>20 x+25 \Leftrightarrow 5 x-2>4 x+5 \Leftrightarrow x > 7$

=> Tập nghiệm của bất phương trình là $S_1=\left(7, +\infty\right)$

$30 x-24<6x+12 \Leftrightarrow 5 x-4<x+2 \Leftrightarrow x< \frac{3}{2}$

=> Tập nghiệm của bất phương trình là $S_2=\left(-\infty, \frac{3}{2}\right)$

Giao của các tập nghiệm của các bất phương trình vừa tìm được là $S=S_1 \cap S_2=\varnothing$

Vậy => tập nghiệm của hệ bất phương trình đã cho là $\varnothing$ hoặc hệ bất phương trình đã cho vô nghiệm.

#4. Lời kết

Mục đích của việc giải hệ bất phương trình bậc nhất một ẩn là để rèn luyện lại kỹ năng giải bất phương trình bậc nhất một ẩn và cách tìm giao của các tập hợp số.

Ngoài ra, việc giải hệ bất phương trình này còn giúp các bạn dễ dàng tiếp cận với cách giải hệ bất phương trình bậc nhất hai ẩn

Okay, hi vọng những thông tin trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn