Các tìm giao, tìm hợp, phần bù và hiệu của hai tập hợp

Xin chào tất cả các bạn !

Hôm nay, mình sẽ hướng dẫn các bạn thực hiện các phép toán như (hợp, giao, phần bù và hiệu) với hai tập hợp bất kỳ.

Việc tìm được hợp, giao, phần bù và hiệu của hai tập hợp có nhiều ứng dụng trong Toán học.

Dễ thấy nhất là khi giải hệ bất phương trình bậc nhất một ẩn, hệ bất phương trình bậc hai một ẩn, hệ bất phương trình bậc nhất hai ẩn,…

#1. Tập hợp

Tập hợp là một trong những khái niệm nguyên thủy của Toán học nên rất khó để  định nghĩa.

Thông thường, mỗi tập hợp sẽ bao gồm các phần tử cùng có chung một hay một vài tính chất nào đó.

Chúng ta thường cho tập hợp bằng một trong ba cách bên dưới:

1. Liệt kê các phần tử của tập hợp.
2. Chỉ rõ các tính chất đặc trưng cho các phần tử của tập hợp.
3. Biểu đồ Ven.

Tập hợp không chứa phần tử nào được gọi là tập rỗng và được kí hiệu là $\varnothing$

Bạn có thể xem định nghĩa về tập hợp cũng như định nghĩa về tập hơn con trong bài viết này:

• Tập hợp là gì? tập hợp con là gì? Hai tập hợp bằng nhau?

#2. Tên gọi, kí hiệu và biểu diễn của một số tập hợp thường gặp

Tên gọi và kí hiệu	Tập hợp	Biểu diễn trên trục số (phần không bị gạch chéo)
Tập số thực $(-\infty;+\infty)$	$\mathbb{R}$
Đoạn $[a;b]$	${x\in\mathbb{R}\mid a\le x\le b}$
Khoảng $(a;b)$	${x\in\mathbb{R}\mid a<x<b}$
Nửa khoảng $[a;b)$	${x\in\mathbb{R}\mid a\le x<b}$
Nửa khoảng $(a;b]$	${x\in\mathbb{R}\mid a<x\le b}$
Nửa khoảng $(-\infty;a]$	${x\in\mathbb{R}\mid x\le a}$
Nửa khoảng $[a;+\infty)$	${x\in\mathbb{R}\mid x\geq a}$
Khoảng $(-\infty;a)$	${x\in\mathbb{R}\mid x<a}$
Khoảng $(a;+\infty)$	${x\in\mathbb{R}\mid x>a}$

Ý nghĩa của các kí hiệu mà mình vừa trình bày:

• $-\infty$ đọc là âm vô cực.
• $+\infty$ đọc là dương vô cực.
• $a$ và $b$ được gọi là các đầu mút của đoạn hoặc khoảng hoặc nửa khoảng.

#3. Cách tìm hợp của hai tập hợp

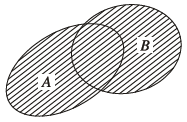
Hợp của hai tập $A$ và $B$ là tập bao gồm tất cả các phần tử thuộc $A$ hoặc thuộc $B$.

Lúc này, chúng ta ký hiệu là $A \cup B$

Diễn đạt bằng ký hiệu Toán học thuần túy là $A \cup B=\{x \mid x \in A$ hoặc  $x \in B\}$

Phần gạch chéo biểu diễn hợp của hai tập $A$ và $B$

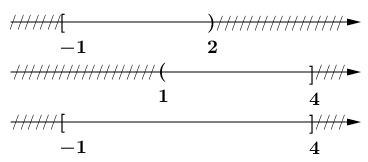
Ví dụ 1. Cho nửa khoảng $A=[-1 ; 2)$ và nửa khoảng $B=(1 ; 4]$

Tìm $A \cup B$

Lời giải:

Để xác định chính xác và nhanh chóng $A \cup B$ chúng ta sẽ biểu diễn hai tập hợp đã cho trên trục số.

=> $A \cup B=[-1 ; 4]$

#4. Cách tìm giao của tập hợp

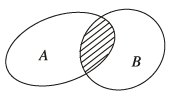
Giao của hai tập $A$ và $B$ là tập bao gồm tất cả các phần tử thuộc cả $A$ và $B$

Lúc này, chúng ta ký hiệu là $A \cap B$

Diễn đạt bằng ký hiệu Toán học thuần túy là $A \cap B=\{x \mid x \in A$ và $x \in B\}$

Nếu hai tập $A$ và $B$ không có phần tử chung nghĩa là $A \cap B=\varnothing$ thì chúng ta gọi $A$ và $B$ là hai tập rời nhau

Phần gạch chéo biểu diễn giao của hai tập $A$ và $B$

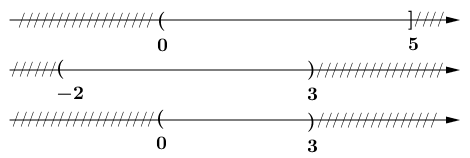
Ví dụ 2. Cho nửa khoảng $A=(0 ; 5]$ và khoảng $B=(-2 ; 3)$

Tìm $A \cap B$

Lời giải:

Để xác định chính xác và nhanh chóng $A \cap B$ chúng ta sẽ biểu diễn hai tập hợp đã cho trên trục số.

Suy ra $A \cap B=(0 ; 3)$

#5. Cách tìm phần bù của hai tập hợp

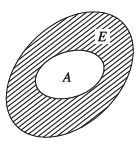
Cho $A$ là tập con của tập $E$

Phần bù của $A$ trong $E$ là tập tất cả các phần tử của $E$ mà không là phân tử của $A$

Lúc này chúng ta ký hiệu $\mathrm{C}_E A$

Phần gạch chéo biểu diễn phần bù của tập $A$ trong $E$

#6. Cách tìm hiệu của hai tập hợp

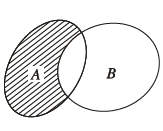
Hiệu của hai tập $A$ và $B$ là tập bao gồm tất cả các phần tử thuộc $A$ nhưng không thuộc $B$

Lúc này chúng ta ký hiệu là $A \backslash B$

Diễn đạt bằng ký hiệu Toán học thuần túy là  $A \backslash B=\{x \mid x \in A$ và $x \notin B\}$

Phần gạch chéo biểu diễn hiệu của hai tập $A$ và $B$

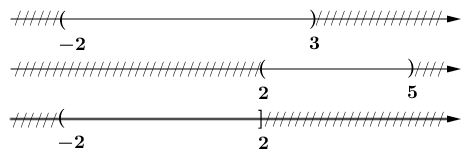
Ví dụ 3. Cho khoảng $A=(-2 ; 3)$ và khoảng $B=(2 ; 5)$. Tìm $A \backslash B$

Lời giải:

Để xác định chính xác và nhanh chóng $A \backslash B$ chúng ta sẽ biểu diễn hai tập hợp đã cho trên trục số.

=> $A \backslash B=(-2 ; 2]$

#7. Lời kết

Có thể nói, việc tìm hợp của hai tập hợp, tìm giao của hai tập hơn, phần bù của hai tập hợp và hiệu của hai tập hợp không có gì khó khăn phức tạp cả.

Tuy nhiên, nếu bạn chưa quen thì nên biểu diễn các tập hợp đã cho trên trục số trước để tránh những sai sót không đáng có trong quá trình làm bài tập.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn