Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Xin chào tất cả các bạn !
Hôm nay mình sẽ lần lượt trình bày tất cả các kiến thức cơ bản có liên quan đến tập hợp như: khái niệm về tập hợp, số phần tử của tập hợp, tập hợp con, hai tập hợp bằng nhau và giao của hai tập hợp..
Và từ những kiến thức trên bạn có thể hiểu và hình dung được thế nào là một tập hợp, biết cách sử dụng kí hiệu $\in$ và $\notin$, biết cách xác định một tập hợp, …
Ngay bây giờ chúng ta hãy cùng nhau bắt đầu nhé…
Mục Lục Nội Dung
#1. Tập hợp là gì?
Theo Wikipedia thì Tập hợp là một bộ các phần tử.
Các phần tử tạo nên một tập hợp có thể là bất kỳ loại đối tượng toán học nào: Ví dụ như số, ký hiệu, điểm trong không gian, đường thẳng, hay các hình dạng hình học khác, các biến hoặc thậm chí là các tập hợp khác.
Nói chung, tập hợp là một khái niệm nguyên thủy nên rất khó để định nghĩa. Vì vậy chúng ta có thể hình dung nó thông qua các ví dụ.
- Tập hợp các số tự nhiên có một chữ số.
- Tập hợp các học sinh của lớp 6/1
- Tập hợp các giáo viên của Trường THCS Đại Hòa Lộc
Người ta thường sử dụng các chữ cái in hoa A, B, C, …, X, Y, Z để đặt tên cho các tập hợp.
Phần tử của một tập hợp là cá thể tạo nên tập hợp đó.
Ví dụ.
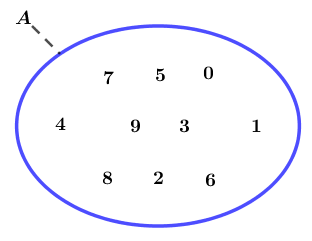
Cho tập hợp $A=\{0; 1; 2; 3; 4; 5; 6; 7; 8; 9\}$, mỗi chữ số trong A được gọi là một phần tử.
- Số 0 là một phần tử của tập hợp A, lúc bấy giờ ta nói 0 thuộc A, kí hiệu $0 \in A$
- Số 10 không là một phần tử của tập hợp A, lúc bấy giờ ta nói 10 không thuộc A, kí hiệu $10 \notin A$
Người ta thường xác định một tập hợp bằng một trong ba cách sau:
- Cách 1. Liệt kê các phần tử của tập hợp (mỗi phần tử chỉ được liệt kê một lần và không kể đến thứ tự).
- Cách 2. Chỉ ra các tính chất đặc trưng của các phần tử trong tập hợp.
- Cách 3. Sử dụng sơ đồ Venn (sơ đồ Venn là một vòng kín, bên trong có các chấm chỉ các phần tử của nó, tên tập hợp được viết ở biên).
Áp dụng vào ví dụ ta được:
Cách 1: $A=\{0; 1; 2; 3; 4; 5; 6; 7; 8; 9\}$
Cách 2: $A=\{x \in N | x < 10\}$
Cách 3:
#2. Số phần tử của một tập hợp?
Một tập hợp có thể có một phần tử, hai phần tử, ba phần tử, hoặc n phần tử… Tập hợp không có phần tử nào gọi là tập hợp rỗng và được kí hiệu là $\emptyset$
Nếu số phần tử của tập hợp không thể đếm được thì tập hợp đó có vô số phần tử. Tập hợp các số tự nhiên là một tập hợp có vô số các phần tử.
Chú ý: Tập hợp $\{0\}$ không phải là tập hợp rỗng vì nó có một phần tử là số 0
#3. Tập hợp con là gì?
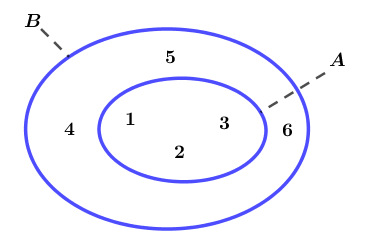
Cho tập hợp $A=\{1; 2; 3\}$ và $B=\{1; 2; 3; 4; 5; 6\}$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Dễ thấy mỗi phần tử của A là một phần tử của B. Lúc bấy giờ ta nói A là tập hợp con của tập hợp B, kí hiệu là $A \subset B$
Ngoài ra, người ta còn nói B chứa A, hoặc A được chứa trong B, kí hiệu là $B \supset A$
Chú ý:
- Tập hợp rỗng là con của một tập hợp bất kỳ, $\emptyset \subset A$
- Một tập hợp bất kỳ là con của chính nó, $A \subset A$
#4. Hai tập hợp bằng nhau khi nào?
Tập hợp A bằng tập hợp B khi và chỉ khi mỗi phần tử của A là một phần tử của B và ngược lại, mỗi phần tử của B là một phần tử của A.
Kí hiệu là $A=B$
Chúng ta cũng có thể trình bày định nghĩa bằng ký hiệu Toán học thuần túy như này:
$A=B \Leftrightarrow \left\{\begin{array}{ll}A \subset B \\ B \subset A \end{array}\right.$
Cho tập hợp $A=\{1, 2, 3, 4, 5, 6\}$ và $B=\{x \in N^* | x < 7\}$, theo định nghĩa trên dễ thấy $A=B$
#5. Giao của hai tập hợp là gì?
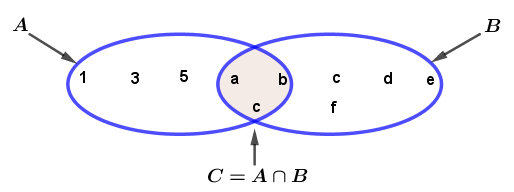
Cho tập hợp $A=\{1; a; 3; b; 5; c\}$, $B=\{a; b; c; d; e; f\}$ và $C=\{a; b; c\}$
Dễ thấy, tập hợp C gồm các phần tử vừa thuộc A vừa thuộc B. Vậy => C là tập hợp giao của A và B, kí hiệu $C=A \cap B$
#6. Lời kết
Vâng, trên đây là toàn bộ những kiến thức liên quan đến tập hợp, tập hợp con mà bạn cần phải biết.
Các kiến thức mà mình vừa giới thiệu đều là những kiến thức rất cơ bản, vì vậy mình tin rằng các bạn có thể nắm được một cách dễ dàng thôi.
Nếu có thời gian bạn có thể tìm hiểu thêm về các phép toán khác trên tập hợp như phép hợp, phép hiệu, phần bù đại số, … để nâng cao kiến thức ha.
Chúc các bạn học tập tốt. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Các tính chất của phép chia hết (kí hiệu, cách áp dụng..)
- 4 tính chất của phép cộng và phép nhân các số tự nhiên
- {Tips & Tricks} Các dấu hiệu chia hết cho 2, 3, 4, 5, 6, 7, 8, 9
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
