Các tính chất của phép chia hết (kí hiệu, cách áp dụng..)

Vâng, qua bài viết này thì các bạn sẽ nắm được các tính chất chia hết của tổng và của hiệu.

Và bạn cũng sẽ biết cách nhận biết được một tổng của hai hay nhiều số, hay một hiệu của hai hay nhiều số có chia hết hay không chia hết cho một số mà không cần tính giá trị của tổng hoặc của hiệu tương ứng.

#1. Phép chia hết là gì?

Phép chia hết là phép chia có số dư bằng 0. Hiểu đơn giản vậy thôi !

Cho hai số tự nhiên a và b, với $b \neq 0$ nếu tồn tại số tự nhiên k sao cho $a=bk$ thì ta nói a chia hết cho b.

Ví dụ:

• 6 chia hết cho 3 vì $6=3.2$
• 6 không chia hết cho 4 vì không tồn tại bất kì số tự nhiên k nào để biểu thức $6=4k$ xảy ra cả.

Kí hiệu $a \vdots b$ ý nói a chia hết cho b và ngược lại a  b ý nói a không chia hết cho b.

#2. Tính chất của phép chia hết

Nếu tất cả các số hạng của một tổng cùng chia hết cho một số khác 0 thì tổng của chúng chia hết cho số đó.

$a \vdots m, b \vdots m \Rightarrow a+b \vdots m$

$2 \vdots 2, 4 \vdots 2 \Rightarrow 2+4 \vdots 2$

Ở đây mình chỉ chứng minh cho trường hợp hai số hạng của một tổng, các trường hợp còn lại các bạn chứng minh hoàn toàn tương tự ha.

Chứng minh $a \vdots m, b \vdots m \Rightarrow a+b \vdots m$

• Vì $a \vdots m$ nên tồn tại số tự nhiên a’ sao cho $a=ma’$
• Vì $b \vdots m$ nên tồn tại số tự nhiên b’ sao cho $b=mb’$

Ta có $a+b=ma’+mb’=m(a’+b’)$, mặc khác ta lại có $a’+b’ \in N$

Vậy => $a+b$ chia hết cho m.

Nếu số bị trừ và số trừ cùng chia hết cho một số khác 0 thì hiệu của chúng chia hết cho số đó.

$a \geq b, a \vdots m, b \vdots m \Rightarrow a-b \vdots m$

Trong một tổng, chỉ cần có một số hạng không chia hết cho một số, cho dù các số hạng còn lại chia hết cho số đó thì tổng vẫn không chia hết cho số đó.

$a \vdots m$, $b$ $m \Rightarrow a+b$  $m$

$12 \vdots 4$,  $7$ $4 \Rightarrow 12-7$  $4$

Chứng minh:

• Vì $a \vdots m$ nên tồn tại số tự nhiên $a’$ sao cho $a=ma’$
• Vì $b$ $m$ nên tồn tại các số tự nhiên $b’$ và $r$ sao cho $b=mb’+r, (0<r<m)$

Ta có $a+b=ma’+mb’+r=m(a’+b’)+r$, mặc khác ta lại có $a’+b’ \in N$ và $0 < r < m$ nên $a+b$ không chia hết cho $m$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Nếu số bị trừ chia hết cho một số, nhưng số trừ không chia hết cho số đó hoặc ngược lại số bị trừ không chia hết cho số đó, nhưng số trừ chia hết cho số đó thì hiệu không chia hết cho số đó.

• $a \geq b, a \vdots m$, $b$ $m \Rightarrow a-b$  $m$
• $a \geq b$, $a$ $m$, $b \vdots m \Rightarrow a-b$  $m$

#3. Một số điểm cần lưu ý về phép chia hết

Trong quá trình giải toán có thể chúng ta sẽ gặp trường hợp $a$  $m$, $b$  $m$ nhưng $a+b \vdots m$

$3$  $2$, $5$ $2$ nhưng $3+5 \vdots 2$

Tương tư như trên ta cũng có thể gặp trường hợp $a$  $m$, $b$  $m$ nhưng $a-b \vdots m$

$25$ $4$, $13$ $4$ nhưng $25-13 \vdots 4$

#4. Cách viết a+b và (a+b)

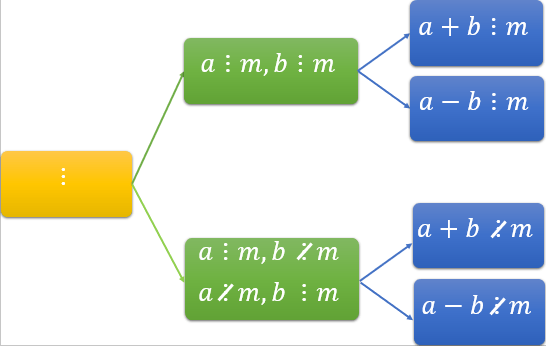
#5. Sơ đồ hệ thống kiến thức về phép chia hết

Dưới đây là sơ đồ hệ thống các trường hợp cơ bản, thường gặp khi giải các bài toán chia hết.

#6. Lời kết

Okay, như vậy là thông qua bài viết này thì bạn đã hiểu được rõ hơn về tính chất của phép chia hết rồi phải không.

Trong thực tế, khi giải các bài toán chia hết chúng ta thường gặp trường hợp một tổng mà trong đó có đúng hai số hạng không chia hết cho m

Lúc bấy giờ, muốn xét xem tổng này có chia hết cho m hay không thì ta thường gộp hai số hạng đó với nhau, hoặc gộp hai số dư trong phép chia cho m của hai số đó với nhau.

Ví dụ, xét xem biểu thức $A=612+240+17+22$ có chia hết cho 6 hay không:

$A=612+240+(17+22)=612+240+39$ => Dễ thấy A không chia hết cho 6 đúng không nào.

Okay, hi vọng là bài viết này sẽ giúp ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 2 cách tìm BỘI CHUNG và BỘI CHUNG NHỎ NHẤT (rất dễ)
• 3 cách tìm ƯỚC CHUNG và ƯỚC CHUNG LỚN NHẤT (rất dễ)
• {Tips & Tricks} Các dấu hiệu chia hết cho 2, 3, 4, 5, 6, 7, 8, 9

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com