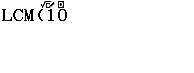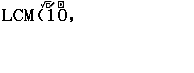2 cách tìm BỘI CHUNG và BỘI CHUNG NHỎ NHẤT (rất dễ)

Qua bài viết này các bạn cần nắm được định nghĩa về bội chung và định nghĩa về bội chung nhỏ nhất của hai hay nhiều số, cũng như biết cách tìm …

• Tìm bội chung bằng phương pháp liệt kê.
• Tìm bội chung nhỏ nhất bằng Phương pháp 1 (Phân tích ra thừa số nguyên tố).
• Tìm bội chung thông qua bội chung nhỏ nhất.

Ngoài ra bạn cũng cần ghi nhớ mối quan hệ giữa tích hai số, ước chung lớn nhất, bội chung nhỏ nhất

I. Bội chung là gì?

• Đọc thêm: Bội số là gì?

#1. Định nghĩa

Số tự nhiên x là bội của số tự nhiên a và cũng là bội của số tự nhiên b thì ta nói, x là bội chung của a và b.

“Bội” chính là số bị chia.

$BC(a,b)=\{x \in N|x \vdots a, x \vdots b\}$

Hay nói một cách tổng quát ta có bội chung của hai hay nhiều số là bội chung của tất cả các số đó.

#2. Các bước tìm bội chung của 2 số a và b

Ví dụ: Tìm bội chung của 22, 46

Bước 1. Tìm bội của số 22

$B(22)=\{22,44,66,…,462,484,506…\}$

Bước 2. Tìm bội của số 46

$B(46)=\{46,92,138,…,414,460,506,…\}$

Bước 3. Tìm giao của $B(22)$ và $B(46)$

$BC(22,46)=B(22) \cap B(46)=\{506,1012, 1518, …\}$

II. Bội chung nhỏ nhất là gì?

#1. Định nghĩa

Bội chung nhỏ nhất (BCNN)  của hai hay nhiều số là số nhỏ nhất {khác 0} trong tập hợp các bội chung của các số đó.

Hay nói cách khác: Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất trong tập hợp các bội chung của chúng.

Bội chung nhỏ nhất của hai số tự nhiên a và b là số nhỏ nhất trong tập hợp các bội chung của chúng.

$BCNN(a,b)$ hoặc $[a,b]$ nếu không có sự nhầm lẫn.

#2. Các bước tìm bội chung nhỏ nhất của hai số a, b

Về cơ bản có hai phương pháp để tìm bội chung nhỏ nhất của hai số tự nhiên a và b

Ví dụ. Tìm bội chung nhỏ nhất của 10 và 12

Bước 1. Phân tích 10, 12 ra thừa số nguyên tố.

$10=2.5$

$12=2^2.3$

Bước 2. Chọn ra các thừa số nguyên tố chung và riêng.

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

$2, 5, 3$

Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất.

$2^2.3.5=60$

Vậy => $BCNN(10,12)=60$

#3. Mối quan hệ giữa bội, bội chung, bội chung nhỏ nhất của hai số a và b

Mối quan hệ của bội, bội chung, bội chung nhỏ nhất của hai số a, b được thể hiện bởi biểu thức $BC(a,b)=B(BCNN(a,b))$

Chúng ta có thể ứng dụng mối quan hệ này để tìm nhanh bội chung của hai số a, b

Ví dụ. Tìm bội chung của 2022, 30

$BCNN(2022,30)=10110$

$BC(2022,30)=B(10110)=\{10110,20220,30330,…\}$

III. Mối quan hệ giữa tích hai số, ước chung lớn nhất, bội chung nhỏ nhất

Khi biết tích của hai số và ước chung lớn nhất (UCLN) hoặc bội chung nhỏ nhất (BCNN) thì ta sẽ dễ dàng tìm được bội chung nhỏ nhất hoặc ước chung lớn nhất tương ứng.

Tính chất trên được suy ra từ biểu thức $a.b=UCLN(a,b).BCNN(a,b)$

IV. Lời kết

Vâng, trên đây là 2 cách tìm bội chung và bội chung nhỏ nhất đơn giản nhất. Và cũng tương tự như bài viết trước, qua bài viết này mình cũng xin rút ra một số kinh nghiệm nhỏ gửi đến các bạn như sau:

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 7 cách giải phương trình bậc hai đơn giản, hiệu quả
• 2 cách tìm ƯỚC SỐ và BỘI SỐ (sử dụng công thức & Casio fx)
• Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng CASIO

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com