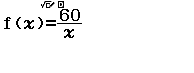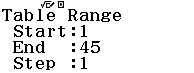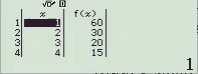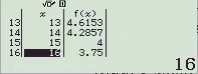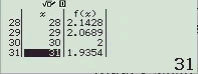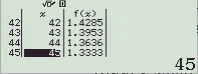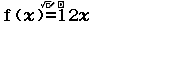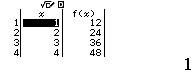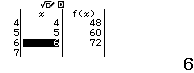2 cách tìm ƯỚC SỐ và BỘI SỐ (sử dụng công thức & Casio fx)

Qua bài viết này các bạn cần phải:

• Nêu được định nghĩa của ƯỚC SỐ và BỘI SỐ của một số tự nhiên, biết viết tập hợp các ước, các bội.
• Biết cách kiểm tra một số tự nhiên cho trước có là ước hoặc là bội của một số tự nhiên cho trước hay không.
• Tìm được ước và bội trong những trường hợp đơn giản (số nhỏ).

I. ƯỚC SỐ và BỘI SỐ là gì?

Cho hai số tự nhiên a và b. Nếu a chia hết cho b thì chúng ta nói b là ước của a hoặc a là bội của b. Đơn giản vậy thôi !

Có thể hiểu: BỘI là số bị chia.

• Tập hợp tất cả các ước của một số a được kí hiệu là U(a)
• Tập hợp tất cả các bội của một số a được kí hiệu là B(a)

Ví dụ:

$U(8)={1, 2, 4, 8}$

$B(9)=\{9, 18, 27, 36, 45, 54, …\}$

II. Cách viết tập hợp ƯỚC và BỘI trong trường hợp tổng quát

• Tập hợp các ước của a là $U(a)=\{x \in N^* | a \vdots x\}$
• Tập hợp các bội của b là $B(b)=\{x \in N | x \vdots b\}$ hoặc $B(b)=\{b.n | n \in N\}$ hoặc $B(b)=\{0, b, 2b, 3b, 4b, …\}$

III. Các bước tìm ước của một số tự nhiên

Giả sử chúng ta cần tìm tất cả các Ước số của a

#1. Phương pháp Toán học

#2. Phương pháp sử dụng máy tính CASIO fx-580VN X

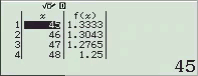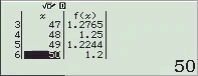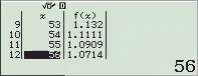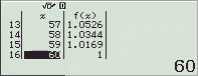
Ví dụ: Tìm tất cả các ước của 60

Cách 1: Sử dụng phương phép Toán học

60 chia hết cho 1, 2, 3, 4, 5, 6, 12, 15, 20, 30, 60

=> Vậy $U(60)=\{1, 2, 3, 4, 5, 6, 12, 15, 20, 30, 60\}$

Cách 2: Sử dụng phương pháp sử dụng máy tính CASIO fx-580VN X

Bước 1. Thiết lập chỉ sử dụng duy nhất một hàm f(x)

Bước 2. Chọn phương thức tính toán Table

Bước 3. Nhập hàm f(x)

Bước 4. Nhập Start = 1, End = 45, Step = 1

Bước 5. Nhấn phím =

Bước 5 plus. Nhập Start = 45, End = 60, Step = 1

NOTE: Như mình có note ở bên trên, do a > 45 nên ta phải thực hiện bước này lần nữa.

=> Vậy $U(60)=\{1, 2, 3, 4, 5, 6, 12, 15, 20, 30, 60\}$

IV. Các bước tìm bội của một số tự nhiên

Giả sử chúng ta cần tìm các bội của a

#1. Phương pháp Toán học

Để tìm các bội của một số tự nhiên a chúng ta sẽ lần lượt nhân a với 1, 2, 3, …

#2. Phương pháp sử dụng máy tính CASIO fx-580VN X

Bước 1. Thiết lập chỉ sử dụng duy nhất một hàm f(x)

Bước 2. Chọn phương thức tính toán Table

Bước 3. Nhập hàm $f(x)=ax$

Bước 4. Nhập Start =1, End=Số lượng bội cần tìm, Step = 1

Do giới hạn về khả năng tạo bảng chúng ta chỉ có thể tạo được tối đa 45 giá trị trên một lần

Nói như vậy có nghĩa là nếu số lượng bội cần tìm lớn hơn 45 thì bạn cần thực hiện nhiều lần, bao nhiêu lần phụ thuộc vào số lượng bội cần tìm, số lượng càng lớn thì số lần thực hiện các nhiều

Bước 5. Nhấn phím =

Ví dụ: Tìm sáu bội đầu tiên của 12

Sử dụng phương pháp Toán học

$12.1=12, 12.2=24, 12.3=36, 12.4=48, 12.5=60, 12.6=72$

Vậy $B(12)=\{12, 24, 36, 48, 60, 72\}$

Sử dụng phương pháp sử dụng máy tính CASIO fx-580VN X

Bước 1. Thiết lập chỉ sử dụng duy nhất một hàm f(x)

Bước 2. Chọn phương thức tính toán Table

Bước 3. Nhập hàm $f(x)=12x$

Bước 4. Nhập Start =1, End=6, Step = 1

Bước 5. Nhấn phím =

Vậy $B(12)=\{12, 24, 36, 48, 60, 72\}$

V. Một số chú ý về Ước số và Bội số

• Tập hợp ước của một số tự nhiên là tập hợp hữu hạn.
• Tập hợp bội của một số tự nhiên là vô hạn.
• Số 1 là ước của mọi số tự nhiên.
• Số tự nhiên khác 0 là ước của chính nó.
• Số 0 là bội của mọi số tự nhiên.
• Không tồn tại bất kì số nào là ước của số 0

VI. Lời kết

Như vậy các bạn có thể thấy: việc tìm bội số của một số tự nhiên bất kỳ không có gì khó khăn, nhưng việc tìm ước thì lại khác, không phải lúc nào chúng ta cũng dễ dàng tìm. Đặc biệt là khi số cần tìm có giá trị lớn.

Nếu làm theo một trong hai cách mà mình vừa trình bày thì tốn khá nhiều thời gian và công sức. Vậy nên vấn đề này sẽ được giải quyết trong bài phân tích một số ra thừa số nguyên tố, các bạn nhớ tìm đọc trên blog nhé.

Hi vọng là bào viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

• Đọc thêm: 3 cách tìm ƯỚC CHUNG và ƯỚC CHUNG LỚN NHẤT (rất dễ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com