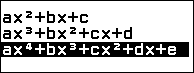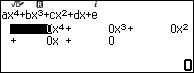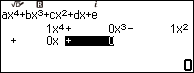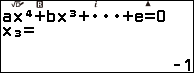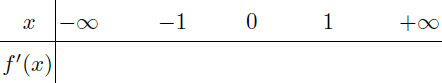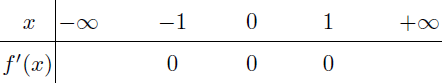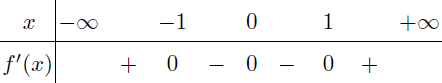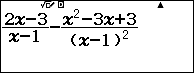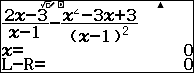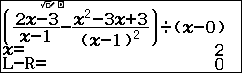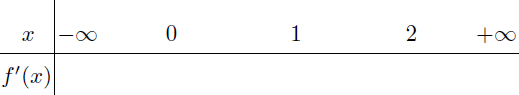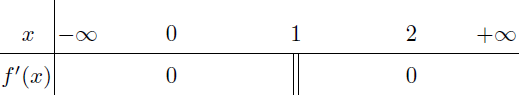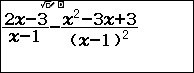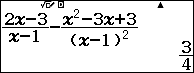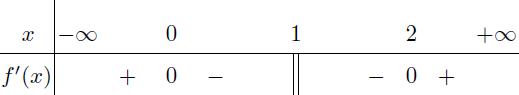Sử dụng máy tính Caiso fx 580 VNX hoặc Fx 880 BTG
Chào các bạn, trong bài viết này mình sẽ hướng dẫn các bạn cách sử dụng máy tính CASIO để xét sự biến thiên (đồng biến, nghịch biến) của một hàm số bất kì.
Thủ thuật mà mình lựa chọn mặc dù dài hơn các thủ thuật khác nhưng dễ hiểu hơn và sử dụng được cho cả trắc nghiệm và tự luận.
Để thực hiện được thủ thuật này thì các bạn cần sử dụng thành thạo tính năng giải phương trình đa thức Equation (Polynomial), tính năng tìm nghiệm của phương trình bất kì Solver, tính năng CALC, …
Mục Lục Nội Dung
#1. Các bước thực hiện
Các bước sử dụng máy tính CASIO hỗ trợ xét sự biến thiên của hàm số f(x) bất kì như sau:
Bước 1. Tìm tập xác định của hàm số.
Bước này bạn có thể sử dụng tính năng giải phương trình đa thức Equation (Polynomial), và tính năng tìm nghiệm của phương trình bất kì Solver để hỗ trợ.
Bước 2. Sử dụng kiến thức Toán học để tìm f’(x)
Bước 3. Tìm các nghiệm $x_i$ (i=1, 2, 3, …) của phương trình f’(x)=0
Để tìm các nghiệm $x_i$ bạn có thể sử dụng tính năng Equation (Polynomial) hoặc tính năng Solver / SOLVE
- Nếu f’(x) là hàm số đa thức bậc hai, bậc ba và bậc bốn thì bạn hãy sử dụng tính năng Equation (Polynomial) để tìm nghiệm của của phương trình f’(x)=0
- Còn nếu f’(x) là hàm số bất kì thì sử dụng tính năng Solver / SOLVE tìm nghiệm của của phương trình f’(x)=0
Bước 4. Lập bảng
Bước 4.1. Hàng thứ nhất.
Điền các giá trị làm cho hàm số không xác định và các nghiệm của phương trình f’(x)=0
Chú ý.
Các giá trị và các nghiệm phải được sắp xếp theo thứ tự tăng dần.
Bước 4.2. Hàng thứ hai.
Điền || tại những giá trị làm cho hàm số không xác định và điền 0 tại những nghiệm của phương trình f’(x)=0
Bước 4.3. Sử dụng tính năng CALC xét dấu f’(x)
Bước 5. Dựa vào bảng để kết luận sự biến thiên của hàm số đã cho.
#2. Cách xét sự biến thiên của hàm số bằng Casio fx 880 BTG
Ví dụ. Xét sự biến thiên (đồng biến, nghịch biến) của hàm số $f(x)=\frac{x^5}{5}-\frac{x^3}{3}+2$
Bước 1. Vì hàm số đã cho là hàm đa thức bậc 5 nên có tập xác định là R
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Bước 2. Bây giờ chúng ta sử dụng kiến thức Toán học tìm f’(x)
$f’(x)=x^4-x^2$
Bước 3. Tìm các nghiệm $x_i$ (i=1, 2, 3, …) của phương trình $f’(x)=x^4-x^2=0$
Vì $f’(x)=x^4-x^2$ là hàm đa thức bậc bốn nên chúng ta sử dụng tính năng Equation (Polynomial) để tìm nghiệm
Bước 3.1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomaial => nhấn phím OK => chọn $ax^4+bx^3+cx^2+dx+e$ => nhấn phím OK


Bước 3.2. Nhập 1 => nhấn phím EXE => nhập 0 => nhấn phím EXE => nhập -1 => nhấn phím EXE => nhập 0 => nhấn phím EXE => 0 => nhấn phím EXE
Bước 3.3. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE
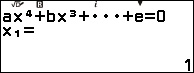
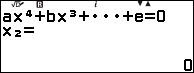
Suy ra $f’(x)=x^4-x^2$ có ba nghiệm là 1, 0, -1
Bước 4. Lập bảng biến thiên
Bước 4.1 Hàng thứ nhất
Điền -1, 0, 1
Bước 4.2. Hàng thứ hai
Điền 0 tại -1, 0, 1
Bước 4.3. Sử dụng tính năng CALC xét dấu f’(x)
Đầu tiên chúng ta sẽ xét khoảng $(-\infty, -1)$
4.3.1) Nhập $f’(x)=x^4-x^2$
4.3.2) Nhấn phím TOOLS => chọn CALC => nhấn phím OK => nhập giá trị đại diện cho khoảng $(-\infty, -1)$
Ở đây mình sẽ nhập -2 => nhấn phím EXE => nhấn phím EXE


Vì f’(-2)=12 > 0 nên khoảng $(-\infty, -1)$ mang dấu cộng (+)
Thực hiện tương tự cho các khoảng còn lại chúng ta thu được bảng biến thiên bên dưới.
Bước 5. Dựa vào bảng kết luận sự biến thiên của hàm số.
Vậy hàm số đã cho:
- Đồng biến trên các khoảng $(-\infty, -1)$ và $(1, +\infty)$
- Nghịch biến trên khoảng (-1, 1)
Xem video hướng dẫn thực hiện trên Casio 880 BTG
#3. Bấm máy tính xét sự biến thiên của hàm số (fx 580 VNX)
Ví dụ. Xét sự biến thiên của hàm số $f(x)=\frac{x^2-3x+3}{x-1}$
Bước 1. Hàm số đã cho có tập xác định là R \ {1}
Bước 2. Sử dụng kiến thức Toán học tìm f’(x)
$f’(x)=\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}$
Bước 3. Tìm các nghiệm $x_i$ (i=1, 2, 3, …) của phương trình $f’(x)=\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}=0$
Vì $f’(x)=\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}$ không là hàm đa thức (bậc hai, bậc ba và bậc bốn) nên chúng ta sử dụng tính năng Solver / SOLVE
Trước hết chúng ta có nhận xét phương trình f’(x)=0 tương đương với phương trình $\frac{(2x-3)(x-1)-(x^2-3x+3)}{(x-1)^2}=0$
Vì tử thức là đa thức bậc hai nên phương trình f’(x)=0 có tối đa hai nghiệm.
Bước 3.1. Nhập vế trái của phương trình $\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}=0$
Bước 3.2. Nhấn phím SHIFT => nhấn phím CALC => nhập giá trị x ban đầu là một số bất kì thuộc tập xác định của phương trình, mình thường nhập -3 hoặc 0 hoặc 3 => nhấn phím = => nhấn phím =
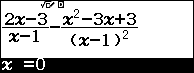
Chú ý.
Nhập -3 không tìm được nghiệm thì nhập 0, nhập 0 không tìm được nghiệm thì nhập 3
Bước 3.3. Nhập $\left(\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}\right) \div (x-0)$
Bước 3.4. Nhấn phím SHIFT => nhấn phím CALC => nhập giá trị x ban đầu là một số bất kì thuộc tập xác định của phương trình => nhấn phím = => nhấn phím =
Suy ra $f’(x)=\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}$ có hai nghiệm là 0, 2
Bước 4. Lập bảng biến thiên.
Bước 4.1. Dòng thứ nhất
Điền 0, 1, 2
Bước 4.2. Dòng thứ hai
Điền || tại 1 và điền 0 tại 0, 2
Bước 4.3. Sử dụng tính năng CALC xét dấu f’(x)
Đầu tiên chúng ta sẽ xét khoảng $(-\infty, 0)$
4.3.1) Nhập $\frac{2x-3}{x-1}-\frac{x^2-3x+3}{(x-1)^2}$
4.3.2) Nhấn phím CALC => nhập giá trị đại diện cho khoảng $(-\infty, 0)$
Ở đây mình sẽ nhập -1 => nhấn phím = => nhấn phím =
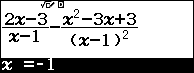
Vì $f’(-1) =\frac{3}{4}>0$ nên khoảng $(-\infty, 0)$ mang dấu cộng
Thực hiện tương tự cho các khoảng còn lại chúng ta thu được bảng bên dưới.
Bước 5. Dựa vào bảng kết luận sự biến thiên của hàm số ta kết luận được hàm số đã cho:
- Đồng biến trên các khoảng $(-\infty, 0)$ và $(2, +\infty)$
- Nghịch biến trên các khoảng (0, 1) và (1, 2)
Xem video hướng dẫn thực hiện trên Casio 580 VNX
#4. Lời kết
Okay, trên đây là cách bấm máy xét sự biến thiên của hàm số mà mình muốn chia sẻ với các bạn trong bài viết ngày hôm nay.
Phải nhắc lại lần nữa là thủ thuật sử dụng máy tính CASIO để xét sự biến thiên của hàm số này tuy chậm hơn các thủ thuật khác nhưng chắc ăn hơn nhiều các bạn ạ.
Không những vậy, bạn có thể áp dụng thủ thuật này với cả hình thức thi/kiểm tra trắc nghiệm lẫn tự luận (các thủ thuật khác chỉ khả dụng với trắc nghiệm).
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.
Đọc thêm:
- Cách khảo sát sự biến thiên của hàm phân thức (có ví dụ)
- Cách xét dấu biểu thức hữu tỉ (phân thức) bất kỳ
- Cách tìm tập xác định của hàm số (có mẹo hay)
- Cách tìm cực trị của hàm số bằng máy tính Casio 580 & 880
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống