Cách tìm tập xác định của hàm số (có mẹo hay)

Công việc đầu tiền cần làm trước khi khảo sát sự biến thiên của hàm số và vẽ đồ thị hàm số là tìm tập xác định của hàm số đó.

Công việc trên tưởng chừng như đơn giản nhưng nó lại gây không ít khó khăn cho nhiều bạn. Lý do chính là do có quá nhiều hàm số và có quá nhiều quy tắc cần phải nhớ và tuân thủ.

Vậy nên, nhằm giải quyết phần nào đó khó khăn này thì hôm nay, mình sẽ liệt kê ra toàn bộ các quy tắc cần tuân thủ và trình bày thêm một số ví dụ minh họa để giúp các bạn khắc sâu kiến thức hơn.

Kết thúc bài viết này, nếu như bạn đọc bài viết một cách nghiêm túc thì mình tin chắc là bạn có thể tìm được tập xác định của mọi hàm số, cho dù nó là hàm siêu việt hay hàm đại số, hàm sơ cấp cơ bản hay hàm sơ cấp phức hợp, …

#1. Tập xác định của hàm số là gì?

Tập xác định của một hàm số là tập hợp tất cả các giá trị thực của đối số, sao cho tất cả các phép toán có mặt trong biểu thức xác định hàm số đều có nghĩa và thực hiện được trên trường số thực.

#2. Các quy tắc cần tuân thủ khi tìm tập xác định của hàm số

Khi tìm tập xác định của hàm số chúng ta phải tuân thủ đầy đủ các quy tắc sau:

1. Mẫu thức của các phân thức phải khác không.
2. Các biểu thức nằm dưới căn bậc chẵn $(\sqrt{\square}, \sqrt[4]{\square}, \cdots,\sqrt[2k]{\square})$ phải không âm.
3. Các biểu thức cần nâng lên lũy thừa với số mũ vô tỉ, lũy thừa mà số mũ có chứa đối số phải dương.
4. Các biểu thức trong dấu Logarit phải dương.
5. Nếu biểu thức có dạng $f(x)^{g(x)}$ thì cơ số và số mũ không được đồng thời triệt tiêu.
6. Tập xác định của một hàm số là giao của các miền xác định của các hàm số thành phần.

Chú ý:
Nếu bạn là học sinh, hoặc giáo viên Trung học cơ sở thì bạn chỉ cần quan tâm đến quy tắc [1], [2], [6] bên trên thôi ha !

#3. Tập xác định của các hàm số sơ cấp cơ bản

Trước khi tìm tập xác định của các hàm số sơ cấp thì chúng ta sẽ tìm tập xác định của các hàm số sơ cấp cơ bản trước đã.

Việc làm này rất có ý nghĩa vì các hàm số sơ cấp đều được tạo thành từ các hàm số sơ cấp cơ bản.

Ví dụ. Các hàm số $y=c$ (hằng số), $y=x^n$ $(n \in N)$, $y=\sqrt[2k+1]{x}$, $y=a^x$ $(0<a \neq 1)$, $y=\sin x, y=\cos x, y=\tan x, y=\cot x$ có miền xác định là $(-\infty, +\infty)$

Ví dụ. Hàm số $y=\sqrt[2k]{x}$ có miền xác định là  $[0, +\infty)$

Ví dụ. Các hàm số $y=x^{\alpha}$ ($\alpha$ vô tỉ), $y=\log_a x$ $(0<a\neq 1, x>0)$ có miền xác định là  $(0, +\infty)$

Ví dụ. Các hàm số $y=\arcsin x, y=\arccos x$ có miền xác định là $[-1, 1]$

Ví dụ. Các hàm số $y=\tan x, y=\cot x$ lần lượt có miền xác định là $\forall x \neq \frac{\pi}{2}+k\pi, \forall x \neq k\pi$

#4. Ví dụ minh họa

Ví dụ 1. Tìm miền xác định của hàm số $y=2x+3$

Lời giải:

Hàm số $y=2x+3$ là một hàm hữu tỉ nguyên (đa thức) nên có miền xác định là $R$

Chú ý:
Tất cả các hàm hữu tỉ nguyên (đa thức) đều có tập xác định là $R$

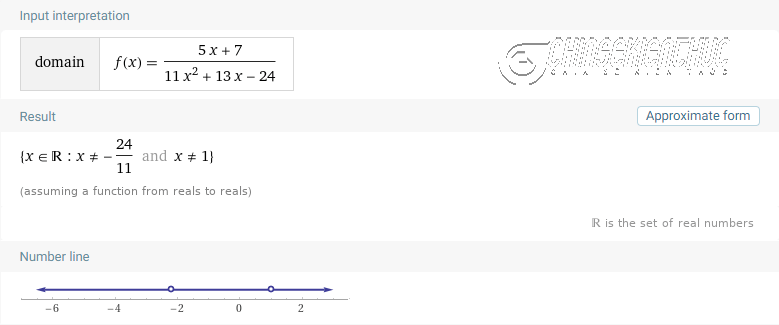
Ví dụ 2. Tìm tập xác định của hàm số $y=\frac{5x+7}{11x^2+13x-24}$

Lời giải:

Hàm số $y=\frac{5x+7}{11x^2+13x-24}$ là một hàm hữu tỉ phân (phân thức), suy ra hàm số này xác định khi $11x^2+13x-24 \neq 0$

$11x^2+13x-24 \neq 0 \Leftrightarrow \left[\begin{array}{l}x \neq 1 \\ x \neq -\frac{24}{11}\end{array}\right.$

Vậy tập xác định của hàm số đã cho là $\{x \in R: x \neq 1, x \neq -\frac{24}{11}\}$

Xem thêm:
Cách giải phương trình bậc hai

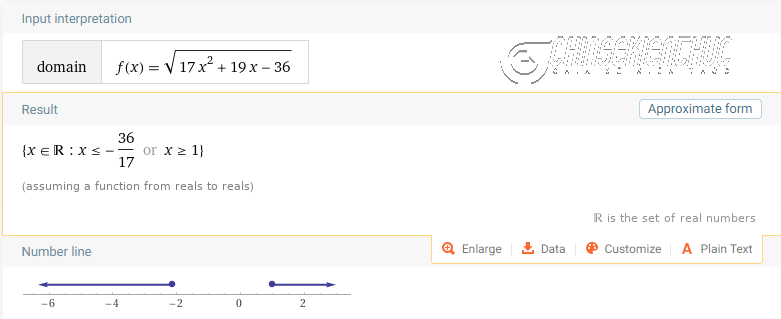
Ví dụ 3. Tìm miền xác định của hàm số $y=\sqrt{17x^2+19x-36}$

Lời giải:

Hàm số $y=\sqrt{17x^2+19x-36}$ là một hàm vô tỉ (căn bậc chẵn), suy ra hàm số này xác định khi $17x^2+19x-36 \geq 0$

$17x^2+19x-36 \geq 0 \Leftrightarrow \left[\begin{array}{l}x \geq 1 \\ x \leq -\frac{36}{17}\end{array}\right.$

Vậy tập xác định của hàm số đã cho là $\{x \in R: x \geq 1, x \leq -\frac{36}{17}\}$

Xem thêm Cách giải bất phương trình bậc hai

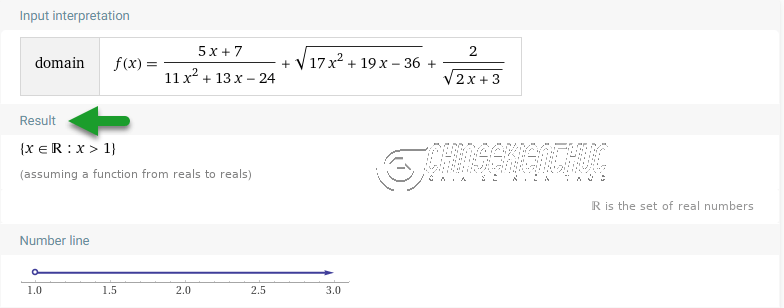
Ví dụ 4. Tìm miền xác định của hàm số $y=\frac{5x+7}{11x^2+13x-24}+\sqrt{17x^2+19x-36}+\frac{2}{\sqrt{2x+3}}$

Lời giải:

Hàm số $y=\frac{5x+7}{11x^2+13x-24}+\sqrt{17x^2+19x-36}+\frac{2}{\sqrt{2x+3}}$ là một hàm đại số sơ cấp có ba hàm số thành phần

Vậy nên, muốn tìm tập xác định của hàm số này thì chúng ta sẽ phải tìm tập xác định của từng hàm số thành phần, rồi lấy giao các tập xác định vừa tìm được.

• Hàm số thành phần $\frac{5x+7}{11x^2+13x-24}$ có miền xác định là $\{x \in R: x \neq 1, x \neq -\frac{24}{11}\}$
• Hàm số thành phần $\sqrt{17x^2+19x-36}$ có miền xác định là $\{x \in R: x \geq 1, x \leq -\frac{36}{17}\}$
• Hàm số thành phần $\frac{2}{\sqrt{2x+3}}$ có miền xác định là $\{x \in R: x > -\frac{3}{2}\}$

Vậy => tập xác định của hàm số đã cho là $\{x \in R: x>1\}$

#5. Một số chú ý về cách viết tập xác định

• Tập xác định $R$ có cách viết khác là $(-\infty, +\infty)$
• Tập xác định $\{x \in R: x \neq 1, x \neq -\frac{24}{11}\}$ có cách viết khác là $R \backslash \{1, -\frac{24}{11}\}$
• Tập xác định $\{x \in R: x \geq 1, x \leq -\frac{36}{17}\}$ có cách viết khác là $(-\infty, -\frac{36}{17}] \cup [1+\infty)$

#6. Tìm tập xác định của hàm số bằng công cụ trực tuyến WolframAlpha

Công cụ trực tuyến WolframAlpha cho phép chúng ta tìm nhanh và chính xác tập xác định của mọi hàm số.

Nếu có thể thì các bạn nên sử dụng WolframAlpha để kiểm tra tính chính xác tập xác định của hàm số, nhất là với các hàm số phức tạp.

Bước 1. Truy cập vào trang chủ của WolframAlpha theo liên kết https://www.wolframalpha.com/

Bước 2. Chọn MATH INPUT

Bước 3. Nhập domain of f(x) = <hàm số>

Ví dụ ở đây mình cần tìm tập xác định của hàm số $y=\frac{5x+7}{11x^2+13x-24}+\sqrt{17x^2+19x-36}+\frac{2}{\sqrt{2x+3}}$ thì nhập như hình bên dưới:

Bước 4. Nhấn phím Enter trên bàn phím máy tính để xem kết quả, kết quả cần tìm sẽ hiển thị tại dòng Result nha các bạn.

#7. Lời kết

Tóm lại, trong quá trình làm bài tập, khi cần tìm tập xác định của hàm số thì các bạn nên thực hiện theo tuần tự các bước gợi ý bên dưới, việc làm này sẽ giúp bạn tránh được những sai sót không đáng có:

1. Đầu tiên, bạn hãy quan sát một lượt xem hàm số đã cho có mấy hàm số thành phần.
2. Tiếp theo, bạn hãy tìm tập xác định của từng hàm số thành phần dựa vào bảy quy tắc nêu trên.
3. Cuối cùng là lấy giao của các tập xác định của các hàm số thành phần mới tìm được, nếu chưa quen thì nên vẽ từng miền xác định ra giấy rồi giao lại ha.

Ngoài ra. bạn cũng đừng quên sử dụng công cụ WolframAlpha để kiểm tra lại kết quả cuối cùng, để chắc chắn là tập xác định bạn tìm là đúng.

Hi vọng những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn