Cách phân loại biểu thức Toán học

Xin chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu về cách phân loại các phép toán sơ cấp và các biểu thức Toán học.

Đầu tiên mình sẽ trình bày khái niệm, tiếp theo là ví dụ minh họa và cuối cùng là chỉ ra những sai lầm cần tránh trong quá trình làm bài tập.

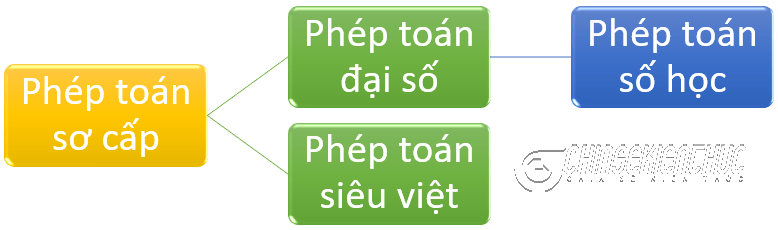
#1. Phân loại các phép toán sơ cấp

Phép cộng, trừ, nhân, chia (được gọi là bốn phép toán số học), phép nâng lên lũy thừa với số mũ hữu tỉ được gọi là các phép toán đại số.

Phép nâng lên lũy thừa với số mũ vô tỉ, phép Logarit, phép lượng giác, … được gọi là các phép toán siêu việt.

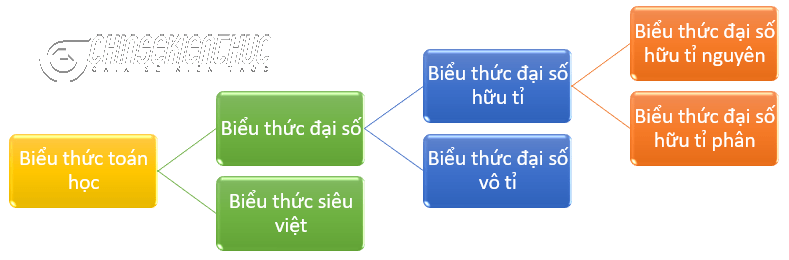
#2. Phân loại biểu thức Toán học

Một số chú ý …

• Biểu thức Đại số hữu tỉ nguyên thường được gọi là đa thức.
• Biểu thức Đại số hữu tỉ phân thường được gọi là phân thức.

#3. Ví dụ minh họa

Ví dụ 1. $A(x)=-9x^3+8x^2-\sqrt{8}x+7$, $B(x)=\frac{2x-\sqrt{6}x+8}{x+6}$, $C(x)=\frac{\sqrt{x-4}-\sqrt{x+8}}{\sqrt{x^2+7}}$ là các biểu thức đại số của đối số $x$ trên trường số thực $R$

Cụ thể hơn thì …

• $A(x)$ là biểu thức đại số hữu tỉ nguyên
• $B(x)$ là biểu thức đại số hữu tỉ phân
• $C(x)$ là biểu thức đại số vô tỉ

Ví dụ 2. $E(x)=\sin 2x+2x^2-2x+8$, $F(x)=\tan 6x+7^x-6$, $G(x)=\log (x+2)-x^{\sqrt{7}}+9$ là những biểu thức siêu việt của đối số $x$ trên trường số thực $R$

Ví dụ 3. $I(x,y)=(x+7y)^2-3xy+\frac{x-2}{y-9}+4$ là biểu thức đại số hữu tỉ phân của hai đối số $x, y$ trên trường số hữu tỉ $Q$

Ví dụ 4. $K(x,y,z)=\frac{x+9y+2z}{\sqrt{x}-\sqrt{z}}+7^{x-y}+\cos z^5$ là biểu thức siêu việt của ba đối số $x, y, z$ trên trường số hữu tỉ $Q$

#4. Những sai lầm cần tránh khi phân loại biểu thức Toán học

Để phân loại một biểu thức Toán học là đại số hay siêu việt thì chúng ta cần quan tâm đến tính chất của phép toán thực hiện trên các đối số, chứ không phải trên các hệ số.

Ví dụ 5. $L(x)=\sqrt{5}x^2+\sin (15^o)(x+9)^3-(\log_2 4)(\sqrt{x}-9)^3$

Tuy L(x) có chứa phép lượng giác, phép Logarit nhưng hai phép này không thực hiện trên đối số $x$ mà thực hiện trên hệ số thực => nên L(x) vẫn là biểu thức đại số vô tỉ.

Thật vậy, nếu thu gọn các hệ số của L(x) thì ta sẽ được $\sqrt{5}x^2+\left(\frac{\sqrt{6}-\sqrt{2}}{4}\right)(x+9)^3-2(\sqrt{x}-9)^3$

#5. Lời kết

Thay cho lời kết thì mình sẽ chia sẻ thêm với các bạn một kinh nghiệm giúp phân loại nhanh biểu thức Toán học.

Chúng ta sẽ phân loại theo trình tự các bước bên dưới (vẫn với chú ý là các phép toán thực hiện trên các đối số nha các bạn).

• Bước 1. Quan sát xem, nếu có phép nâng lên lũy thừa với số mũ vô tỉ, phép Logarit, phép lượng giác thì kết luận biểu thức siêu việt. Ngược lại (không có) thì kết luận là biểu thức đại số.
• Bước 2. Tiếp tục phân loại biểu thức đại số.
  • Bước 2.1. Quan sát xem, nếu có phép khai căn thì kết luận là biểu thức đại số vô tỉ, còn ngược lại (không có) thì kết luận biểu thức đại số hữu tỉ.
  • Bước 2.2. Tiếp tục phân loại biểu thức đại số hữu tỉ
  • Bước 2.2.1. Quan sát xem, nếu biểu thức có chứa phép chia cho các đối số thì kết luận là biểu đại số hữu tỉ phân, còn ngược lại (không có) kết luận biểu thức đại số hữu tỉ nguyên.

Hi vọng những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn