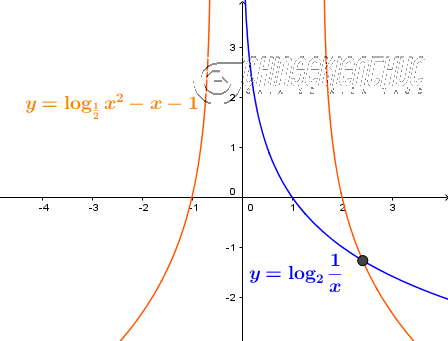Cách giải phương trình Logarit (2 dạng thường gặp nhất)

Trong quá trình làm bài tập, nhiều bài toán khi giải sẽ dẫn đến việc giải phương trình có dạng $\log_a x=m$

Phương trình có dạng $\log_a x=m$ với $a, m$ là những số thực cho trước và $0 < a \neq 1$ được gọi là phương trình Logarit.

Hôm nay chúng ta sẽ cùng nhau tìm hiểu về cách giải phương trình Logarit và hai dạng phương trình Logarit thường gặp nhất nhé !

#1. Phương trình Logarit là gì?

Phương trình Logarit là phương trình có chứa ẩn trong biểu thức dưới dấu Logarit.

Ví dụ. $\log_2 x=\frac{3}{5}, \ln x=0$ $\log_2 \frac{1}{x}=\log_{\frac{1}{2}} (x^2-x-1), \frac{6}{\log_2 2x}+\frac{4}{\log_2 x^2}=3$ là những phương trình logarit.

Chú ý: Logarit cơ số $10$ và logarit cơ số $e$ sẽ có tên riêng và kí hiệu riêng nha các bạn.

• Logarit cơ số $10$ được gọi là logarit thập phân và được ký hiệu là $\log$
• Logarit cơ số $e$ được gọi là logarit tự nhiên và được ký hiệu là $\ln$

#2. Phương trình Logarit cơ bản

Phương trình Logarit cơ bản có dạng $\log_a x=m$ với $a, m$ là một số thực cho trước và $a<0 \neq 1$

Điều kiện xác định của phương trình $\log_a x=m$ là $x>0$

Tương tự như phương trình mũ $a^x=m$ thì việc giải phương trình Logarit $\log_a x=m$ cũng rất đơn giản.

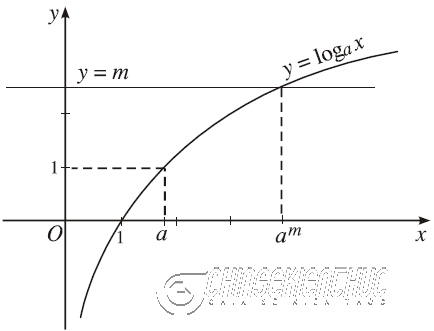
Với mỗi giá trị tùy ý của $m$ phương trình $\log_a x=m$ luôn luôn có một nghiệm duy nhất là $x=a^m$, hay nói cách khác $\forall m \in (- \infty; + \infty), \log_a x=m \Leftrightarrow x=a^m$

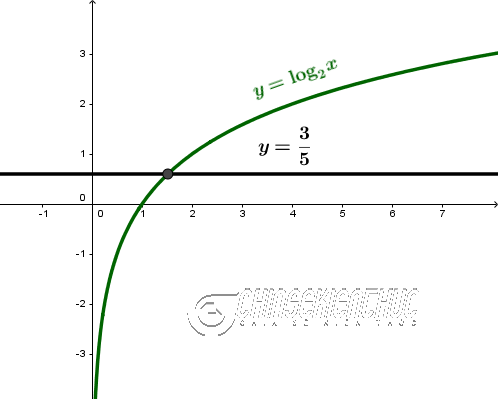
Ví dụ 1. Giải phương trình $\log_2 x=\frac{3}{5}$

Lời giải:

$\log_2 x=\frac{3}{5} \Leftrightarrow x=2^{\frac{3}{5}}$

Vậy tập nghiệm của phương trình đã cho là $\{2^{\frac{3}{5}}\}$

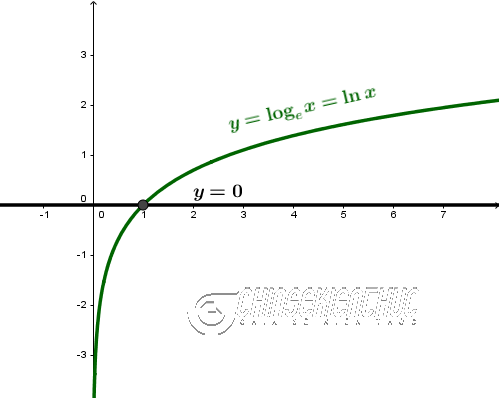
Ví dụ 2. Giải phương trình $\ln x=0$

Lời giải:

$\ln x=0 \Leftrightarrow x=e^0 \Leftrightarrow x=1$

Vậy tập nghiệm của phương trình đã cho là $\{1\}$

#3. Cách giải phương trình Logarit thường gặp

Khi giải các phương trình logarit chúng ta thường cố gắng biến đổi phương trình đã cho thành một trong hai dạng bên dưới.

Tại sao lại như vậy?

Vâng, đơn giản là vì hai dạng bên dưới là hai dạng dễ giải nhất trong tất cả các dạng thường gặp !

Dạng 1. Các phương trình có thể giải được bằng cách đưa về cùng cơ số

Trước hết chúng ta thừa nhận mệnh đề nếu $f(x)>0, g(x)>0$ thì $\log_a f(x)=\log_a g(x) \Leftrightarrow f(x)=g(x)$

Mệnh đề trên cho phép chúng ta giải một số dạng phương trình logarit bằng cách đưa các logarit trong phương trình về các logarit với cùng một cơ số.

Ví dụ 3. Giải phương trình $\log_2 \frac{1}{x}=\log_{\frac{1}{2}} (x^2-x-1)$ $(*)$

Gợi ý:

• Tìm điều kiện xác định của phương trình
• Biến đổi sao cho phương trình về cùng cơ số

Lời giải:

Điều kiện xác định của phương trình là $\left\{\begin{array}{l}\frac{1}{x}>0 \\ x^2-x-1>0\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x>0 \\ \left[\begin{array}{l}x>\frac{1+\sqrt{5}}{2} \\ x<\frac{1-\sqrt{5}}{2}\end{array}\right.\end{array}\right. \Leftrightarrow x>\frac{1+\sqrt{5}}{2}$

Dễ thấy $\log_2 \frac{1}{x}=\log_\frac{1}{2} x$

$(*) \Leftrightarrow \log_\frac{1}{2} x=\log_{\frac{1}{2}} (x^2-x-1) \Leftrightarrow x=x^2-x-1$

Kết hợp với điều kiện $x>\frac{1+\sqrt{5}}{2}$ ta có hệ

$\left\{\begin{array}{l}x>\frac{1+\sqrt{5}}{2} \\ x=x^2-x-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x>\frac{1+\sqrt{5}}{2} \\ \left[\begin{array}{l}x=1+\sqrt{2} \\ x=1-\sqrt{2} \end{array}\right.\end{array}\right. \Leftrightarrow x=1+\sqrt{2}$

Vậy tập nghiệm của phương trình đã cho là $\{1+\sqrt{2}\}$

Xem thêm:

• Cách giải phương trình bậc hai
• Cách giải bất phương trình bậc hai

Dạng 2. Các phương trình có thể giải được bằng cách đặt ẩn phụ

Bằng cách đặt ẩn phụ thích hợp thì chúng ta có thể chuyển từ việc giải một phương trình Logarit phức tạp sang việc giải các phương trình Logarit đơn giản.

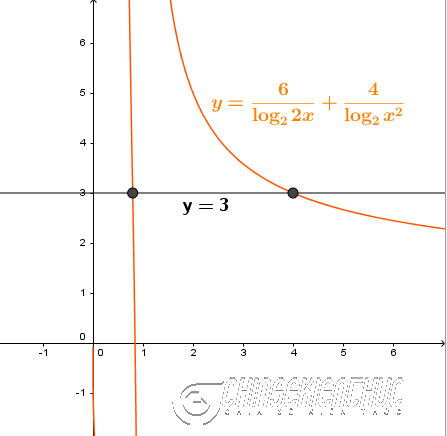
Ví dụ 4. Giải phương trình $\frac{6}{\log_2 2x}+\frac{4}{\log_2 x^2}=3$ $(*)$

Lời giải:

Điều kiện xác định của phương trình $(*)$ là $\left\{\begin{array}{l}\log_2 2x \neq 0 \\ \log_2 x^2 \neq 0 \\ 2x>0 \\x^2>0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \neq \frac{1}{2} \\ \left[\begin{array}{l}x \neq 1 \\ x \neq -1\end{array}\right. \\ x>0 \\ \left[\begin{array}{l}x>0 \\ x<0 \end{array}\right. \end{array}\right. \Leftrightarrow \left\{\begin{array}{l}x \neq \frac{1}{2} \\ x \neq 1 \\ x>0 \end{array}\right.$

Với các điều kiện trên phương trình $(*)$ tương đương với $\frac{6}{1+\log_2 x}+\frac{4}{2 \log_2 x}=3$ $(**)$

Đặt $t=\log_2 x$ phương trình $(**)$ trở thành $\frac{6}{1+t}+\frac{4}{2t}=3 \Leftrightarrow \frac{6}{1+t}+\frac{2}{t}=3$ $(***)$

Điều kiện của phương trình $(***)$ là $t \neq -1, t \neq 0$

Quy đồng mẫu ta được phương trình $\frac{6t}{(1+t)t}+\frac{2(1+t)}{t(1+t)}=\frac{3(1+t)t}{(1+t)t}$

Khử mẫu ta được phương trình $6t+2(1+t)=3(1+t)t \Leftrightarrow -3t^2+5t+2=0 \Leftrightarrow \left[\begin{array}{l}t=2 \\ t=-\frac{1}{3} \end{array}\right.$

• Với $t=2$ ta được phương trình $2=\log_2 x \Leftrightarrow x=2^2 \Leftrightarrow x=4$
• Với $t=-\frac{1}{3}$ ta được phương trình $-\frac{1}{3}=\log_2 x \Leftrightarrow x=2^{-\frac{1}{3}} \Leftrightarrow x=\frac{1}{\sqrt[3]{2}}$

Vậy tập nghiệm của phương trình đã cho là $\left\{4, \frac{1}{\sqrt[3]{2}}\right\}$

Xem thêm:
Cách giải phương trình chứa ẩn ở mẫu

#4. Lời kết

Okay, như vậy là mình đã hướng dẫn xong cho bạn cách giải phương trình Logarit thường gặp nhất rồi đó.

Thay cho lời kết thì mình xin gửi đến các bạn một chú ý quạn trọng đó là:

Khi giải phương trình Logarit bạn cần tìm chính xác điều kiện xác định của phương trình, nếu tìm sai thì rất có thể tập nghiệm sẽ sai theo.

Đó là lý do tại sao ở Ví dụ 3 và Ví dụ 4 mình tìm điều kiện xác định kỹ lưỡng đến như vậy. Okay, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nha!

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn