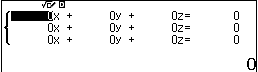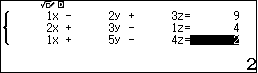2 cách giải hệ ba phương trình bậc nhất ba ẩn, rất dễ !

Xin chào tất cả các bạn !

Tiếp nói mạch kiến thức về hệ phương trình, hôm nay mình sẽ hướng dẫn các bạn giải hệ ba phương trình bậc nhất ba ẩn bằng phương pháp Toán học và phương pháp sử dụng máy tính cầm tay (Casio).

#1. Hệ ba phương trình bậc nhất ba ẩn là gì?

Hệ ba phương trình bậc nhất ba ẩn có dạng $\left\{\begin{array}{l} a_1x+b_1y+c_1z=d_1 \\ a_2x+b_2y+c_2z=d_2 \\ a_3x+b_3y+c_3z=d_3 \end{array}\right.$

Trong đó:

• $x, y, z$ là ba ẩn
• $a_i, b_i, c_i, d_i$ với $i=1, 2, 3$ là các số thực cho trước, được gọi là các hệ số.

Nếu bộ ba số $(x_0, y_0, z_0)$ thỏa mãn đồng thời cả ba phương trình của hệ thì bộ ba số $(x_0, y_0, z_0)$ được gọi là nghiệm.

Giải hệ ba phương trình là tìm tất cả các nghiệm của nó.

#2. Các cách giải hệ ba phương trình bậc nhất ba ẩn

Có khá nhiều phương pháp để giải hệ ba phương trình bậc nhất ba ẩn.

Tuy nhiên, phép biến đổi tương đương chuyển về dạng tam giác là một trong những phương pháp được sử dụng nhiều nhất.

Phương pháp giải này do nhà Toán học tài ba người Đức Gauss đề xuất.

#3. Bài tập ví dụ

Giải hệ ba phương trình bậc nhất ba ẩn $\left\{\begin{array}{l} x-2y+3z=9 \qquad (1) \\ 2x+3y-z=4 \qquad (2) \\ x+5y-4z=2 \qquad (3) \end{array}\right.$

3.1. Sử dụng phương pháp Toán học

Nhân cả hai vế của phương trình ⁽³⁾ với $-2$, sau đó cộng vế với vế của phương trình nhận được với phương trình ⁽²⁾, giữ nguyên các phương trình ⁽¹⁾ và ⁽²⁾ ta được hệ:

$\left\{\begin{array}{l} x-2y+3z=9 \qquad (1) \\ 2x+3y-z=4 \qquad (2) \\ -7y+7z=0 \qquad (3.1) \end{array}\right.$

Nhân hai vế của phương trình ⁽¹⁾ với $-2$, cộng vế với vế của phương trình nhận được với phương trình ⁽²⁾, giữ nguyên các phương trình ⁽¹⁾ và ^(3.1) ta được hệ:

$\left\{\begin{array}{l} x-2y+3z=9 \qquad (1) \\ 7y-7z=-14 \qquad (2.1) \\ -7y+7z=0 \qquad (3.1) \end{array}\right.$

Cộng vế với vế của phương trình ^(2.1) với phương trình ^(3.1), giữ nguyên các phương trình ⁽¹⁾ và ^(2.1) ta được hệ:

$\left\{\begin{array}{l} x-2y+3z=9 \qquad (1) \\ 7y-7z=-14 \qquad (2.1) \\ 0y+0z=-14 \qquad (3.2) \end{array}\right.$

Vì phương trình ^(3.2) vô nghiệm nên hệ phương trình đã cho vô nghiệm.

3.2. Sử dụng máy tính Casio

Mình sẽ hướng dẫn thực hành trên máy tính cầm tay CASIO fx 580 VN X, với các dòng máy tính cầm tay khác, các bạn thực hiện tương tự ha.

Bước 1. Lần lượt nhấn các phím  để mở tính năng giải hệ ba phương trình bậc nhất ba ẩn

Bước 2. Lần lượt nhấn các phím   để nhập các hệ số

Bước 3. Nhấn phím =

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Vậy hệ phương trình đã cho vô nghiệm !

Chú ý:
Nếu máy tính cầm tay CASIO fx 580 VN X thông báo Infinite Solution thì hệ ba phương trình vô số nghiệm

#4. Bài tập 

Bạn hãy sử dụng phương pháp Toán học và phương pháp máy tính cầm tay giải các hệ ba phương trình bậc nhất ba ẩn:

1. a) $\left\{\begin{array}{l} x-2y=1 \\ x+2y-z=-2 \\ x-3y+z=3 \end{array}\right.$
2. b) $\left\{\begin{array}{l} 3x-y+2z=2 \\ x+2y-z=1 \\ 2x-3y+3z=2 \end{array}\right.$
3. c) $\left\{\begin{array}{l} x-y+z=0 \\ x-4y+2z=-1 \\ 4x-y+3z=1 \end{array}\right.$

Đáp án:

1. a) $\left(\frac{1}{3}, -\frac{1}{3}, \frac{5}{3}\right)$
2. b) vô nghiệm
3. c) vô số nghiệm

#5. Lời kết

Giải hệ ba phương trình bậc nhất ba ẩn bằng phương pháp Gauss là phương pháp tổng quát nhất, kinh điển nhất khi thực hiện giải hệ phương trình.

Phương pháp này ngoài giải được hệ ba phương trình bậc nhất ba ẩn ra thì nó còn giải được hệ bốn phương trình, năm phương trình, … nữa.

Còn phương pháp sử dụng máy tính cầm tay thì tính đến thời điểm hiện tại chỉ giải được tối đa là hệ bốn phương trình bậc nhất bốn ẩn.

Okay, hi vọng là những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !

Đọc thêm:

• 2 cách giải bất phương trình bậc nhất một ẩn (có ví dụ)
• 3 cách giải hệ phương trình đối xứng (có ví dụ dễ hiểu)
• 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn
• Cách GIẢI và BIỆN LUẬN phương trình bậc nhất một ẩn

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn