3 cách giải hệ phương trình đối xứng (có ví dụ dễ hiểu)

Trong chương trình Toán học Trung học, ngoài hệ phương trình tuyến tính (hệ hai phương trình bậc nhất hai ẩn, hệ ba phương trình bậc nhất ba ẩn) thì chúng ta còn gặp một số loại hệ phương trình khác nữa cũng quan trọng không kém, thường gặp nhất chính là hệ phương trình đối xứng.

Người ta thường chia hệ phương trình đối xứng thành hai loại, tuy nhiên, trong phạm vi ngắn gọn của bài viết này mình chỉ trình bày loại 1, còn loại 2 thì các bạn có thể tự tìm hiểu thêm ha.

I. Một vài kiến thức cần ôn lại

Để giải tốt hệ phương trình đối xứng thì bạn cần ôn lại các mảng kiến thức bên dưới nếu bạn không nhớ, hoặc nhớ không rõ ràng bạn nhé:

• Đẳng thức đối xứng, chủ yếu là hằng đẳng thức
• Cách giải phương trình đa thức, chủ yếu là phương trình bậc hai
• Cách giải hệ phương trình tuyến tính, chủ yếu là hệ hai phương trình hai ẩn
• Phát biểu / thuộc được hệ thức Viét của phương trình bậc hai

II. Các bước giải hệ phương trình đối xứng

Bước 1. Dựa vào các hằng đẳng thức đáng nhớ biểu diễn các phương trình của hệ thành tổng $x+y$, tích $xy$

Bước 2. Đặt $S=x+y, P=xy$

Bước 3. Giải hệ phương trình với hai ẩn mới là $S, P$

Bước 4. Tương ứng với mỗi nghiệm thỏa mãn điều kiện $S^2-4P \geq 0$ chúng ta sẽ giải phương trình bậc hai $X^2-SX+P=0$

Nghiệm của phương trình $X^2-SX+P=0$ chính là nghiệm của hệ phương trình đã cho

III. Bài tập ví dụ

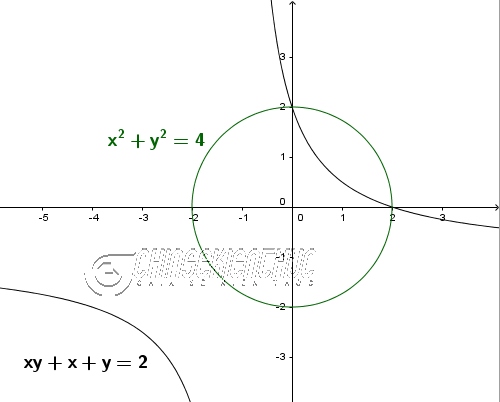
Ví dụ 1. Giải hệ phương trình $\left\{\begin{array}{l} x+y+xy=2 \\ x^2+y^2=4 \end{array}\right.$

Cách #1. Sử dụng kiến thức phương trình đối xứng

$\left\{\begin{array}{l} x+y+xy=2 \\ x^2+y^2=4 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l} x+y+xy=2 \\ (x+y)^2-2xy=4 \end{array}\right.$

Đặt $S=x+y, P=xy$

Lúc này ta được hệ phương trình $\left\{\begin{array}{l} S+P=2 \\ S^2-2P=4 \end{array}\right.$

$\left\{\begin{array}{l} S+P=2 \\ S^2-2P=4 \end{array}\right.\Leftrightarrow \left\{\begin{array}{l} P=2-S \\ S^2-2(2-S)=4 \end{array}\right.\Leftrightarrow \left\{\begin{array}{l} P=2-S \\ S^2+2S-8=0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l} P=2-S \\ \left[\begin{array}{l} S=2 \\ S=-4 \end{array}\right. \end{array}\right.$

• Với $S=2$ thì $P=0$
• Với $S=-4$ thì $P=6$

Nghiệm $(-4, 6)$ không thỏa mãn điều kiện $S^2-4P \geq 0$ nên loại ngay không cần giải.

Với $S=2$ thì $P=0$, ta được phương trình $X^2-2X=0$

Giải phương trình bậc hai $X^2-2X=0$ ta được hai nghiệm là $2, 0$

Vậy nghiệm của hệ phương trình đã cho là $(2, 0)$ và $(0, 2)$

Cách #2. Sử dụng phương pháp thế

Việc biểu diễn $x$ theo $y$ hoặc $y$ theo $x$ khá phức tạp, suy ra cách này không tối ưu.

Cách #3. Sử dụng phương pháp đồ thị hàm số

Việc vẽ đồ thị của hàm số $x+y+xy=2$ khá phức tạp, suy ra cách này cũng không tối ưu nốt.

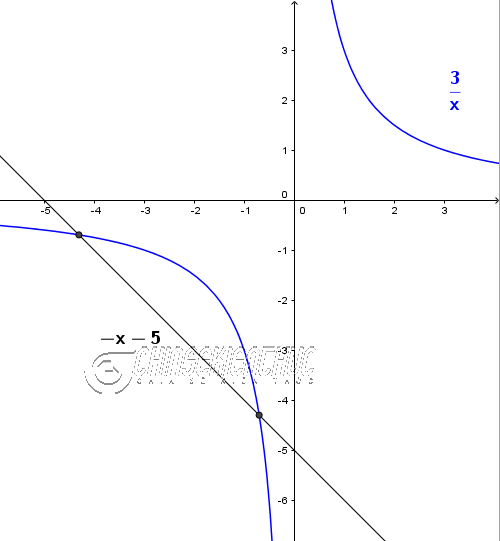
Ví dụ 2. Giải hệ phương trình $\left\{\begin{array}{l} x+y=-5 \\ xy=3 \end{array}\right.$

Cách #1. Sử dụng kiến thức phương trình đối xứng

Đặt $S=x+y, P=xy$

Lúc này ta được hệ phương trình $\left\{\begin{array}{l} S=-5 \\ P=3 \end{array}\right.$

$S=-5$ và $P=3$ thỏa mãn điều kiện $S^2-4P \geq 0$

Áp dụng định lý Viét đảo ta được phương trình $X^2+5X+3=0$

Giải phương trình bậc hai $X^2+5X+3=0$ ta được hai nghiệm là $\frac{-5+\sqrt{13}}{2}, \frac{-5-\sqrt{13}}{2}$

Vậy nghiệm của hệ phương trình đã cho là $\left(\frac{-5+\sqrt{13}}{2}, \frac{-5-\sqrt{13}}{2}\right)$ và $\left(\frac{-5-\sqrt{13}}{2}, \frac{-5+\sqrt{13}}{2}\right)$

Cách #2. Sử dụng phương pháp thế

$\left\{\begin{array}{l} x+y=-5 \\ xy=3 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l} x=-5-y \\ y(-5-y)=3\end{array}\right. \Leftrightarrow \left\{\begin{array}{l} x=-5-y \\ -5y-y^2-3=0\end{array}\right.\Leftrightarrow \left\{\begin{array}{l} x=-5-y \\ \left[\begin{array}{l} y=\frac{-5+\sqrt{13}}{2} \\ y=\frac{-5-\sqrt{13}}{2} \end{array}\right.\end{array}\right.$

• Với $y=\frac{-5+\sqrt{13}}{2}$ thì $x=\frac{-5-\sqrt{13}}{2}$
• Với $y=\frac{-5-\sqrt{13}}{2}$ thì $x=\frac{-5+\sqrt{13}}{2}$

Vậy nghiệm của hệ phương trình đã cho là $\left(\frac{-5+\sqrt{13}}{2}, \frac{-5-\sqrt{13}}{2}\right)$ và $\left(\frac{-5-\sqrt{13}}{2}, \frac{-5+\sqrt{13}}{2}\right)$

Cách #3. Sử dụng phương pháp đồ thị hàm số

Việc vẽ đồ thị của hàm số $xy=3$ khá phức tạp, suy ra cách này không tối ưu.

Ví dụ 3. Giải hệ phương trình $\left\{\begin{array}{l} x+y =2 \\ x^2+y^2=4 \end{array}\right.$

Cách 1 và Cách 2 hoàn toàn tương tự với Ví dụ 1, Ví dụ 2

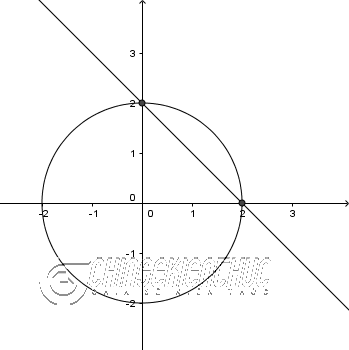
Cách 3. Sử dụng phương pháp đồ thị hàm số

Dễ thấy, $x+y=2$ là một phương trình đường thẳng, còn $x^2+y^2=4$ là một phương trình đường tròn.

Cả hai đồ thị của hai phương trình này đều là cơ bản và có thể vẽ được một cách dễ dàng.

Lời giải:

Cho $x=0$ suy ra $y=2$

Cho $x=1$ suy ra $y=1$

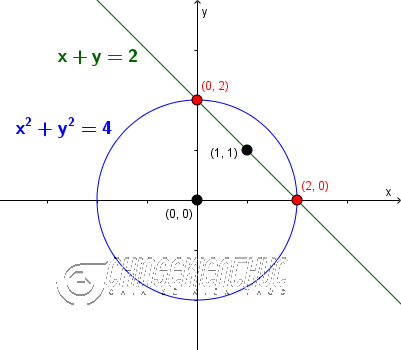
Suy ra điểm $(0, 2)$ và $(1, 1)$ là hai điểm mà phương trình đường thẳng $x+y=2$ đi qua.

Phương trình đường tròn đã cho $x^2+y^2=4 \Leftrightarrow (x-0)^2+(y-0)^2=2^2$. Suy ra tâm và bán kính của đường tròn đã cho lần lượt là $(0, 0)$ và $2$

Dựa vào đồ thị hàm số chúng ta dự đoán được $(0, 2)$ và $(2, 0)$ là nghiệm của hệ phương trình đã cho.

Thử lại với $x=0, y=2$ và $x=2, y=0$ ta thấy chúng đều thỏa mãn hệ phương trình đã cho.

Vậy nghiệm của hệ phương trình đã cho là $(0, 2)$ và $(2, 0)$

IV. Lời kết

Okay, trên đây là 3 cách giải hệ phương trình đối xứng mà mình muốn chia sẻ đến các bạn.

Trong ba cách này thì …

• Cách 1 là tối ưu nhất với đại đa số các hệ phương trình đối xứng.
• Cách 2 chỉ tối ưu khi chúng ta có thể biểu diễn $x$ theo $y$ hoặc $y$ theo $x$ một cách dễ dàng.
• Cách 3 chỉ nên sử dụng khi các hệ số của hệ phương trình là số nguyên và hàm số là các hàm đại số sơ cấp thường gặp như đường thẳng, Parabol, đường tròn..

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết khác !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn