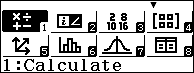Phương trình bậc nhất một ẩn là một trong những phương trình cơ bản nhất của Đại số sơ cấp.
Bằng chứng là ngay từ những năm Trung học cơ sở thì chúng ta đã được thầy (cô) giáo của mình giảng dạy về phương trình này rồi.
Và hôm này chúng ta sẽ cùng nhau ôn lại cách giải, cũng như cách biện luận phương trình bậc nhất một ẩn và tìm hiểu thêm cách giải bằng máy tính CASIO nhé.
Mục Lục Nội Dung
#1. Phương trình bậc nhất một ẩn là gì?
Phương trình bậc nhất một ẩn là phương trình có dạng $ax+b=0$ (với a, b là những số thực cho trước, a khác 0)
Ví dụ: $2x+3=0, -5x+7=0, -11x-13=0$ là những phương trình bậc nhất một ẩn.
#2. Cách giải phương trình bậc nhất một ẩn
Phương pháp #1. Dựa vào kiến thức Toán học
Bước 1: Xác định chính xác các hệ số a, b
Bước 2: Áp dụng công thức nghiệm x = $\frac{-b}{a}$
Bước 3: Kết luận
Chú ý: Hệ số đứng trước x là a, còn lại là b
Ở đây mình chỉ trình bày công thức nghiệm, không trình bày quy tắc chuyển vế, quy tắc nhân với một số vì bản chất của công thức nghiệm được suy ra từ hai quy tắc trên.
Ví dụ 1. Giải phương trình $2x+3=0$
Lời giải:
$a=2, b=3$
$2x+3=0 \Leftrightarrow x=\frac{-3}{2}$
Vậy phương trình đã cho có nghiệm duy nhất là $\frac{-3}{2}$
Ví dụ 2. Giải phương trình $7-5x=0$
Lời giải:
$a=-5, b=7$
$7-5x=0 \Leftrightarrow x=\frac{-7}{-5} \Leftrightarrow x=\frac{7}{5}$
Vậy phương trình đã cho có nghiệm duy nhất là $\frac{7}{5}$
Ví dụ 3. Giải phương trình $x+\frac{11}{13}=0$
Lời giải:
$a=1, b=\frac{11}{13}$
$x+\frac{11}{13}=0 \Leftrightarrow x=\frac{-\frac{11}{13}}{1} \Leftrightarrow x=-\frac{11}{13}$
Vậy phương trình đã cho có nghiệm duy nhất là $-\frac{11}{13}$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Ví dụ 4. Giải phương trình $17+\frac{x}{23}=0$
Lời giải:
$a=\frac{1}{23}, b=17$
$17+\frac{x}{23}=0 \Leftrightarrow x=\frac{-17}{\frac{1}{23}} \Leftrightarrow x=-391$
Vậy phương trình đã cho có nghiệm duy nhất là $-391$
Phương pháp #2. Sử dụng máy tính CASIO để giải
Bước 1: Chọn phương thức tính toán Calculate
NOTE: Chúng ta cần đảm bảo rằng phương thức thức tính toán Calculate đang được chọn vì tính năng Solve (tính năng dò tìm nghiệm của phương trình) chỉ hoạt động được trong phương thức tính toán này
Bước 2: Nhập phương trình …
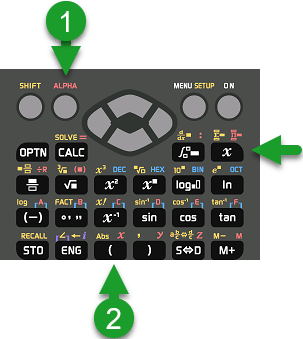
Bước 2.1: Ẩn x được nhập vào bằng cách nhấn phím x, hoặc nhấn phím ALPHA rồi nhấn phím (
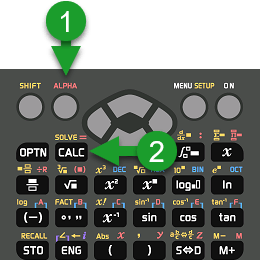
Bước 2.2: Dấu = của phương trình được nhập vào bằng cách nhấn phím ALPHA => rồi nhấn phím CALC
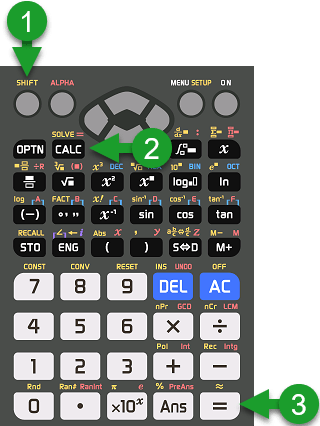
Bước 3: Tiến hành dò tìm nghiệm, nhấn phím SHIFT => rồi nhấn phím CALC => nhấn phím =
Ví dụ 5. Giải phương trình $2x+3=0$
Vậy nghiệm của phương trình đã cho là $-1.5$ hay $-\frac{3}{2}$
Chú ý:
Ngay sau khi nhấn phím SHIFT rồi nhấn phím CALC (phím SOLVE) máy tính sẽ yêu cầu chúng ta nhập giá trị x ban đầu.
Vì phương trình đang dò tìm nghiệm là phương trình bậc nhất nên giá trị x ban đầu này không quan trọng, bạn cứ nhấn tiếp phím =
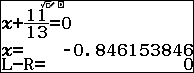
Ví dụ 6. Giải phương trình $x+\frac{11}{13}=0$
Chú ý: Ở phương trình này nghiệm hiển thị dưới dạng thập phân, để hiển thị dưới dạng phân số bạn hãy nhấn phím AC => nhấn phím Ans => nhấn phím =
Vậy nghiệm của phương trình đã cho là $-\frac{11}{13}$
#3. Cách biện luận phương trình bậc nhất một ẩn
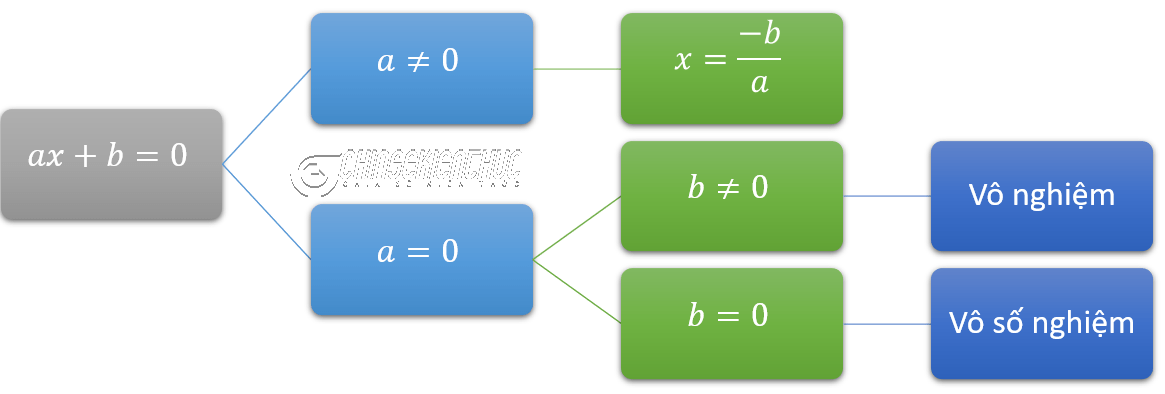
Chúng ta sẽ biện luận nghiệm của phương trình bậc nhất một ẩn theo các trường hợp như sơ đồ.
Biện luận nghiệm của phương trình bậc nhất một ẩn $ax+b=0$
- Nếu a khác 0 phương trình đã cho có một nghiệm duy nhất $x=\frac{-b}{a}$
- Nếu a bằng 0 và …
- b khác 0 thì phương trình đã cho vô nghiệm.
- b bằng 0 thì phương trình đã cho vô số nghiệm.
Ví dụ 7. Giải và biện luận phương trình $(m-1)x+(m-2)=0$
Lời giải:
Trường hợp 1: $m-1 \neq 0 \Leftrightarrow m \neq 1$
Lúc bấy giờ phương trình đã cho có một nghiệm duy nhất là $x=\frac{-(m-2)}{m-1}=\frac{-m+2}{m-1}$
Trường hợp 2: $m-1 = 0 \Leftrightarrow m = 1$, phương trình đã cho trở thành $(1-1)x+(1-2)=0 \Leftrightarrow 0x-1=0$
Phương trình đã cho vô nghiệm:
#4. Lời kết
Việc giải phương trình bậc nhất một ẩn không có gì khó khăn cả, thậm chí có thể giải được dễ dàng và chính xác nhờ vào sự hỗ trợ của máy tính bỏ túi CASIO.
Tương tự như vậy, việc biện luận cũng thế, nhiều bạn cho là khó nhưng thực sự nó cũng đơn giản như việc giải mà thôi. Chỉ có một lưu ý là khi hệ số đứng trước a là tham số thì cần xét hai trường hợp là bằng không và khác không. Vậy thôi !
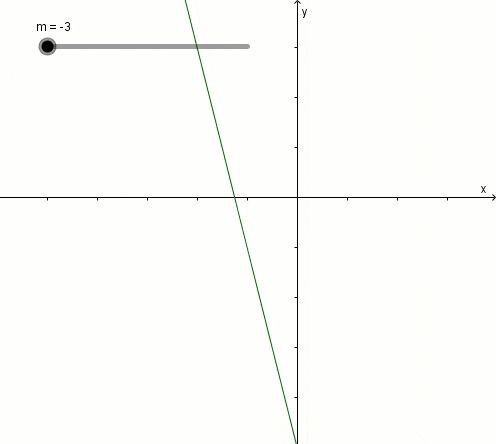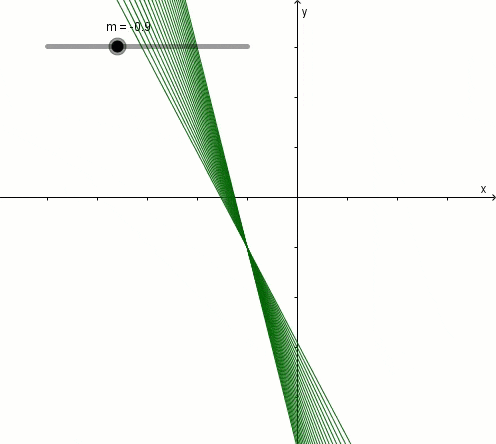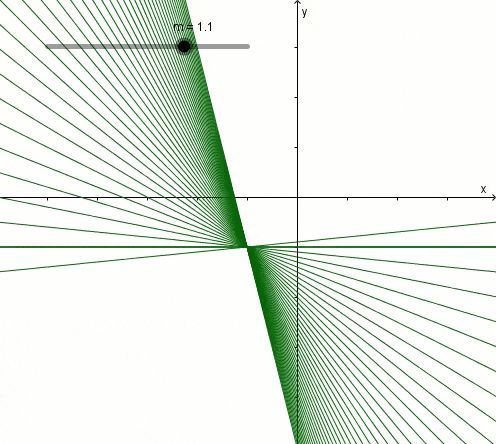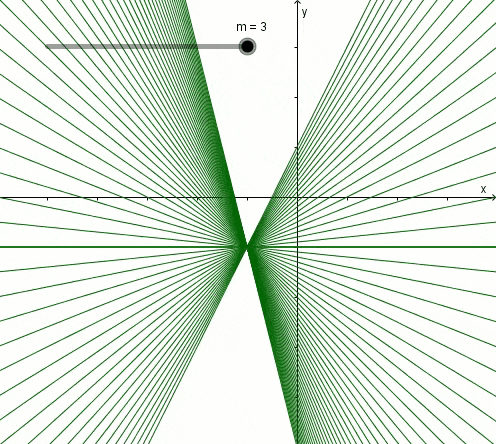
Ngoài ra, nếu bạn là sinh viên sư phạm, hoặc là giáo viên thì bạn có thể sử dụng thêm công cụ Slider của phần mềm GeoGebra để tạo mô hình minh họa trực quan tập nghiệm của phương trình để học sinh tiện theo dõi hơn, cũng như sẽ dễ hiểu hơn.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- 7 cách giải phương trình bậc hai đơn giản, hiệu quả
- 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn
- Hằng đẳng thức là gì? 7 hằng đẳng thức đáng nhớ (có ví dụ)
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống