Cách phân loại các hàm số sơ cấp

Vâng, tương tự như các biểu thức Toán học, các hàm số sơ cấp cũng cần được phân loại một cách cụ thể.

Nếu như việc phân loại các biểu thức Toán học chỉ mang tính chất bổ trợ thì việc phân loại các hàm số sơ cấp có nhiều giá trị hơn.

Chẳng hạn như:

• “Hàm hữu tỉ nguyên có tập xác định là $R$”
• “Hàm hữu tỉ nguyên liên tục trên $R$”…

Các bạn phải biết được hàm hữu tỉ nguyên là hàm như thế nào mới có thể vận dụng được các mệnh đề trên.

Tóm lại, khi người ta dùng “khái niệm” thì bạn phải phát biểu được khái niệm thì mới có thể tự học và tự nghiên cứu được. Đó cũng chính là lý do ra đời của bài viết này, và cũng là lý do tại sao chúng ta phải biết cách phân loại các hàm số sơ cấp.

#1. Hàm sơ cấp cơ bản là gì?

Không biết vì lý do gì mà các tài liệu tham khảo, thậm chí giáo trình cũng không phát biểu trực tiếp định nghĩa hàm sơ cấp cơ bản.

Theo mình, nguyên nhân có thể là do định nghĩa khó hiểu, dài dòng, … không phù hợp với đại đa số các bạn đọc.

Tương tự như tài liệu tham khảo, giáo trình… thì ở đây mình cũng không định nghĩa trực tiếp hàm số sơ cấp cơ bản là gì, mà sẽ liệt kê ra toàn bộ các hàm sơ cấp cơ bản để các bạn dễ hình dung hơn.

Dưới đây là danh sách của chúng:

• $y=c$ (hằng số), $y=x^n$ $(n \in N)$, $y=\sqrt[n]{x}$, $y=x^\alpha$ $(\alpha$ vô tỉ)
• $y=a^x$ $(0<a\neq1)$, $y=\log_a x$ $(0<a\neq1, x>0)$
• $y=\sin x, y=\cos x, y=\tan x, y=\cot x$
• $y=\arcsin x, y=\arccos x, y=\arctan x$, y=arccot x

#2. Hàm sơ cấp phức hợp là gì?

Hàm số sơ cấp phức hợp là hàm số thu được bằng cách thực hiện liên tiếp một số hữu hạn các hàm số sơ cấp cơ bản.

Các hàm số được tạo thành từ các hàm số sơ cấp phức hợp bằng một số hữu hạn các phép toán đại số, siêu việt được gọi là các hàm số sơ cấp.

Ví dụ. $y=6x^2+\sqrt{3x-3}+\sin(8x-7)^2+\log_2 (\sqrt{x+2}-7)$ là một hàm số sơ cấp

#3. Cách phân loại các hàm số sơ cấp

Trước hết, chúng ta cần biết mọi hàm số sơ cấp đều có dạng $y=f(x)$ và mỗi f(x) lại là một biểu thức Toán học

Vậy chúng ta có thể phân loại các hàm sơ cấp dựa theo loại f(x)

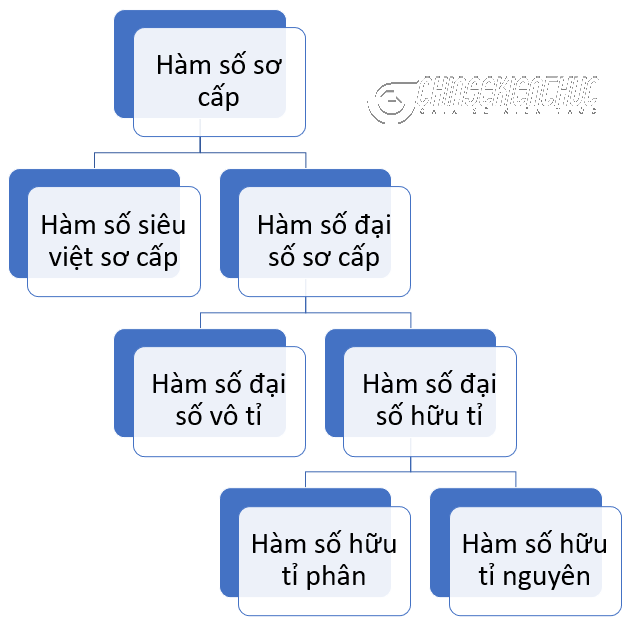
Dựa theo các kiến thức trong bài viết cách phân loại các biểu thức Toán học thì chúng ta sẽ phân loại các hàm sơ cấp như sơ đồ bên dưới.

#4. Ví dụ minh họa

Ví dụ 1. $y=x^{\sqrt{3}}, y=\log_3 (9+8x)+\arctan x, y=3^x+7-\sqrt{\tan x}$ làm các hàm siêu việt sơ cấp

Ví dụ 2. $y=x^3-7x^2, y=\frac{x^2+5}{x-3}, y=\sqrt{x+\sqrt{x}}-8\sqrt[3]{x-4}$ là các hàm đại số sơ cấp

Cụ thể hơn là …

• $y=x^3-7x^2$ là hàm hữu tỉ nguyên
• $y=\frac{x^2+5}{x-3}$ là hàm hữu tỉ phân
• $y=\sqrt{x+\sqrt{x}}-8\sqrt[3]{x-4}$ là hàm vô tỉ

#5. Sai lầm cần tránh

Khi tiến hành phân loại các hàm số sơ cấp thì chúng ta cần chú ý đến bản chất của hàm số chứ không phải hình thức.

• Hàm số $y=2^{\log_2 (6+x^2)}$ không phải là hàm số siêu việt vì nó có thể viết lại thành $y=6+x^2$
• Hàm số $y=\sqrt[3]{(x^2-3)^3}$ không phải hàm số vô tỉ vì nó có thể viết lại thành $y=x^2-3$

#6. Lời kết

Việc phân loại hàm số sơ cấp không có gì khó khăn cả, mấu chốt là phân loại được biểu thức Toán học f(x) là được.

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Nếu các bạn chưa biết hoặc biết mà không chắc chắn thì hãy xem lại ngay cách phân loại các biểu thức Toán học nha các bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn