Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Hàm số bậc hai có dạng đầy đủ là $y=ax^2+bx+c$ với điều kiện $a \neq 0$.
Tuy nhiên, do giới hạn của chương trình Toán học Trung học cơ sở chưa học khái niệm Đạo hàm và việc vẽ đồ thị hàm số bậc hai ở dạng đầy đủ chỉ bằng các kiến thức của Đại số sơ cấp khá là phức tạp.
Vậy nên, thay vì hướng dẫn vẽ đồ thị của hàm số bậc hai ở dạng đầy đủ thì mình sẽ hướng dẫn cho các bạn cách vẽ với dạng thiếu là $y=ax^2$.
Có thể bạn đang tìm?
Cách vẽ đồ thị hàm số bậc nhất (trên giấy & trên máy tính)
Mục Lục Nội Dung
I. Sơ lược về đồ thị của hàm số bậc hai
Đồ thị của hàm số bậc hai $y=ax^2$ là một đường cong đi qua gốc tọa độ $O=(0; 0)$ và nhận trục tung $Oy$ làm trục đối xứng.
Vì đường cong này là một dạng đường cong thường gặp trong Toán học cũng như trong cuộc sống nên nó đã được đặt một tên riêng, gọi là Parabol.
- Trường hợp $a$ dương thì đồ thị nằm phía trên trục hoành $Ox$, lúc bấy giờ điểm thấp nhất của đồ thị là gốc tọa độ $O=(0; 0)$
- Trường hợp $a$ âm thì đồ thị nằm phía dưới trục hoành $Ox$, lúc bấy giờ điểm cao nhất của đồ thị là gốc tọa độ $O=(0; 0)$
II. Cách vẽ đồ thị của hàm số bậc 2 trên giấy
Nếu được, ngoài bút chì và thước thẳng ra thì bạn hãy chuẩn bị thêm thước Parabol để việc vẽ đồ thị được chính xác và nhanh chóng hơn nhé.
Đồ thị hàm số $y=ax^2$ luôn đi qua gốc tọa độ $O=(0; 0)$ và nhận trục tung $Oy$ làm trục đối xứng nên ta chỉ cần tìm 2 điểm ở bên phải hoặc ở bên trái trục tung $Oy$ rồi lấy thêm 2 điểm đối xứng
Bạn có thể lấy nhiều hơn 2 điểm hoặc lấy hai điểm theo cách khác nhưng mình thường lấy $A=(1; a)$ và $B=(2; 4a)$ => sau đó lấy đối xứng qua trục tung $Oy$ ta được $A’=(-1; a)$ và $B’=(-2; 4a)$
Cuối cùng bạn dùng thước Parabol để vẽ đường cong đi qua 5 điểm $A, B ,A’, B’$ và $O$ là xong.
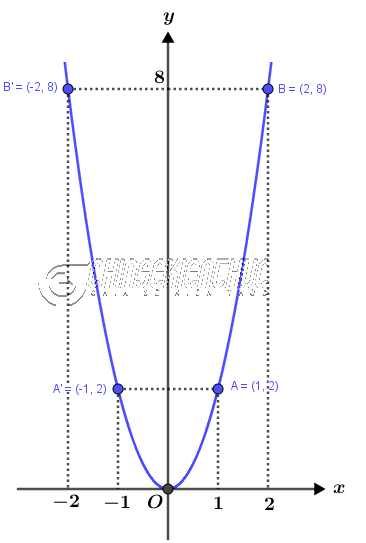
Ví dụ 1: Vẽ đồ thị của hàm số bậc hai $y=2x^2$
Dễ thấy điểm $A=(1; 2)$ và $B=(2; 8)$ thuộc đồ thị hàm số.
Lấy đối xứng qua trục tung $Oy$ ta được $A’=(-1; 2)$ và $B’=(-2; 8)$ cũng thuộc đồ thị hàm số.
Gốc tọa độ $O=(0; 0)$ dĩ nhiên thuộc đồ thị hàm số
=> Như vậy chúng ta đã có 5 điểm thuộc đồ thị hàm số là $A=(1; 2), B=(2; 8), A’=(-1; 2), B’=(-2; 8)$ và $O=(0; 0)$
Nhận xét về đồ thị:
Vẽ đồ thị hàm số là một trong những cách dễ nhất để minh họa các tính chất của hàm số.
Cụ thể trong trường hợp này là …
- Khi $x$ âm và tăng thì đồ thị của hàm số đi xuống.
- Khi $x$ dương và tăng thì đồ thị của hàm số đi lên.
Một số lưu ý khi vẽ:
- 5 điểm là vừa đủ để vẽ được đồ thị, 7 điểm sẽ hơi tốn thời gian, còn 3 điểm thì khó vẽ được chính xác.
- Bạn có thể tìm tọa độ điểm A và điểm B theo cách khác, miễn sao thuộc đồ thị hàm số là được
- Cho x bằng … suy ra $y=a …^2$ là cách tìm tọa độ của một điểm thuộc đồ thị hàm số nhanh nhất.
- Nếu giá trị tuyệt đối của $a$ là một số lớn thì nên cho $x$ một giá trị nhỏ và ngược lại.
III. Cách vẽ đồ thị của hàm số bậc hai trên máy tính
Trong bài viết này mình sẽ hướng dẫn các bạn cách vẽ đồ thị của hàm số bậc hai $y=ax^2$ bằngphần mềm GeoGebra 5.0 và bằng ứng dụng Caculator trên Windows 10, Windows 11..
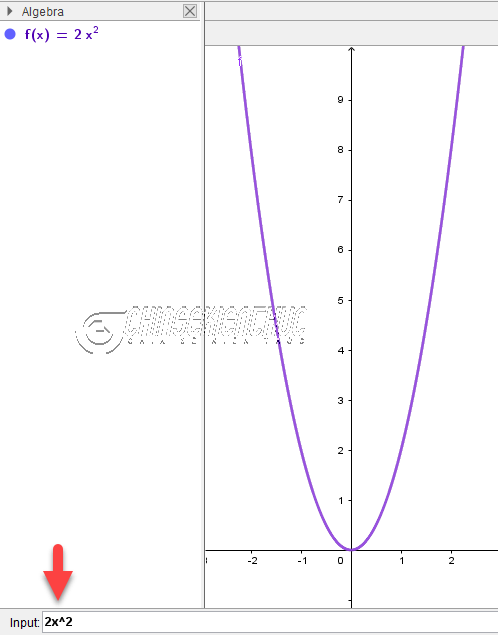
#1. Đối với phần mềm GeoGebra
Cách vẽ bằng phần mềm GeoGebra rất đơn giản, bạn chỉ cần nhập 2x^2 vào thanh nhập lệnh Input => sau đó nhấn phím Enter trên bàn phím là xong.
#2. Đối với ứng dụng Caculator
Bước 1. Nhấn tổ hợp phím Windows + R để mở hộp thoại Run => nhập từ khóa calc => nhấn phím Enter trên bàn phím để khởi động ứng dụng.
Cách mở Caculator này có thể áp dụng cho mọi phiên bản hệ điều hành Windows (7, 8, 10, 11….)
Đối với các hệ điều hành mới như Windows 10, Windows 11.. thì bạn có thể nhấn Windows + S => và tìm kiếm với từ khóa Caculator cũng được nhé.
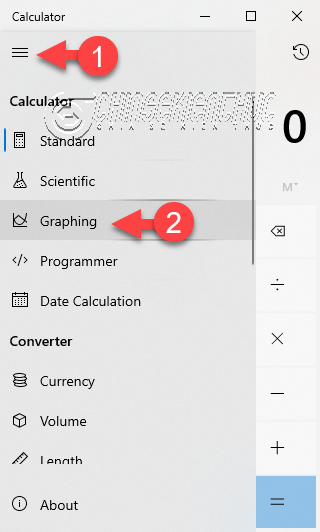
Bước 2. Chọn biểu tượng ≡ => chọn Graphing
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Bước 3. Chọn vào biểu tượng o để phóng to toàn bộ cửa sổ.
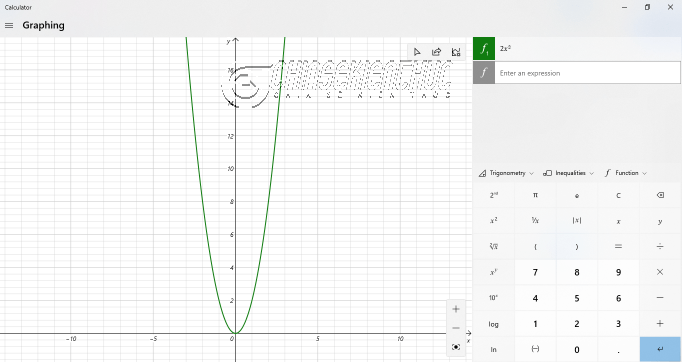
Bước 4. Nhập 2x^2 vào thanh lệnh Enter an expression => rồi nhấn phím Enter trên bàn phím.
Để xuất đồ thị ra thì bạn hãy nhấn chuột phải vào lưới tọa độ => chọn Copy => sau đó dán vào Word hoặc PowerPoint hoặc … đâu đấy, tùy theo nhu cầu của bạn.
Bạn cũng nên định dạng lại đồ thị cho phù hợp với yêu cầu của công việc trước khi xuất ra bạn nhé.
IV. Lời kết
Như vậy là mình đã hướng dẫn xong cho bạn cách vẽ đồ thị hàm số bậc 2 rồi nhé. Cũng rất đơn giản phải không nào !
Trước khi tạm ngừng bút thì mình xin có một gợi ý nhỏ nữa muốn gửi đến các bạn. Thay vì trình bày như trong bài viết thì bạn có thể trình bày tọa độ 5 điểm dưới dạng bảng (ở trường vẫn hay áp dụng).
Mặc dù trình bày theo cách này tuy không chuyên nghiệp nhưng nó Sư phạm, dễ tiếp cận với các bạn mới làm quen, các bạn hay bị sai sót khi tính toán. Okay. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
