Cách vẽ đồ thị hàm số bậc nhất (trên giấy & trên máy tính)

Như các bạn biết rồi đấy, đồ thị của hàm số bậc nhất là một trong những đồ thị thường gặp nhất trong Toán học.

Đồ thị của hàm số bắt đầu xuất hiện từ Trung học cơ sở cho đến Trung học Phổ thông và cả Đại học.

Vậy nên hôm nay chúng ta sẽ cùng nhau tìm hiểu về cách vẽ đồ thị của hàm số bậc nhất trên giấy và trên cả trên máy tính nữa nhé.

Việc tìm hiểu cách vẽ trên máy tính sẽ mang lại cho chúng ta nhiều lợi ích, tiêu biểu nhất là …

• Đối với học sinh thì để kiểm tra lại kết quả.
• Còn đối với giáo viên thì nó sẽ hỗ trợ công việc soạn giáo án điện tử, soạn để kiểm tra/ thi cử.

Okay, ngay bây giờ chúng ta hãy cùng nhau đi vào phần nội dung chi tiết nhé  …

I. Tìm hiểu về đồ thị của hàm số bậc nhất

Đồ thị hàm số $y=ax+b$ với điều kiện $a \neq 0$ là một đường thẳng.

Trong đó, đường thẳng này …

• Cắt trục tung $Oy$ tại điểm có tung độ bằng $b$
• Song song với đường thẳng $y=ax$ nếu $b \neq 0$
• Trùng với đường thẳng $y=ax$ nếu $b=0$

Đồ thị của hàm số $y=ax+b$ còn được gọi là đường thẳng $y=ax+b$, lúc bấy giờ $b$ được gọi là tung độ gốc.

II. Cách vẽ đồ thị hàm số bậc nhất trên giấy

Để thuận tiện cho các bạn theo dõi và thực hành mình đã chia thành hai trường hợp là $b=0$ và $b \neq 0$

#1. Trường hợp thứ 1: b=0

Khi $b=0$ thì hàm số $y=ax+b$ sẽ trở thành hàm số $y=ax$

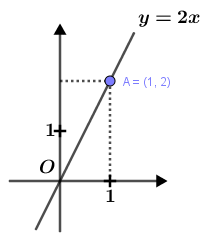
Lúc bấy giờ đồ thị của hàm số $y=ax$ chính là đường thẳng đi qua gốc tọa độ $O=(0; 0)$ và điểm $A=(1; a)$

Ví dụ 1: Vẽ đồ thị hàm số $y=2x$

Dễ thấy tọa độ của điểm $A=(1; 2)$

Đồ thị của hàm số $y=2x$ là một đường thẳng đi qua gốc tọa độ $O=(0; 0)$ và điểm $A=(1; 2)$

#2. Trường hợp thứ 2: $b \neq 0$

Chúng ta đã biết đồ thị của hàm số $y=ax+b$ là một đường thẳng.

Như vậy, muốn vẽ được đồ thị của hàm số này chúng ta cần xác định được tọa độ của hai điểm phân biệt thuộc đồ thị hàm.

Có rất nhiều cách để xác định tọa độ hai điểm thuộc đồ thị hàm số, tuy nhiên, để đơn giản thì chúng ta sẽ chọn giao của đồ thị hàm số với hai trục tọa độ.

• Giao điểm với trục tung $M=(0; b)$
• Giao điểm với trục hoành $N=(-\frac{b}{a}; 0)$

Vẽ đường thẳng đi qua hai điểm $M, N$ ta được đồ thị của hàm số $y=ax+b$

Chú ý:

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

• Trường hợp thứ nhất chính là trường hợp đặc biệt của trường hợp này tức bạn có thể áp dụng cách vẽ được chỉ dẫn trong trường hợp này để vẽ đồ thị hàm số $y=ax$
• Đồ thị hàm số $y=ax+b$ đi qua vô số điểm khác nhau

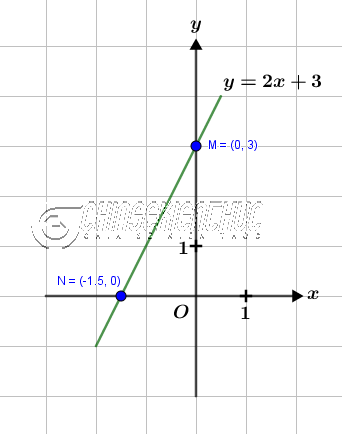
Ví dụ 2: Vẽ đồ thị của hàm số $y=2x+3$

Để thấy điểm $M=(0; 3)$, điểm $N=(\frac{-3}{2}; 0)$ thuộc đồ thị hàm số.

Đồ thị của hàm số $y=2x+$ là một đường thẳng đi qua điểm $M=(0; 3)$ và điểm $N=(\frac{-3}{2}; 0)$

III. Cách vẽ đồ thị hàm số trên máy tính

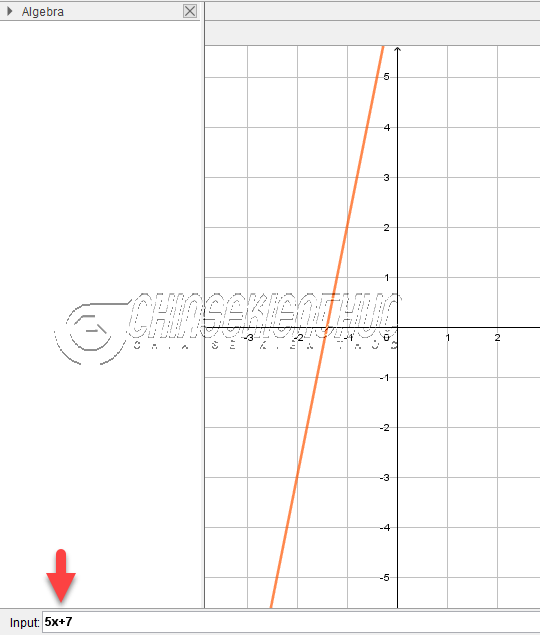
Ví dụ 3: Vẽ đồ thị của hàm số $y=5x+7$

Bước 1: Nháy đúp chuột vào biểu tượng  trên màn hình nền để khởi động phần mềm lên.

Bước 2: Nhập $5x+7$ vào thanh Input => nhấn phím Enter trên bàn phím

Sau khi vẽ xong, nếu cần thì bạn có thể xuất file. Nhưng trước đó thì bạn nên …

• Tùy chỉnh / định dạng lại hệ trục tọa độ, lưới, đồ thị, … sao cho phù hợp với nhu cầu cụ thể.
• Nhấn, giữ và kéo thả chuột phải để tạo vùng chọn => nhấn tổ hợp phím Ctrl + Shift + C để sao chép vùng chọn vào bộ nhớ đệm => khởi động ứng dụng Word hoặc PowerPoint… lên => nhấn tổ hợp phím Ctrl + V để dán vào

IV. Lời kết

Vâng, như vậy là trong bài viết này mình đã chia sẻ cho các bạn 2 cách vẽ đồ thị hàm số bậc nhất theo cách “truyền thống” và trên cả máy tính rồi nhé !

Tuy cách làm ở trường hợp thứ  2 có thể vẽ được đồ thị ở trường hợp thứ 1 nhưng khi hàm số được cho dưới dạng đặc biệt, ví dụ như là $y=ax$ thì bạn nên áp dụng theo cách đặc biệt.

Đó mới là phương án tối ưu nhất, giúp bạn tiết kiệm được nhiều thời gian, công sức và có tính sư phạm hơn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com