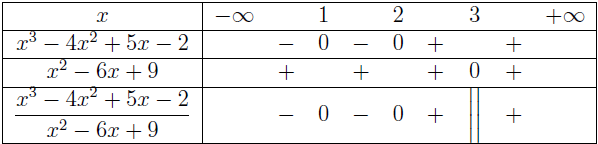Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Trong nội dung bài viết này, mình sẽ hướng dẫn các bạn cách xét dấu một biểu thức hữu tỉ (phân thức) bất kỳ.
Việc xét dấu một biểu thức hữu tỉ (phân thức) có nhiều giá trị trong Toán học, ví dụ như:
Mục Lục Nội Dung
#1. Biểu thức hữu tỉ (phân thức) có dạng như thế nào?
Biểu thức có dạng $\frac{P(x)}{Q(x)}$ với $P(x)$ và $Q(x)$ là những đa thức được gọi là biểu thức hữu tỉ (phân thức).
$f(x)=\frac{x^3-6 x^2+11 x-6}{x^2-9 x+20}, g(x)=\frac{x^3-4 x^2+5 x-2}{x^2-6 x+9}$ là những biểu thức hữu tỉ (phân thức)
#2. Các bước xét dấu biểu thức hữu tỉ
Bước 1. Tìm nghiệm của tử thức và mẫu thức.
Bạn có thể xem chúng là phương trình đa thức rồi tiến hành giải bằng các kiến thức đã có hoặc sử dụng máy tính cầm tay Casio.
Xem thêm cách giải phương trình bậc hai một ẩn, bậc ba một ẩn, bậc bốn một ẩn
Bước 2. Sắp xếp các nghiệm vừa tìm được theo thứ tự tăng dần.
Bước 3. Lập bảng xét dấu rồi tiến hành xét dấu tử thức và mẫu thức rồi suy ra dấu của biểu thức hữu tỉ.
- Khoảng cuối cùng dấu với hệ số $a$
- Qua nghiệm đơn và nghiệm bội lẻ đổi dấu
- Qua nghiệm kép và nghiệm bội chẵn không đổi dấu
#3. Bài tập xét dấu biểu thức hữu tỉ
Ví dụ 1. Xét dấu biểu thức hữu tỉ $f(x)=\frac{x^3-6 x^2+11 x-6}{x^2-9 x+20}$
Lời giải:
Đặt
- $P(x)=x^3-6 x^2+11 x-6$
- $Q(x)=x^2-9 x+20$
Vì tổng các hệ số của $P(x)=0$ nên $P(x)$ có một nghiệm là $1$
Chia $x^3-6 x^2+11 x-6$ cho $x-1$ chúng ta được $x^2-5x+6$
=> $P(x)$ $=x^3-6 x^2+11 x-6$ $=(x-1)(x^2-5x+6)$ $=(x-1)(x-2)(x-3)$
Vậy $P(x)$ có ba nghiệm đơn là $1, 2, 3$
Dễ thấy $Q(x)=x^2-9 x+20=(x-4)(x-5)$
Vậy $Q(x)$ có hai nghiệm đơn là $4, 5$
+) Lập bảng xét dấu
Gợi ý [phần này không trình bày vào lời giải nha các bạn]
- Kẻ bảng
- Điền tử thức, mẫu thức và biểu thức hữu tỉ vào cột đầu tiên.
- Điền các nghiệm của tử thức và mẫu thức theo thứ tự tăng dần vào dòng đầu tiên.
- Dòng thứ 2 tương ứng với các nghiệm của tử thức chúng ta viết số $0$
- Dòng thứ 3 tương ứng với các nhiệm của mẫu thức chúng ta viết số $0$
- Dòng cuối cùng tương ứng với các nghiệm của tử thức chúng ta viết số $0$ và tương ứng các nhiệm của mẫu thức chúng ta viết ký tự ||
+) Xét dấu tử thức
Khoảng cuối tức khoảng $(3, +\infty)$ cùng dấu với hệ số $a$ tức dấu cộng
=> $(3, +\infty)$ mang dấu cộng
Các nghiệm $1, 2, 3$ đều là nghiệm đơn nên trên khoảng $(2, 3)$ mang dấu trừ, $(1, 2)$ mang dấu cộng và $(-\infty, 1)$ mang dấu trừ
+) Xét dấu mẫu thức
Khoảng cuối tức khoảng $(5, +\infty)$ cùng dấu với hệ số $a$ tức dấu cộng.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
=> $(5, +\infty)$ mang dấu cộng.
Các nghiệm $4, 5$ đều là nghiệm đơn nên trên khoảng $(4, 5)$ mang dấu trừ, $(-\infty, 4)$ mang dấu cộng.
+) Xét dấu biểu thức hữu tỉ
Gợi ý [phần này không trình bày vào lời giải các bạn nhé]
Chúng ta sẽ xét dấu biểu thức hữu tỉ nhờ dấu của tử thức và mẫu thức
- “Cộng chia cộng hoặc trừ chia trừ bằng cộng”
- “Cộng chia trừ hoặc trừ chia cộng bằng trừ”
Vậy $f(x)$ nhận giá trị …
- Dương trên khoảng $(1, 2)$ và $(3, 4)$ và $(5, +\infty)$
- Âm trên khoảng $(-\infty, 1)$ và $(2, 3)$ và $(4, 5)$
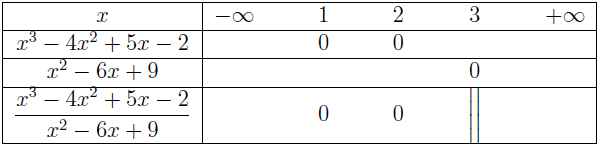
Ví dụ 2. Xét dấu biểu thức hữu tỉ $g(x)=\frac{x^3-4 x^2+5 x-2}{x^2-6 x+9}$
Lời giải:
Đặt
- $U(x)= x^3-4 x^2+5 x-2$
- $W(x)= x^2-6 x+9$
Vì tổng các hệ số của $U(x)=0$ nên $U(x)$ có một nghiệm là $1$
Chia $x^3-4 x^2+5 x-2$ cho $x-1$ chúng ta được $x^2-3x+2$
=> $U(x)$ $= x^3-4 x^2+5 x-2$ $=(x-1)( x^2-3x+2)$ $=(x-1)(x-1)(x-2)$
Vậy $U(x)$ có một nghiệm kép là $1$ và một nghiệm đơn là $2$
Dễ thấy $V(x)$ $= x^2-6 x+9$ $=(x-3)(x-3)$
Vậy $V(x)$ có một nghiệm kép là $3$
+) Lập bảng xét dấu
+) Xét dấu tử thức
Khoảng cuối tức khoảng $(2, +\infty)$ cùng dấu với hệ số $a$ tức dấu cộng
=> $(2, +\infty)$ mang dấu cộng
Vì $2$ là nghiệm đơn nên đổi dấu tức khoảng $(1, 2)$ mang dấu trừ
Vì $1$ là nghiệm kép nên không đổi dấu tức khoảng $(-\infty, 1)$ mang dấu trừ
+) Xét dấu mẫu thức
Khoảng cuối tức là khoảng $(3, +\infty)$ cùng dấu với hệ số $a$ tức dấu cộng
=> $(3, +\infty)$ mang dấu cộng
Vì $3$ là nghiệm kép nên không đổi dấu tức khoảng $(-\infty, 3)$ mang dấu cộng.
+) Xét dấu biểu thức hữu tỉ
Vậy $g(x)$ nhận giá trị:
- Dương trên khoảng $(2, 3)$ và $(3, +\infty)$
- Âm trên khoảng $(-\infty, 1)$ và $(1, 2)$
Xem thêm;
Cách lập bảng xét dấu tự động bằng phần mềm Geophar
#4. Lời kết
Okay, trên đây là cách xét dấu biểu thức hữu tỉ (phân thức) mà bạn nên nắm được.
Lưu ý là việc xác định nghiệm tìm được là nghiệm đơn, nghiệm kép, nghiệm bội lẻ, nghiệm bội chẵn rất quan trọng, nếu bạn xác định sai thì bảng xét dấu sẽ sai theo.
Trường hợp bạn không xác định được nghiệm đơn, nghiệm kép, nghiệm bội lẻ, nghiệm bội chẵn thì:
+) Hãy lấy một giá trị đại diện trong khoảng cách xét dấu.
+) Tính giá trị biểu thức hữu tỉ tại giá trị vừa lấy.
- Nếu giá trị của biểu thức hữu tỉ là một số âm thì dấu của khoảng đang xét là dấu trừ.
- Nếu giá trị của biểu thức hữu tỉ là một số dương thì dấu của khoảng đang xét là dấu cộng.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
