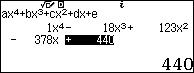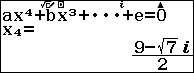2 cách giải phương trình bậc bốn và bài tập ví dụ

Vâng, sau khi tìm được cách giải phương trình bậc ba thì các nhà Toán học đã tiếp tục nghiên cứu và tìm ra cách giải phương trình bậc bốn.

Cụ thể là vào giữa thế kỉ thứ XVI thì nhà Toán học tài ba người Italia (Luđovicô Ferari) đã tìm ra cách giải tổng quát cho phương trình bậc bốn.

Hôm nay chúng ta sẽ cùng nhau ôn lại cách giải một số lớp phương trình bậc bốn thường gặp và tìm hiểu thêm cách giải phương trình bậc 4 bằng máy tính CASIO fx-580VN X, cũng như công cụ trực tuyến Wolfram Alpha.

I. Phương trình bậc bốn là gì?

Phương trình bậc bốn có dạng $ax^4+bx^3+cx^2+dx+e=0$ với $a, b, c, d, e$ là những số thực bất kì, $a$ khác $0$

Ví dụ. $x^4-18x^3+123x^2-378x+440=0$, $x^4-14x^3+71x^2-154x+117=0$, $-3x^4-2x^3+5x^2-2x-3=0$ là những phương trình bậc bốn.

II. Một số kiến thức cần ghi nhớ

• Nếu $a+b+c+d+e=0$ thì phương trình có nghiệm là $1$
• Nếu $a-b+c-d+e=0$ thì phương trình có nghiệm là $-1$
• Nếu phương trình có nghiệm nguyên thì chỉ có thể là một trong các ước của $e$
• Nếu phương trình có nghiệm hữu tỉ $\frac{p}{q}$ thì $p, q$ lần lượt theo thứ tự là các ước của $e$ và $a$
• Phương trình bậc bốn có tối đa bốn nghiệm

III.  Một số dạng đặc biệt thường gặp

#1. Phương trình trùng phương

Phương trình bậc bốn có dạng $ax^4+bx^2+c=0$ được gọi là phương trình trùng phương.

#2. Phương trình bậc bốn dạng $(x+a)^4+(x+b)^4=c$

Phương trình $(x+a)^4+(x+b)^4=c$ có thể chuyển về phương trình trùng phương bằng cách đặt ẩn phụ $y=x+\frac{a+b}{2}$

#3. Phương trình bậc bốn dạng $(x+a)(x+b)(x+c)(x+d)=m$ với $a+b=c+d$

Phương trình $(x+a)(x+b)(x+c)(x+d)=m$ với $a+b=c+d$ tương đương với $[x^2+(a+b)x+ab][x^2+(c+d)x+cd]=m$

Đặt $t=x^2+(a+b)x+ab$ chúng ta sẽ chuyển được phương trình đã cho thành phương trình bậc hai với ẩn $t$

#4. Phương trình đối xứng bậc bốn

Phương trình đối xứng bậc bốn là phương trình có dạng $ax^4+bx^3+cx^2+bx+a=0$

Bước 1. Kiểm tra $x=0$ có là nghiệm của phương trình hay không?

Bước 2. Nếu $x=0$ không là nghiệm của phương trình thì chia hai vế của phương trình cho $x^2$

$ax^{2}+b x+c+\frac{b}{x}+\frac{a}{x^{2}}=0 \Leftrightarrow a\left(x^{2}+\frac{1}{x^{2}}\right)+b\left(x+\frac{1}{x}\right)+c=0$

Đặt $t=x+\frac{1}{x} \Rightarrow x^{2}+\frac{1}{x^{2}}=t^{2}-2$, điều kiện $|t| \geq 2$

Lúc này phương trình $a\left(x^{2}+\frac{1}{x^{2}}\right)+b\left(x+\frac{1}{x}\right)+c=0$ trở thành $a(t^{2}-2)+bt+c=0$

IV. Bài tập ví dụ

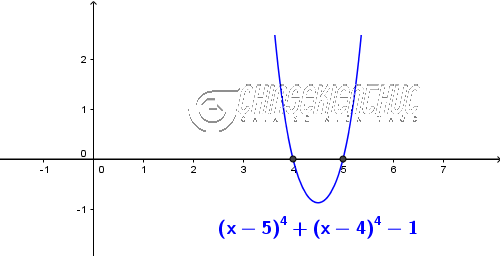
Ví dụ 1. Giải phương trình $(x-5)^4+(x-4)^4=1$

Cách 1. Đặt $y=x+\frac{(-5)+(-4)}{2}$

Đặt $y=x-\frac{9}{2}$ suy ra $x=y+\frac{9}{2}$

Phương trình trở thành $\left(y+\frac{9}{2}-5\right)^4+\left(y+\frac{9}{2}-4\right)^4-1=0$ $(*)$

$(*) \Leftrightarrow \left(y-\frac{1}{2}\right)^4+\left(y+\frac{1}{2}\right)^4-1=0 \Leftrightarrow 2y^4+3y^2-\frac{7}{8}=0$ $(**)$

Đặt $t=y^2$, điều kiện $t \geq 0$

Phương trình $(**)$ trở thành $2t^2+3t-\frac{7}{8}=0 \Leftrightarrow \left[\begin{array}{l} t=\frac{1}{4}\\ t=-\frac{7}{4}\end{array}\right. \Leftrightarrow t=\frac{1}{4}$

Với $t=\frac{1}{4}$ ta được phương trình $\frac{1}{4}=y^2 \Leftrightarrow y^2-\frac{1}{4}=0 \Leftrightarrow \left[\begin{array}{l} y=\frac{1}{2}\\ y=-\frac{1}{2}\end{array}\right.$

• Với $y=\frac{1}{2}$ ta được phương trình $x=\frac{1}{2}+\frac{9}{2}=5$
• Với $y=-\frac{1}{2}$ ta được phương trình $x=-\frac{1}{2}+\frac{9}{2}=4$

Vậy tập nghiệm của phương trình đã cho là $\{5, 4\}$

Cách 2. Tìm nghiệm nguyên

$(x-5)^4+(x-4)^4=1$ $(*)$

$(*) \Leftrightarrow 2x^4-36x^3+246x^2-756x+880=0 \Leftrightarrow x^4-18x^3+123x^2-378x+440=0$

$\pm 1, \pm 2, \pm 4, \pm 5, \pm 8, \pm 10, \pm 11, \pm 20, \pm 22, \pm 40, \pm 44, \pm 55, \pm 88, \pm 110, \pm 220, \pm 440$ là các ước của $440$

Lần lượt thay các ước trên vào vế trái của phương trình, ước nào làm cho vế trái bằng $0$ thì đó chính là nghiệm

$(1-5)^4+(1-4)^4 \neq 1$

$(2-5)^4+(2-4)^4 \neq 1$

$(4-5)^4+(4-4)^4=1$

$(5-5)^4+(5-4)^4=1$

Vì $4, 5$ là nghiệm của phương trình nên $(*) \Leftrightarrow (x-4)(x-5)(x^2-9x+22)=0$

Dễ thấy $(x^2-9x+22)=\left(x-\frac{9}{2}\right)^2+\frac{7}{4}>0$

Vậy tập nghiệm của phương trình đã cho là $\{5, 4\}$

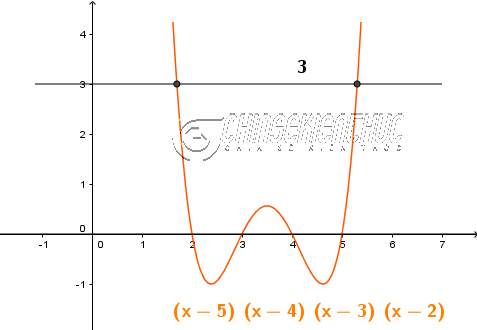
Ví dụ 2. Giải phương trình $(x-5)(x-4)(x-3)(x-2)=3$

Lời giải:

Phương trình $(x-5)(x-4)(x-3)(x-2)=3 \Leftrightarrow (x-5)(x-2)(x-4)(x-3)=3$ $(*)$

Phương trình $(*)$ có $(-5)+(-2)=(-4)+(-3)$

$(*) \Leftrightarrow (x^2-7x+10)(x^2-7x+12)=3$ $(**)$

Đặt $t=x^2-7x+10$ phương trình $(**)$ trở thành $(t)(t+2)=3 \Leftrightarrow t^2+2t-3=0 \Leftrightarrow \left[\begin{array}{l} t=1 \\ t=-3\end{array}\right.$

Với $t=1$ ta được phương trình $1=x^2-7x+10 \Leftrightarrow x^2-7x+9=0 \Leftrightarrow \left[\begin{array}{l} x=\frac{7+\sqrt{13}}{2} \\ x=\frac{7-\sqrt{13}}{2}\end{array}\right.$

Với $t=-3$ ta được phương trình $-3=x^2-7x+10 \Leftrightarrow x^2-7x+13=0$

Vì $x^2-7x+13=(x-\frac{7}{2})^2+\frac{3}{4}>0$ nên phương trình vô nghiệm

Vậy tập nghiệm của phương trình đã cho là $\left\{\frac{7+\sqrt{13}}{2}, \frac{7-\sqrt{13}}{2}\right\}$

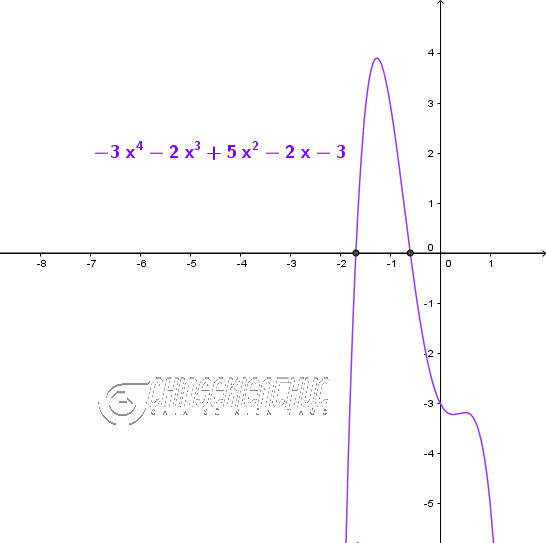
Ví dụ 3. Giải phương trình $-3x^4-2x^3+5x^2-2x-3=0$

Lời giải:

Dễ thấy $x=0$ không là nghiệm của phương trình.

Chia hai về của phương trình cho $x^2$ ta được $-3x^2-\frac{3}{x^2}-2x-\frac{2}{x}+5=0 \Leftrightarrow -3\left(x^2+\frac{1}{x^2}\right)-2\left(x+\frac{1}{x}\right)+5=0~(*)$

Đặt $t=x+\frac{1}{x} \Rightarrow x^{2}+\frac{1}{x^{2}}=t^{2}-2$, điều kiện $|t| \geq 2$

Lúc bấy giờ phương trình $(*)$ trở thành $-3(t^2-2)-2(t)+5=0 \Leftrightarrow -3t^2-2t+11=0 \Leftrightarrow\left[\begin{array}{l} t=\frac{-1+\sqrt{34}}{3} \\ t=\frac{-1-\sqrt{34}}{3}\end{array}\right.$

$t=\frac{-1+\sqrt{34}}{3}$ bị loại vì không thỏa mãn điều kiện $|t| \geq 2$

Với $\frac{-1-\sqrt{34}}{3}$ ta được phương trình $\frac{-1-\sqrt{34}}{3}=x+\frac{1}{x}$ $(**)$

$(**) \Leftrightarrow x+ \frac{1}{x}-\left(\frac{-1-\sqrt{34}}{3}\right)=0 \Leftrightarrow x^2+1-\left(\frac{-1-\sqrt{34}}{3}\right)x=0 \Leftrightarrow\left[\begin{array}{l} x=\frac{1}{6}\left(-1-\sqrt{34}-\sqrt{2\sqrt{34}-1}\right) \\ x=\frac{1}{6}\left(-1-\sqrt{34}+\sqrt{2\sqrt{34}-1}\right)\end{array}\right.$

V. Giải bằng máy tính CASIO fx-580VN X

Ở đây mình sẽ giải phương trình $x^4-18x^3+123x^2-378x+440=0$ trên máy tính CASIO fx-580VN X

Bước 1. Lần lượt nhấn các phím để chọn phương trình bậc 4.

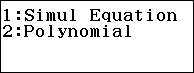
Bước 2. Lần lượt nhấn các phím  để nhập các hệ số $1, -18,  123, -378, 440$

Bước 3. Nhấn phím  để xem kết quả

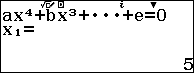
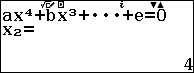
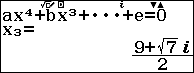
Chú ý:
Nghiệm $x_3$ và $x_4$ là nghiệm phức, nếu bạn là học sinh lớp 11 trở xuống thì vẫn kết luận tập nghiệm của phương trình đã cho là $\{5, 4\}$

VI. Giải bằng công cụ trực tuyến Wolfram Alpha

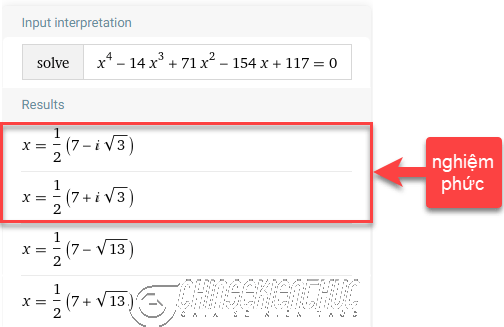
Ở đây mình sẽ giải phương trình $x^4-14x^3+71x^2-154x+117=0$ trên máy tính thông qua trình duyệt Google Chrome.

Bước 1. Truy cập vào trang chủ của dịch vụ trực tuyến Wolfram Alpha theo địa chỉ https://www.wolframalpha.com/

Bước 2. Nhập lệnh solve x^4-14x^3+71x^2-154x+117=0

Bước 3. Nhấn phím Enter trên bàn phím để xem kết quả:

Vậy tập nghiệm của phương trình đã cho là $\left\{\frac{7+\sqrt{13}}{2}, \frac{7-\sqrt{13}}{2}\right\}$

VII. Lời kết

Trong thực hành, khi được yêu cầu giải phương trình bậc bốn bất kỳ thì mình sẽ thực hiện lần lượt các bước bên dưới … (nếu ở Bước $n$ đã giải được phương trình thì không cần thực hiện Bước $n+1$ nữa nha các bạn).

• Bước 1. Quan sát xem phương trình có rơi vào các dạng đặc biệt hay không, nếu áp dụng phương pháp tương ứng để giải.
• Bước 2. Kiểm tra xem phương trình có nghiệm nguyên hoặc nguyên hữu tỉ hay không, nếu có thì tiến hành chia sơ đồ Hoocne để tìm phương trình bậc ba, bậc hai.
• Bước 3. Cố gắng phân tích phương trình đã cho thành phương trình tích
• Bước 4. Áp dụng thuật giải tổng quát của Italia Luđovicô Ferari

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn