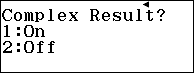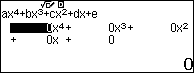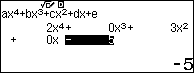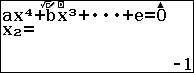Như các bạn đã biết, phương pháp tổng quát (nói chung) có thể áp dụng được cho mọi trường hợp nhưng thường khá là dài dòng, phương pháp đặc biệt thì ngược lại, tuy chỉ có thể áp dụng cho một số trường hợp cụ thể nhưng thường khá ngắn gọn.
Trong khi đó, phương trình trùng phương là một phương trình bậc bốn đặc biệt, vì vậy chúng ta nên áp dụng phương pháp đặc biệt để giải loại phương trình này thay vì áp dụng phương pháp tổng quát do Lodovico Ferrari đề xuất.
Chú ý:
Do đối tượng chủ yếu của bài viết này là học sinh Trung học cơ sở nên mình không trình bày nghiệm phức của phương trình nha các bạn.
Mục Lục Nội Dung
#1. Phương trình trùng phương có dạng như thế nào?
Phương trình trùng phương là phương trình có dạng $ax^4+bx^2+c=0$ với $a \neq 0$
Ví dụ. $2x^4+3x^2-5=0, 3x^4+5x^2=0, 5x^4+7=0$ là những phương trình trùng phương
ĐỊNH NGHĨA KHÁC:
Ngoài cách định nghĩa trên chúng ta có thể định nghĩa phương trình trùng phương như sau: Phương trình trùng phương là phương trình bậc bốn có hệ số đứng trước $x^3$ và $x$ là $0$
#2. Các bước giải phương trình trùng phương
Bằng cách đặt ẩn phụ thích hợp chúng ta có thể chuyển phương trình bậc bốn thành phương trình bậc hai tương ứng.
Nếu làm được như vậy thì việc giải phương trình trùng phương sẽ đơn giản hơn rất nhiều.
Trước hết, chúng ta đều thừa nhận mọi phương trình $ax^4+bx^2+c=0$ đều có thể viết dưới dạng $a(x^2)^2+b(x^2)+c=0$
Bước 1. Đặt $t=x^2$, điều kiện là $t \geq 0$
Bước 2.
- Lúc bấy giờ phương trình đã cho trở thành phương trình bậc hai $at^2+bt+c=0$, với ẩn
t. - Giải phương trình bậc hai vừa tìm được.
Bước 3. So sánh các nghiệm của phương trình $at^2+bt+c=0$ với điều kiện $t \geq 0$, nếu thỏa mãn thì thực hiện giải phương trình bậc hai với ẩn x
Bước 4. Kết luận tập nghiệm.
#3. Bài tập ví dụ về phương trình trùng phương
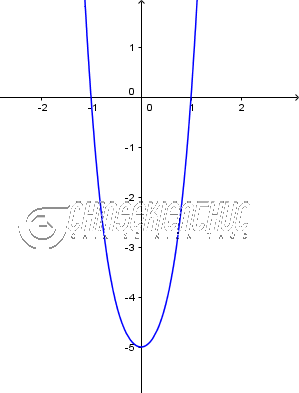
Ví dụ 1. Giải phương trình $2x^4+3x^2-5=0$
Lời giải:
Đặt $t=x^2$, điều kiện $t \geq 0$ ta được phương trình bậc hai, với ẩn t là $2t^2+3t-5=0$
Giải phương trình bậc hai $2t^2+3t-5=0$ ta được hai nghiệm là $t=1, t=-\frac{5}{2}$
$t=-\frac{5}{2}$ không thỏa điều kiện $t \geq 0$ nên bị loại
Với $t=1$ ta được $1=x^2$
Giải phương trình bậc hai $x^2=1$ ta được hai nghiệm là $1, -1$
Vậy nghiệm của phương trình đã cho là $1, -1$
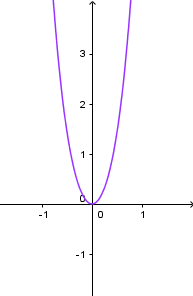
Ví dụ 2. Giải phương trình $3x^4+5x^2=0$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Lời giải:
Cách 1. Sử dụng thuật giải phương trình trùng phương
Đặt $t=x^2$, điều kiện $t \geq 0$ ta được phương trình bậc hai với ẩn t là $3t^2+5t=0$
Giải phương trình bậc hai $3t^2+5t=0$ ta được hai nghiệm là $t=-\frac{5}{3}, t=0$
$t=-\frac{5}{3}$ không thỏa điều kiện $t \geq 0$ nên bị loại
Với $t=0$ ta được $0=x^2$
Giải phương trình bậc hai $x^2=0$ ta được một kép nghiệm là $0$
Vậy nghiệm của phương trình đã cho là $0$
Cách 2. Đặt nhân tử chung
$3x^4+5x^2=0 \Leftrightarrow x^2(3x^2+5)=0 \Leftrightarrow x^2=0$ hoặc $3x^2+5=0$
- Phương trình $x^2=0$ có nghiệm kép là $x=0$
- Phương trình $3x^2+5=0$ vô nghiệm
Vậy nghiệm của phương trình đã cho là $0$
Ví dụ 3. Giải phương trình $5x^4+7=0$
Lời giải:
Cách 1. Sử dụng thuật giải phương trình trùng phương
Đặt $t=x^2$, điều kiện $t \geq 0$ ta được phương trình bậc hai với ẩn t là $5t^2+7=0$
Phương trình bậc hai $5t^2+7=0$ vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
Cách 2. Chứng minh vế trái của phương trình luôn lớn hơn 0
$5x^4+7=0 \Leftrightarrow x^4=-\frac{7}{5} \Leftrightarrow (x^2)^2=-\frac{7}{5}$ (vô lí)
Vậy phương trình đã cho vô nghiệm.
Chú ý:
$x^2$ không thể âm, tương tự $x^4$ cũng không thể âm.
#4. Giải phương trình trùng phương bằng máy tính CASIO
NOTE:
Đối với dòng máy tính CASIO được Bộ Giáo dục và Đào tạo cho phép mang vào phòng thi, tính đến thời điểm hiện tại chỉ có CASIO fx-580VN X là hỗ trợ giải phương trình trùng phương.
Giải sử mình cần giải phương trình $2x^4+3x^2-5=0$
Bước 1. Nhấn để cài đặt không hiển thị nghiệm phức

Chú ý:
Nếu không thực hiện bước này thì bạn cần tự loại thủ công nghiệm phức khi máy tính hiển thị.
Bước 2. Nhấn để chọn phương trình trùng phương.
Bước 3. Nhấn để nhập các hệ số $2, 0, 3, 0, -5$
Bước 4. Nhấn phím => nhấn phím
để xem kết quả
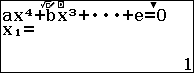
Chú ý:
- Hệ số đứng trước $x^3$ và $x$ đối với phương trình trùng phương luôn luôn bằng 0, tuy nhiên bạn vẫn phải nhập đầy đủ máy tính mới có thể tìm ra nghiệm chính xác.
- Máy tính CASIO fx-580VN X có thể giải được phương trình bậc bốn với các hệ số bất kì chứ không chỉ phương trình trùng phương.
#5. Lời kết
Bản chất của phương trình trùng phương chính là phương trình bậc bốn dạng đặc biệt, tuy nhiên dạng đặc biệt này rất thường gặp trong Toán học, vậy nên được đặc tên riêng là trùng phương.
Trong quá trình làm bài tập, nếu gặp một phương trình bậc bốn bất kỳ thì bạn hãy kiểm tra xem phương trình có rơi vào các trường hợp đặc biệt hay không, nếu có hãy áp dụng các phương pháp đặc biệt, nếu không có hãy áp dụng phương pháp tổng quát do Lodovico Ferrari đề xuất.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- 3 cách giải phương trình chứa dấu giá trị tuyệt đối
- Hướng dẫn cách giải phương trình chứa ẩn ở mẫu
- 2 cách giải phương trình vô tỉ (2 dạng thường gặp nhất)
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống