2 cách rút gọn phân thức đại số (có ví dụ dễ hiểu)

Rút gọn phân thức là một trong những thao tác thường gặp nhất khi tính toán với phân thức.

Chẳng hạn trước khi quy đồng thì bạn sẽ cần phải rút gọn, hoặc là trước và sau khi thực hiện các phép tính (cộng, trừ, nhân, chia) cũng cần phải rút gọn trước, …

Vậy cách rút gọn một phân thức đại số như thế nào? Có bao nhiêu bước? Có gì giống và khác với cách rút gọn phân số?

Đáp án cho ba câu hỏi trên đã được mình trình bày chi tiết ngay bên dưới đây, các bạn tham khảo và áp dụng nhé !

#1. Phân thức đại số là gì?

Biểu thức đại số có dạng $\frac{A(x)}{B(x)}$ với $A(x), B(x)$ là những đa thức và $B(x)$ khác 0 được gọi là phân thức (phân thức đại số).

Ví dụ. $\frac{2}{x}, \frac{3x+5}{7}, \frac{2x+3}{5x^2+7x+11}$ là những phân thức đại số.

Phân thức $\frac{2x+3}{5x^2+7x+11}$ có tử thức là đa thức $2x+3$ và mẫu thức là $5x^2+7x+11$.

Chú ý:

• Một phân số bất kỳ cũng được xem là một phân thức (một số nguyên khác 0 bất kỳ được xem là một đa thức bậc 0)
• Một đa thức bất kỳ cũng được xem là một phân thức (mẫu thức bằng 1).

#2. Các bước rút gọn phân thức 

Dựa vào tính chất: Nếu chia cả tử thức và mẫu thức của một phân thức cho một nhân tử chung khác 0 của chúng thì ta được một phân thức mới bằng phân thức đã cho chúng ta có thể rút gọn một phân thức bất kỳ theo các bước sau:

Bước 1. Lần lượt phân tích tử thức và mẫu thức thành nhân tử.

Bước 2. Xác định các nhân tử chung.

Bước 3. Lần lượt chia tử thức và mẫu thức cho tích các nhân tử chung vừa tìm được.

#3. Bài tập ví dụ về rút gọn phân thức

Ví dụ 1. Rút gọn phân thức $\frac{x^3-10x^2+31x-30}{x^2-9x+14}$

Đối với phân thức này bạn nên sử dụng máy tính CASIO để phân tích đa thức thành nhân tử $x^3-10x^2+31x-30$ và đa thức $x^2-9x+14$ thành nhân tử.

Lời giải:

Dễ thấy $x^3-10x^2+31x-30=(x-2)(x-3)(x-5)$ và $x^2-9x+14=(x-2)(x-7)$

Suy ra, nhân tử chung của tử thức và mẫu thức là $x-2$

Suy ra, $\frac{x^3-10x^2+31x-30}{x^2-9x+14}=\frac{(x-2)(x-3)(x-5)}{(x-2)(x-7)}=\frac{(x-3)(x-5)}{x-7}$

Vậy phân thức rút gọn của phân thức $\frac{x^3-10x^2+31x-30}{x^2-9x+14}$ là $\frac{(x-3)(x-5)}{x-7}$ hay $\frac{x^2-8x+15}{x-7}$

Ví dụ 2. Rút gọn phân thức $\frac{x^3-8}{x^2-4}$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Đối với phân thức này bạn nên sử dụng các hằng đẳng thức đáng nhớ để phân tích. Cụ thể là hằng đẳng thức $a^3-b^3=(a-b)(a^2+ab+b^2)$ và $a^2-b^2=(a+b)(a-b)$

Lời giải:

Dễ thấy $x^3-8=x^3-2^3=(x-2)(x^2+x.2+2^2)=(x-2)(x^2+2x+4)$ và $x^2-4=x^2-2^2=(x+2)(x-2)$

Suy ra, nhân tử chung của tử thức và mẫu thức là $x-2$

Suy ra, $\frac{x^3-8}{x^2-4}=\frac{(x-2)(x^2+2x+4)}{(x+2)(x-2)}=\frac{x^2+2x+4}{x+2}$

Vậy phân thức rút gọn của phân thức $\frac{x^3-8}{x^2-4}$ là $\frac{x^2+2x+4}{x+2}$

#4. Cách rút gọn một phân thức đại số bằng công cụ WolframAlpha

Giả sử mình cần rút gọn phân thức $\frac{x^3-10x^2+31x-30}{x^2-9x+14}$

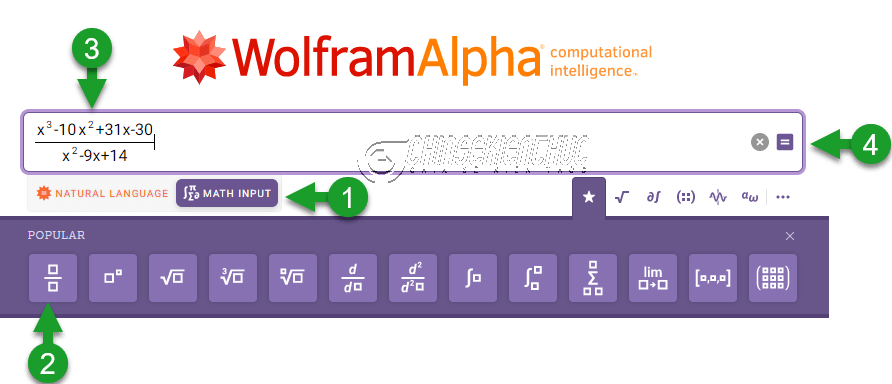
Bước 1. Bạn truy cập vào liên kết https://www.wolframalpha.com/ để truy cập đến trang chủ của công cụ WolframAlpha

Bước 2. Chọn MATH INPUT => chọn biểu tượng  => nhập tử thức và mẫu thức => chọn biểu tượng để xem kết quả.

Bước 3. Đọc kết quả:

Nếu không sử dụng lệnh chính xác mà chỉ nhập phân thức thì WolframAlpha sẽ tự động tính toán cho ra các kết quả của các bài toán thường gặp.

Chẳng hạn …

• Vẽ đồ thị
• Biểu diễn phân thức dưới các hình thức khác
• Nghiệm
• Tập xác định
• Miền xác định
• Khai triển chuỗi
• Đạo hàm
• Tích phân
• Giá trị lớn nhất, giá trị nhỏ nhất
• …

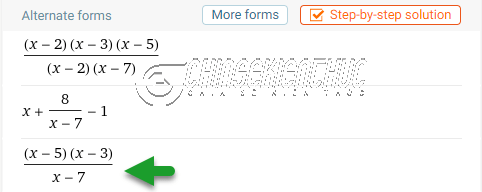
Ở đây chúng ta chỉ quan tâm đến việc rút gọn nên các bạn hãy chú ý vào dòng Alternate forms nha các bạn.

WolframAlpha đã tự động tính toán và biểu diễn phân thức $\frac{x^3-10x^2+31x-30}{x^2-9x+14}$ thành ba phân thức như hình bên trên. Ở đây phân thức thứ ba chính là phân thức rút gọn của phân thức đã cho.

Mình xin nói thêm một chút:

• Phân thức thứ nhất có tử thức và mẫu thức lần lượt là nhân tử của tử thức và mẫu thức của phân thức $\frac{x^3-10x^2+31x-30}{x^2-9x+14}$
• Phân thức thứ nhì thường được sử dụng khi cần tính tích phân của hàm số $f(x)=\frac{x^3-10x^2+31x-30}{x^2-9x+14}$
• Tất cả ba phân thức này đều bằng phân thức ban đầu.

#5. Lời kết

Việc rút gọn phân thức không có gì khó khăn cả, mấu chốt của dạng bài toán này là bạn phải phân tích được tử thức và mẫu thức thành nhân tử.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn