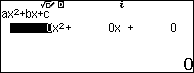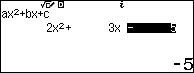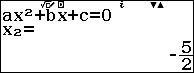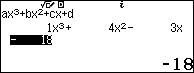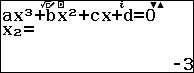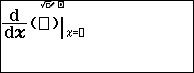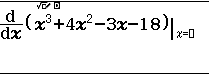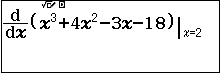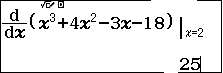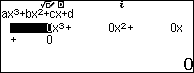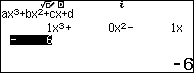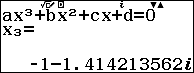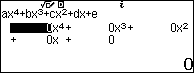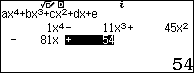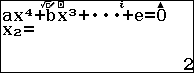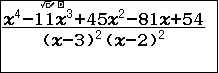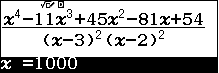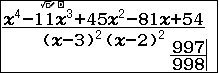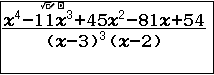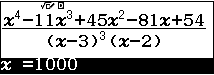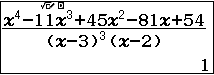Cách phân tích đa thức thành nhân tử bằng máy tính CASIO

Phân tích đa thức thành nhân tử là một trong những dạng bài toán rất thường gặp.

Thành thạo thủ thuật này sẽ giúp chúng ta dễ dàng trong việc rút gọn phân thức, giải phương trình tích, quy đồng mẫu thức nhiều phân thức, giải phương trình chứa ẩn ở mẫu, … rất nhiều bài tập sẽ được giải quyết một cách nhanh chóng hơn.

Đa thức nếu phân loại theo số lượng biến thì có hai loại, đó là: đa thức một biến và đa thức nhiều biến. Trong hai loại trên thì đa thức một biến là đa thức thường gặp nhất, cũng như là được ứng dụng nhiều nhất trong chương trình Toán học Trung học.

Vậy nên trong bài viết ngày hôm nay mình sẽ hướng dẫn các bạn thủ thuật phân tích nhanh đa thức một biến thành nhân tử bằng máy tính CASIO, để bạn có thể dễ dàng áp dụng vào việc giải bài tập ha.

#1. Đa thức một biến là gì?

Đa thức một biến là đa thức có dạng $a_0+a_1x+a_2x^2+\cdots+a_{n-2}x^{n-2}+a_{n-1}x^{n-1}+a_nx^n$, với $a_0, a_1, a_2, \dots a_n$ là những số thực cho trước và $n$ là một số nguyên dương:

Ví dụ.

• $2x^2+3x+5$ là đa thức một biến bậc hai.
• $2x^3-4x^2-6x-8$ là đa thức một biến bậc ba.
• $2x^4-3x^3+4x^2-5x+6$ là đa thức một biến bậc bốn.

#2. Một số chú ý

• Ở đây chúng ta sẽ tìm nghiệm của đa thức bằng cách giải phương trình tương ứng (nghiệm tìm được tương ứng với hệ số a bằng 1, nếu hệ số a của đa thức khác 1 thì bạn phải nhân thêm a).
• Nhất thiết phải xác định chính xác đâu là nghiệm đơn, nghiệm bội hai (nghiệm kép), nghiệm bội ba, …. Nếu xác định sai kết quả phân tích chắc chắn sẽ sai theo.

#3. Đa thức một biến bậc hai là gì?

Đa thức một biến bậc hai là đa thức có dạng $ax^2+bx+c$,  với a khác 0 và a, b, c là những số thực cho trước.

Lúc bấy giờ, đa thức $ax^2+bx+c=a(x-x_1)(x-x_2)$ với $x_1, x_2$ là nghiệm của đa thức $ax^2+bx+c$

Ví dụ 1. Phân tích đa thức $2x^2+3x-5$ thành nhân tử.

Bước 1. Nhấn để chọn phương trình bậc hai.

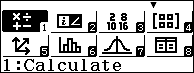
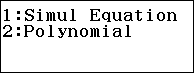
Bước 2. Nhấn  để nhập các hệ số 2, 3, -5

Bước 3. Nhấn  => nhấn  để tìm nghiệm

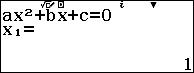
Suy ra $1, -\frac{5}{2}$ là nghiệm của đa thức $x^2+\frac{3}{2}x-\frac{5}{2}$

Vậy đa thức $2x^2+3x-5$ được phân tích thành nhân tử là $2(x-1)\left(x+\frac{5}{2}\right)$

#4. Đa thức một biến bậc ba

Đa thức một biến bậc ba là đa thức có dạng $ax^3+bx^2+cx+d$  với a khác 0 và a, b, c, d là những số thực cho trước.

Lúc bấy giờ đa thức $ax^3+bx^2+cx+d=a(x-x_1)(x-x_2)(x-x_3)$ với $x_1, x_2, x_3$ là nghiệm của đa thức $ax^3+bx^2+cx+d$

Ví dụ 2. Phân tích đa thức $x^3+4x^2-3x-18$ thành nhân tử.

Bước 1. Nhấn để chọn phương trình bậc ba.

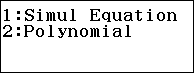
Bước 2. Nhấn  để nhập các hệ số 1, 4, -3, -18

Bước 3. Nhấn  => nhấn để tìm nghiệm.

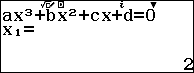
Suy ra $2, -3$ là nghiệm của đa thức $x^3+4x^2-3x-18$

Thủ thuật xác định nghiệm của đa thức một biến bậc ba là nghiệm đơn hay nghiệm kép

Bước 1. Nhấn để chọn phương thức tính toán Calculate.

Bước 2. Nhấn phím để chọn tính năng tính đạo hàm tại một điểm.

Bước 3. Nhấn  để nhập đa thức $x^3+4x^2-3x-18$

Bước 4. Nhấn  để nhập đạo hàm tại điểm 2

Bước 5. Nhấn  phím để xem kết quả

Kết quả khác 0. Vậy => 2 là nghiệm đơn và -3 sẽ là nghiệm kép, không tin bạn cứ thử với -3, kết quả chắc chắn sẽ bằng 0

Quay trở lại Ví dụ 2, lúc bấy giờ chúng ta đã xác định được $2, -3$ (nghiệm kép) là nghiệm của đa thức $x^3+4x^2-3x-18$

Vậy đa thức $x^3+4x^2-3x-18$ được phân tích thành nhân tử là $(x-2)(x+3)(x+3)$

Ví dụ 3. Phân tích đa thức $x^3-x-6$ thành nhân tử.

Bước 1. Nhấn để chọn phương trình bậc ba.

Bước 2. Nhấn  để nhập các hệ số 1, 0 -1, -6

Bước 3. Nhấn  => nhấn  => nhấn   để tìm nghiệm

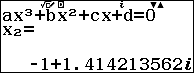
Suy ra $2$ là nghiệm thực và $-1+\sqrt{2}i, -1-\sqrt{2}i$ là nghiệm phức của đa thức $x^3-x-6$

Vậy $x^3-x-6=(x-2)\frac{x^3-x-6}{x-2}=(x-2)(x^2+2x+3)$

#5. Đa thức một biến bậc bốn là gì?

Đa thức một biến bậc bốn là đa thức có dạng $ax^4+bx^3+cx^2+dx+e$  với a khác 0 và a, b, c, d, e là những số thực cho trước.

Lúc bấy giờ, đa thức $ax^4+bx^3+cx^2+dx+e=a(x-x_1)(x-x_2)(x-x_3)(x-x_4)$ với $x_1, x_2, x_3, x_4$ là nghiệm của đa thức $ax^4+bx^3+cx^2+dx+e$

Ví dụ 4. Phân tích đa thức $x^4-11x^3+45x^2-81x+54$ thành nhân tử

Bước 1. Nhấn để chọn phương trình bậc bốn.

Bước 2. Nhấn  để nhập các hệ số 1, -11, 45, -81, 54

Bước 3. Nhấn => nhấn  để tìm nghiệm.

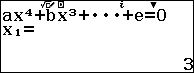
Suy ra $3, 2$ là nghiệm của đa thức $x^4-11x^3+45x^2-81x+54$

Cách kiểm tra nhanh bằng máy tính CASIO

+) Kiểm tra trường hợp 3 là nghiệm kép và 2 là nghiệm kép

Bước 1. Nhập phân thức $\frac{x^4-11x^3+45x^2-81x+54}{(x-3)^2(x-2)^2}$

Bước 2. Nhấn

Bước 3. Nhấn

Kết luận: Vì giá trị tìm được không là một số nguyên khác 0, vậy nên => trường hợp 3 là nghiệm kép và 2 là nghiệm kép không thể xảy ra.

+) Kiểm tra trường hợp 3 là nghiệm bội 3 và 2 là nghiệm đơn

Bước 1. Nhập phân thức $\frac{x^4-11x^3+45x^2-81x+54}{(x-3)^3(x-2)}$

Bước 2. Nhấn

Bước 3. Nhấn

Kết luận: Vì giá trị tìm được là 1 nên 3 là nghiệm bội 3 và 2 là nghiệm đơn

Vậy $x^4-11x^3+45x^2-81x+54=(x-3)(x-3)(x-3)(x-2)$

Ví dụ 5. Phân tích đa thức $x^4-10x^3+37x^2-60x+36$ thành nhân tử

Thực hiện tương tự như Ví dụ 4 tìm được 2 và 3 là nghiệm của đa thức $x^4-10x^3+37x^2-60x+36$, đồng thời xác định được 2 là nghiệm kép và 3 cũng là nghiệm kép.

Vậy => $x^4-10x^3+37x^2-60x+36=(x-3)(x-3)(x-2)(x-2)$

#6. Lời kết

Vâng, trên đây là cách phân tích đa thức thành nhân tử bằng máy tính CASIO mà bạn nên nắm được.

Trong bài viết này mình lựa chọn đa thức một biến bậc hai, bậc ba và bậc bốn là vì đây là một trong những đa thức một biến thường gặp nhất trong quá trình học tập và thi cử của các bạn.

Vậy trường hợp đa thức cần phân tích không rơi vào một trong ba trường hợp mình hướng dẫn ở trên thì phải phân tích như thế nào đây?

• Nếu vẫn là đa thức một biến thì bạn hãy kết hợp thêm tính năng SOLVE, TABLE, …để tìm nghiệm rồi phân tích tương tự.
• Nếu là đa thức nhiều biến thì bạn hãy sử dụng các phương pháp Toán học như đặt nhân tử chung, dùng hằng đẳng thức, nhóm hạng tử, tách hạng tử, … để phân tích.

Hi vọng là những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn