Cách giải bất phương trình bậc nhất hai ẩn (có VÍ DỤ)

Trong bài viết này mình sẽ hướng dẫn các bạn cách giải bất phương trình bậc nhất hai ẩn.

Để thuận tiện cho việc tiếp thu kiến thức mới thì đầu tiên, mình sẽ trình bày với các bạn về định nghĩa, tiếp theo là các bước giải và cuối cùng là bài tập ví dụ.

#1. Bất phương trình bậc nhất hai ẩn có dạng như thế nào?

Bất phương trình bậc nhất hai ẩn là bất phương trình có dạng $a x+b y+c<0$ hoặc $a x+b y+c>0$ hoặc $a x+b y+c \leq 0$ hoặc $a x+b y+c \geq 0$

Trong đó:

• $a, b$ và $c$ là những số thực cho trước
• $a$ và $b$ không đồng thời bằng $0$
• $x$ và $y$ là những ẩn số

Ví dụ. $2x+3y+5>0$, $9x-2y+4 \leq 0$ là những bất phương trình bậc nhất hai ẩn

#2. Cách giải bất phương trình bậc nhất hai ẩn

Trước hết, các bạn cần biết tập nghiệm của bất phương trình bậc nhất hai ẩn còn được gọi là miền nghiệm.

Để tìm miền nghiệm của bất phương trình $a x+b y+c<0$ chúng ta thực hiện tuần tự theo các bước bên dưới.

Bước 1. Vẽ đường thẳng $(d): a x+b y+c=0$ lên mặt phẳng tọa độ $Oxy$

Bước 2. Lấy một điểm $M\left(x_0 ; y_0\right)$ không thuộc $(d)$

Bước 3. Thay điểm $M\left(x_0 ; y_0\right)$ vào bất phương trình $a x+b y+c<0$

• Nếu $ax_0+by_0+c<0$ thì nửa mặt phẳng không kể bờ $(d)$ chứa điểm $M$ chính là miền nghiệm của bất phương trình đã cho.
• Nếu $ax_0+by_0+c>0$ thì nửa mặt phẳng không kể bờ $(d)$ không chứa điểm $M$ chính là miền nghiệm của bất phương trình đã cho.

Chú ý:

• Việc tìm miền nghiệm của bất phương trình $a x+b y+c>0$ hoàn toàn tương tự
• Việc tìm miền nghiệm của các bất phương trình $a x+b y+c \leq 0$ hoặc $a x+b y+c \geq 0$ cũng tương tự nhưng miền nghiệm là nửa mặt phẳng kể cả bờ $(d)$

#3. Bài tập giải bất phương trình bậc nhất hai ẩn

Ví dụ 1. Giải bất phương trình $2x+3y+5>0$

Lời giải:

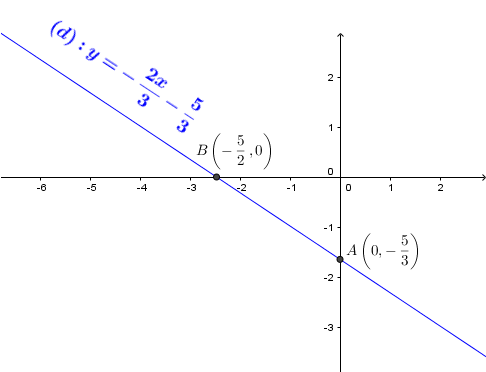
$(d): 2x+3y+5=0$ hoặc $(d): y=-\frac{2 x}{3}-\frac{5}{3}$

Để vẽ phương trình của đường thẳng $(d)$ lên mặt phẳng tọa độ $Oxy$ chúng ta cần tìm được ít nhất hai điểm thuộc $(d)$

Cho $x=0$ => $y=-\frac{5}{3}$

Cho $y=0$ => $x=-\frac{5}{2}$

Vậy hai điểm thuộc đường thẳng $(d)$ là $A\left(0, -\frac{5}{3}\right)$ và $B\left(-\frac{5}{2}, 0\right)$

Thay điểm $M(0, 0)$ không thuộc đường thẳng $(d)$ vào bất phương trình $2x+3y+5>0$ chúng ta được $2.0+3.0+5>0 \Leftrightarrow 5>0$

Vậy => điểm $M(0, 0)$ là một nghiệm của bất phương trình đã cho.

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

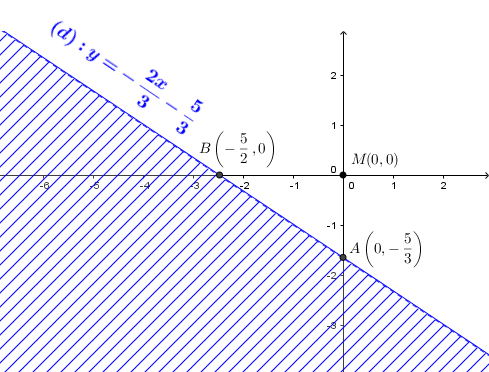
Vậy miền nghiệm của bất phương trình đã cho là nữa mặt phẳng chứa điểm $M(0, 0)$ và không bao gồm bờ của đường thẳng $(d)$

Miền nghiệm của bất phương trình $2x+3y+5>0$ là nữa mặt phẳng không bị gạch bỏ, không bao gồm bờ của đường thẳng $(d)$

Ví dụ 2. Giải bất phương trình $9x-2y+4 \leq 0$

Lời giải:

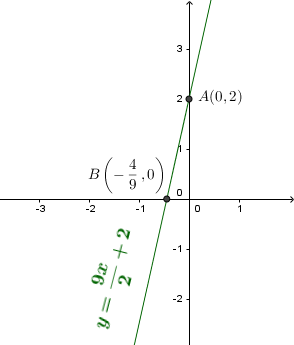
$(d): 9x-2y+4=0$ hoặc $(d): y=\frac{9x}{2}+2$

Để vẽ phương trình của đường thẳng $(d)$ lên mặt phẳng tọa độ $Oxy$ chúng ta cần được tìm được ít nhất hai điểm thuộc $(d)$

Cho $x=0$ => $y=2$

Cho $y=0$ => $x=-\frac{4}{9}$

Vậy hai điểm thuộc đường thẳng $(d)$ là $A(0, 2)$ và $B\left(-\frac{4}{9}, 0\right)$

Thay điểm $M(0, 0)$ không thuộc đường thẳng $(d)$ vào bất phương trình $9x-2y+4 \leq 0$ chúng ta được $9.0-2.0+4 \leq 0 \Leftrightarrow 4 \leq 0$ (vô lý)

Suy ra điểm $M(0, 0)$ là không nghiệm của bất phương trình đã cho

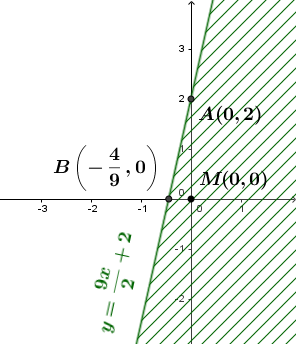
Vậy miền nghiệm của bất phương trình đã cho là nữa mặt phẳng không chứa điểm $M(0, 0)$ nhưng bao gồm bờ của đường thẳng $(d)$

Miền nghiệm của bất phương trình $9x-2y+4 \leq 0$ là nữa mặt phẳng không bị gạch bỏ và bờ của đường thẳng $(d)$

#4. Lời kết

Okay, như các bạn có thể thấy, việc giải bất phương trình bậc nhất 2 ẩn cũng không có gì quá khó khăn.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 2 cách giải bất phương trình bậc hai một ẩn, rất dễ
• 2 cách giải bất phương trình bậc nhất một ẩn (có ví dụ)
• Cách giải hệ bất phương trình bậc nhất một ẩn (có ví dụ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn