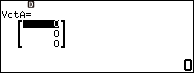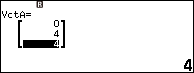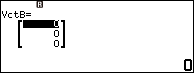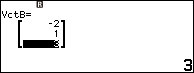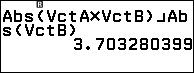Tính khoảng cách giữa điểm và đường thẳng bằng CASIO

Hôm nay mình sẽ hướng dẫn cho các bạn cách sử dụng tính năng tính toán véc tơ Vector của máy tính CASIO để tính nhanh khoảng cách giữa điểm và đường thẳng.

Điểm và đường thẳng được nhắc đến trong bài viết này là điểm và đường thẳng nằm trong không gian các bạn ha.

Việc tính khoảng cách giữa điểm và đường thẳng trên mặt phẳng rất đơn giản, chỉ cần áp dụng công thức là xong (công thức cũng rất dễ nhớ các bạn ạ).

#1. Tại sao mình giới thiệu thủ thuật này?

Tính khoảng cách giữa $M_1$ và (d), biết điểm $M_1=(x_1, y_1, z_1)$ và đường thẳng $(d): \frac{x-x_0}{p}=\frac{y-y_0}{q}=\frac{z-z_0}{r}$

Áp dụng công thức bên dưới chúng ta sẽ tính được khoảng cách giữa $M_1$ và (d):

$\frac{\sqrt{[(y_{1}-y_{0}).r-q.(z_{1}-z_{0})]^{2}+[(z_{1}-z_{0}).p-r(x_{1}-x_{0})]^{2}+[(x_{1}-x_{0}).q-p(y_{1}-y_{0})]^{2}}}{\sqrt{p^2+q^2+r^2}}$

Công thức bên trên khá phức tạp và cũng khá là khó nhớ, mặt khác, việc áp dụng trực tiếp cũng dễ dẫn đến sai sót.

Vâng, những khó khăn ở trên sẽ được khắc phục nhờ vào tính năng tính toán véc tơ Vector của máy tính CASIO.

#2. Các bước tính khoảng cách giữa điểm và đường thẳng bằng Casio

Các bước sử dụng máy tính CASIO để tính khoảng cách giữa điểm và đường thẳng trong không gian:

Ví dụ. Giả sử chúng ta cần tính khoảng cách giữa điểm $M_1=(x_1, y_1, z_1)$ và đường thẳng $(d): \frac{x-x_0}{p}=\frac{y-y_0}{q}=\frac{z-z_0}{r}$

Bước 1. Xác định điểm $M_0=(x_0, y_0, z_0)$ và véc tơ chỉ phương $\vec{u}=(p, q, r)$ của đường thẳng (d)

Bước 2. Xác định véc tơ $\overrightarrow{M_0M_1}$

Bước 3. Mở tính năng tính toán véc tơ Vector

Bước 4. Lần lượt gán véc tơ $\overrightarrow{M_0M_1}$ và $\vec{u}=(p, q, r)$ vào biến nhớ véc tơ VctA và VctB

Bước 5. Nhập công thức $\frac{Abs(VctA \times VctB)}{Abs(VctB)}$

#3. Cách tính khoảng cách giữa điểm và đường thẳng trên Casio fx 880 BTG

Ví dụ 1. Tính khoảng cách giữa điểm $M_1=(1, 5, 4)$ và đường thẳng $(d):\frac{x-1}{-2}=\frac{y-1}{1}=\frac{z}{3}$

Bước 1. Dễ thấy đường thẳng $(d)$ đi qua điểm $M_0=(1, 1, 0)$ và có véc tơ chỉ phương $\vec{u}=(-2, 1, 3)$

Bước 2. Dễ thấy véc tơ $\overrightarrow{M_0M_1}=(0, 4, 4)$

Bước 3. Mở tính năng tính toán véc tơ Vector

Nhấn phím HOME => chọn Vector => nhấn phím OK

Bước 4. Lần lượt gán véc tơ $\overrightarrow{M_0M_1}=(0, 4, 4)$ và $\vec{u}=(-2, 1, 3)$ vào biến nhớ véc tơ VctA và VctB

Bước 4.1. Gán véc tơ $\overrightarrow{M_0M_1}=(0, 4, 4)$ vào biến nhớ véc tơ VctA

Nhấn phím TOOLS => chọn VctA => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

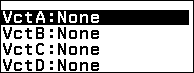
Nhập 0 => nhấn phím EXE => nhập 4 => nhấn phím EXE => nhập 4 => nhấn phím EXE

Nhấn phím EXE

Bước 4.2. Gán véc tơ $\vec{u}=(-2, 1, 3)$ vào biến nhớ véc tơ VctB

Nhấn phím TOOLS => chọn VctB => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

Nhập -2 => nhấn phím EXE => nhập 1 => nhấn phím EXE => nhập 3 => nhấn phím EXE

Nhấn phím EXE

Bước 5. Nhập công thức $\frac{Abs(VctA \times VctB)}{Abs(VctB)}$ => nhấn phím EXE

Vậy khoảng cách cần tìm gần bằng 3.703280399

Để hiển thị chính xác khoảng cách này chúng ta cần thực hiện thêm một số thao tác bên dưới.

Bước i. Nhấn phím HOME => chọn Calculate => nhấn phím OK

Bước ii. Nhập $\sqrt{Ans^2}$ => nhấn phím EXE

Vậy khoảng cách cần tìm bằng $\frac{4\sqrt{42}}{7}$

#4. Cách tính khoảng cách giữa điểm và đường thẳng trên Casio fx 580 VNX

Ví dụ 2. Tính khoảng cách giữa điểm $M_1=(1, 5, 4)$ và đường thẳng $(d):\frac{x-1}{-2}=\frac{y-1}{1}=\frac{z}{3}$

Bước 1. Dễ thấy đường thẳng $(d)$ đi qua điểm $M_0=(1, 1, 0)$ và có véc tơ chỉ phương $\vec{u}=(-2, 1, 3)$

Bước 2. Dễ thấy véc tơ $\overrightarrow{M_0M_1}=(0, 4, 4)$

Bước 3. Mở tính năng tính toán véc tơ Vector

Nhấn phím MENU => chọn Vector => nhấn phím = => nhấn phím AC

Bước 4. Lần lượt gán véc tơ $\overrightarrow{M_0M_1}=(0, 4, 4)$ và $\vec{u}=(-2, 1, 3)$ vào biến nhớ véc tơ VctA và VctB

Bước 4.1. Gán véc tơ $\overrightarrow{M_0M_1}=(0, 4, 4)$ vào biến nhớ véc tơ VctA

Nhấn phím OPTN => nhấn phím 1 => nhấn phím 1 => nhấn phím 3

Nhập 0 => nhấn phím = => nhập 4 => nhấn phím = => nhập 4 => nhấn phím =

Nhấn phím AC

Bước 4.2. Gán véc tơ $\vec{u}=(-2, 1, 3)$ vào biến nhớ véc tơ VctB

Nhấn phím OPTN => nhấn phím 1 => nhấn phím 2 => nhấn phím 3

Nhập –2 => nhấn phím = => nhập 1 => nhấn phím = => nhập 3 => nhấn phím =

Nhấn phím AC

Bước 5. Nhập công thức $\frac{Abs(VctA \times VctB)}{Abs(VctB)}$ => nhấn phím =

Vậy khoảng cách cần tìm gần bằng 3.703280399

Để hiển thị chính xác khoảng cách này chúng ta cần thực hiện thêm một số thao tác bên dưới.

Nhấn phím MENU => chọn Calculate => nhấn phím =

Nhập $\sqrt{Ans^2}$ => nhấn phím =

Vậy khoảng cách cần tìm bằng $\frac{4\sqrt{42}}{7}$

#5. Lời kết

Bằng cách sử dụng tính năng tính toán véc tơ và tính năng tính giá trị tuyệt đối Absolute Value của máy tính CASIO mà chúng ta đã tính được khoảng cách giữa điểm và đường thẳng một cách chính xác và nhanh chóng.

Mặc dù thao tác có hơi nhiều nhưng không hề khó nhớ các bạn nhé, nhiều thao tác lập đi lập lại nhiều lần, nếu quen tay thì việc thực hiện chỉ mất vài phút.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

Đọc thêm:

• Hướng dẫn 2 cách tính độ dài đường trung tuyến
• Cách tính véc tơ bằng máy tính Casio Fx 580 VNX
• Thực hiện các phép tính véc tơ bằng máy Casio Fx 880 BTG

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn