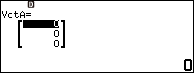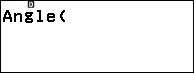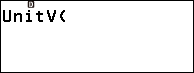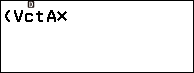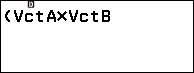Thực hiện các phép tính véc tơ bằng máy Casio Fx 880 BTG

I. Tính năng Vector trên máy tính Casio dùng để làm gì?

Tính năng Vector trên máy tính Casio là một công cụ cực kỳ mạnh mẽ để thực hiện các phép tính toán và phân tích về hình học vector trong không gian hai hoặc ba chiều.

Đây là một tính năng vô cùng quan trọng trên các máy tính khoa học và kỹ thuật của Casio, bao gồm cả các model điện tử và đồng hồ bấm giờ.

Các tính năng và chức năng của Vector trên máy tính Casio bao gồm:

1. Tính toán độ dài, phép cộng, phép trừ, phép nhân và phép chia của các vector.
2. Tính toán tích vô hướng và tích vector của hai vector.
3. Tính toán góc giữa hai vector và hệ số vectơ của một vector.
4. Tìm phương trình đường thẳng hoặc mặt phẳng đi qua các điểm đã cho.
5. Tìm điểm đối xứng của một điểm qua một đường thẳng hoặc một mặt phẳng.
6. Tìm hình chiếu của một vector lên một vector khác hoặc lên một mặt phẳng.

Các tính năng này rất hữu ích trong hình học vector, cơ học, vật lý, khoa học máy tính, và các lĩnh vực khác liên quan đến phép tính và phân tích về hình học vector.

Tính năng Vector của máy tính Casio Fx 880 BTG cho phép chúng ta gán tối đa 4 véc tơ vào 4 biến nhớ véc tơ rồi thực hiện các thao tác tính toán với các biến nhớ véc tơ vừa gán.

II. Cách thực hiện các phép tính véc tơ trên Casio Fx 880 BTG

NOTE:
Nếu chưa có máy tính Casio này thì bạn có thể đặt mua chính hãng tại đây hoặc tại đây !

Lần lượt gán $\vec{a}=(1, 8, 7), \vec{b}=(5, 0, 0)$ và $\vec{c}=(1, 8, 3)$ vào các biến nhớ véc tơ VctA, VctB và VctC rồi thực hiện theo các yêu cầu bên dưới:

1. a) Tính $\vec{a}+\vec{b}$
2. b) Tính độ dài $\vec{a}$
3. c) Tính tích vô hướng của $\vec{a}$ và $\vec{b}$
4. d) Tính tích có hướng của $\vec{a}$ và $\vec{b}$
5. e) Tính góc tạo bởi $\vec{a}$ và $\vec{b}$
6. f) Chuẩn hóa $\vec{a}$
7. g) Tích tích hỗn hợp (tích hỗn tạp) của $\vec{a}, \vec{b}$ và $\vec{c}$

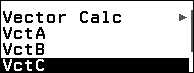
Bước 1. Nhấn phím HOME => chọn Vector => nhấn phím OK

Bước 2 Gán $\vec{a}=(1, 8, 7)$ vào biến nhớ véc tơ VctA

Nhấn phím TOOLS => chọn VctA => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK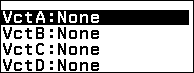

Nhập 1 => nhấn phím EXE => nhập 8 => nhấn phím EXE => nhập 7 => nhấn phím EXE

Nhấn phím EXE

Bước 3. Gán $\vec{b}=(5, 0, 0)$ vào biến nhớ véc tơ VctB

Nhấn phím TOOLS => chọn VctB => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

Nhập 5 => nhấn phím EXE => nhập 0 => nhấn phím EXE => nhập 0 => nhấn phím EXE

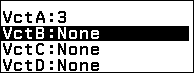
Nhấn phím EXE

Bước 4. Gán $\vec{c}=(1, 8, 3)$ vào biến nhớ véc tơ VctC

Nhấn phím TOOLS => chọn VctC => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

Nhập 1 => nhấn phím EXE => nhập 8 => nhấn phím EXE => nhập 3 => nhấn phím EXE

Nhấn phím EXE

#1. Tính tổng 2 vector $\vec{a}+\vec{b}$

Bước 1. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 2. Nhấn phím +

Bước 3. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctB => nhấn phím OK

Bước 4. Nhấn phím EXE

Vậy $\vec{a}+\vec{b}=(6, 8, 7)$

#2. Tính độ dài vector $\vec{a}$

Bước 1. Nhấn phím CATALOG => chọn Numeric Calc => nhấn phím OK => chọn Absolute Value => nhấn phím OK

Bước 2. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 3. Nhấn phím EXE

Bước 4. Nhấn phím  => nhấn phím EXE

Vậy độ dài của $\vec{a}$ là $\sqrt{114}$

#3. Tính tích vô hướng của 2 vector $\vec{a}$ và $\vec{b}$

Bước 1. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 2. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn Vector Calc => nhấn phím OK => chọn Dot Product => nhấn phím OK

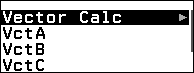
Bước 3. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctB => nhấn phím OK

Bước 4. Nhấn phím EXE

Vậy tích vô hướng của $\vec{a}$ và $\vec{b}$ là 5

#4. Tính tích có hướng của vector $\vec{a}$ và $\vec{b}$

Bước 1. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 2. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn Vector Calc => nhấn phím OK => chọn Cross Product => nhấn phím OK

Bước 3. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctB => nhấn phím OK

Bước 4. Nhấn phím EXE

Vậy tích có hướng của $\vec{a}$ và $\vec{b}$ là (0, 35, -40)

 

#5. Tính góc tạo bởi 2 vector $\vec{a}$ và $\vec{b}$

Bước 1. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn Vector Calc => nhấn phím OK => chọn Angle => nhấn phím OK

Bước 2. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 3. Nhấn phím SHIFT => nhấn phím )

Bước 4. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctB => nhấn phím OK

Bước 5. Nhấn phím EXE

Vậy góc tạo bởi hai véc tơ $\vec{a}$ và $\vec{b}$ gần bằng 1.477000275

#6. Chuẩn hóa véc tơ $\vec{a}$

Bước 1. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn Vector Calc => nhấn phím OK => chọn Unit Vector => nhấn phím OK

Bước 2. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 3. Nhấn phím EXE

Bước 4.

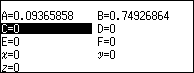
Bước 4.1. Chọn “hoành độ” => nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK

Bước 4.2. Chọn “trung độ” => nhấn phím VARIABLE => chọn biến nhớ B => nhấn phím OK => chọn Store => nhấn phím OK

Bước 4.3. Chọn “cao độ” => nhấn phím VARIABLE => chọn biến nhớ C => nhấn phím OK => chọn Store => nhấn phím OK

Bước 5. Nhấn phím HOME => chọn Calculate => nhấn phím OK

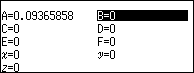
Bước 6.

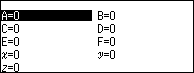
Bước 6.1. Nhập $A^2$ => nhấn phím EXE

Bước 6.2. Nhập $B^2$ => nhấn phím EXE

Bước 6.3. Nhập $C^2$ => nhấn phím EXE

Vậy véc tơ chuẩn hóa của $\vec{a}$ là $\left(\sqrt{\frac{1}{114}}, \sqrt{\frac{32}{57}}, \sqrt{\frac{49}{114}}\right)$

Chú ý: Độ dài của véc tơ sau khi chuẩn hóa luôn luôn bằng 1

#7. Tích tích hỗn hợp (tích hỗn tạp) của $\vec{a}, \vec{b}$ và $\vec{c}$

Bước 1. Nhấn phím ( => nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 2. Nhấn phím

Bước 3. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctB => nhấn phím OK => nhấn phím )

Bước 4. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn Vector Calc => nhấn phím OK => chọn Dot Product => nhấn phím OK

Bước 5. Nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctC => nhấn phím OK

Bước 6. Nhấn phím EXE

Vậy tích hỗn hợp của ba véc tơ $\vec{a}, \vec{b}$ và $\vec{c}$ là 160

III. Xem video cách tính vector bằng máy Casio Fx 880 BTG

IV. Lời kết

Trên đây là chi tiết các bước sử dụng tính năng Vector của máy tính Casio Fx 880 BTG để thực hiện các phép tính vector.

Việc sử dụng thành thạo tính năng này sẽ mang lại cho chúng ta khá nhiều lợi ích trong học tập, kiểm tra và thi cử.

Một số lợi ích tiêu biểu có thể kể đến như:

• Tính nhanh diện tích tam giác, diện tích hành bình hành khi biết tọa độ ba đỉnh.
• Viết phương trình đường phân giác của một góc của một tam giác khi biết tọa độ ba đỉnh.
• Tính nhanh thể tích tứ hiện, thể tích hình hộp khi biết tọa độ bốn đỉnh,…

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn