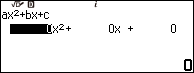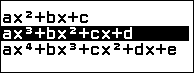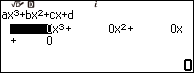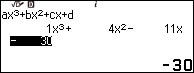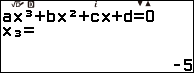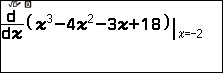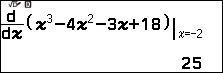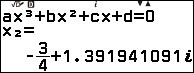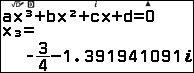Cách chia đa thức cho đa thức bậc ba bằng fx 880 BTG

Trong bài viết này mình sẽ hướng dẫn cho các bạn cách chia đa thức (bậc bất kì) cho đa thức bậc ba trên máy tính Casio fx 880 BTG.

Thủ thuật này sẽ giúp bạn tìm đa thức thương và đa thức dư một cách chính xác và nhanh chóng nhất.

#1. Nên áp dụng thủ thuật này khi nào?

Thủ thuật này chỉ áp dụng được với những đa thức chia có nghiệm thực, không phân biệt nghiệm đơn, nghiệm kép, nghiệm bội ba.

Nếu đa thức chia có nghiệm phức thì thủ thuật này không áp dụng được các bạn ha. Lúc này bạn cần thực hiện thủ thuật khác hoặc sử dụng kiến thức Toán học để giải.

Ngoài ra, bạn chỉ áp dụng được thủ thuật này trên Casio fx 880 BTG thôi ha, dòng máy Casio fx 580VN không thực hiện được vì không có tính năng bản tính Spreadsheet.

#2. Cần lưu ý gì khi sử dụng thủ thuật này?

Thứ nhất. Các hệ số của đa thức bị chia cần được nhập theo thứ tự lũy thừa giảm dần của biến và đầy đủ.

Chẳng hạn với đa thức bị chia $1 x^5 + 4 x^6 + 3 x^4 + 1 x^3 + 2 x^2 + 7$ chúng ta phải nhập là  4, 1, 3, 1, 2, 0, 7

Thứ hai. Việc xác định nghiệm của đa thức chia là nghiệm đơn, nghiệm kép, nghiệm bội ba rất quan trọng. Xác định sai, thương và dư sẽ sai theo.

Xem thêm:
Kiểm tra nghiệm của đa thức bậc ba là nghiệm đơn hay là nghiệm kép

Thứ ba. Nếu hệ số đứng trước $x^3$ của đa thức chia khác 1 thì chúng ta cần chia các giá trị của cột D cho hệ số đứng trước $x^3$, ngoại trừ ô cuối cùng.

Thứ tư. Bạn hãy cài đặt hiển thị nghiệm phức khi giải phương trình trước khi sử dụng thủ thuật này.

#3. Cài đặt hiển thị nghiệm phức

Mặc định nghiệm phức sẽ tự động hiển thị khi giải phương trình, trong trường hợp nghiệm phức không hiển thị thì bạn cần thực hiện tuần tự theo các bước.

Cách cài đặt trên fx 880 BTG:

Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK

 

Bước 2. Chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK

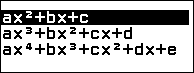
Bước 3. Nhấn phím TOOLS => chọn Complex Roots => nhấn phím OK => chọn On => nhấn phím OK

Bước 4. Nhấn phím AC

#4. Cách chia đa thức cho đa thức bằng máy Casio

Ví dụ 1. Tìm đa thức thương và đa thức dư của phép chia $4 x^6 + 1 x^5 + 3 x^4 + 1 x^3 + 2 x^2 + 2 x + 7$ cho $x^3 + 4 x^2 – 11 x – 30$

Bước 1. Sử dụng tính năng Equation (Polynomial) tìm nghiệm của đa thức chia $x^3 + 4 x^2 – 11 x – 30$

Bước 1.1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => chọn $ax^3+bx^2+cx+d$ => nhấn phím OK

Bước 1.2. Nhập 1 => nhấn phím EXE => nhập 4 => nhấn phím EXE => nhập -11 => nhấn phím EXE => -30 => nhấn phím EXE

Bước 1.3. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE

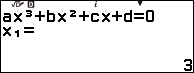
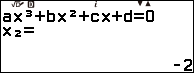
Suy ra đa thức chia $x^3 + 4 x^2 – 11 x – 30$ có ba nghiệm đơn là 3, -2 và -5

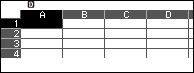
Bước 2. Mở ứng dụng bảng tính Spreadsheet

Nhấn phím HOME => chọn Spreadsheet => nhấn phím OK

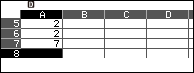
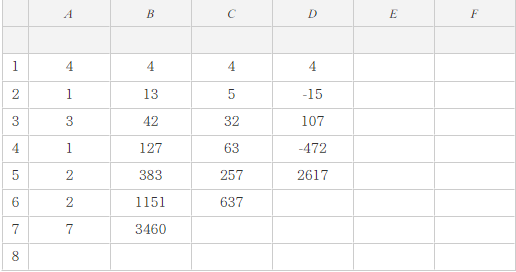
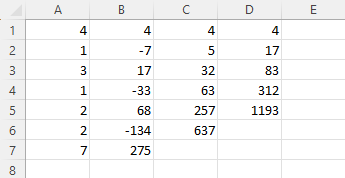
Bước 3. Lần lượt nhập các hệ số của đa thức bị chia 4, 1, 3, 1, 2, 2, 7 vào các ô A1, A2, A3, …, A7

Bước 4.

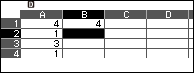
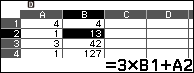
Bước 4.1. Nhập 4 (hệ số của $4x^6$) vào ô B1

Bước 4.2. Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK => nhập $3 \times B1+A2$ (3 là nghiệm thức nhất của đa thức chia) => nhấn phím EXE => nhập B2:B7 => nhấn phím EXE

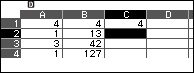
Bước 5.

Bước 5.1. Nhập 4 (hệ số của $4x^6$) vào ô C1

Bước 5.2. Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK => nhập $-2 \times C1+B2$ (-2 là nghiệm thức nhì của đa thức chia) => nhấn phím EXE => nhập C2:C6 => nhấn phím EXE

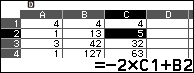
Bước 6.

Bước 6.1. Nhập 4 (hệ số của $4x^6$) vào ô D1

Bước 6.2. Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK => nhập $-5 \times D1+C2$ (-5 là nghiệm thức ba của đa thức chia) => nhấn phím EXE => nhập D2:D5 => nhấn phím EXE

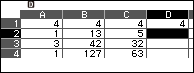
Vì hệ số đứng trước $x^3$ của đa thức chia $x^3 + 4 x^2 – 11 x – 30$ là 1 nên chúng ta không cần các chia các giá trị ở cột D cho 1

Vậy đa thức thương là $4x^3-15x^2+107x-472$ và đa thức dư là 2617(x-3)(x- -2)+637(x-3)+3460 hay $2617 x^2 – 1980 x – 14153$

Ví dụ 2. Tìm đa thức thương và đa thức dư của phép chia $4 x^6 + 1 x^5 + 3 x^4 + 1 x^3 + 2 x^2 + 2 x + 7$ cho $x^3 – 4 x^2 – 3 x + 18$

Thực hiện tương tự Bước 1 của Ví dụ 1 chúng ta tìm được nghiệm của đa thức chia $x^3 – 4 x^2 – 3 x + 18$ là -2 và 3

Đa thức bậc ba có hai nghiệm thì sẽ có một nghiệm đơn và một nghiệm kép. Bằng cách này hay cách khác chúng ta phải xác được đâu là nghiệm đơn, đâu là nghiệm kép.

Ở đây mình sẽ hướng dẫn các bạn xác định bằng cách dựa vào đạo hàm tại một điểm.

Đặt $f(x)=x^3 – 4 x^2 – 3 x + 18$

$f’(x)= 3 x^2 – 8 x – 3$

$f’(-2)=25 \neq 0$ nên -2 là nghiệm đơn và hiển nhiên 3 là nghiệm kép.

Thực hành trên fx 880 BTG

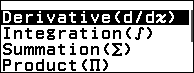
Bước 1. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative (d/dx) => nhấn phím OK

Bước 2. Nhập $x^3 – 4 x^2 – 3 x + 18$ => nhấp phím => nhập -2

Bước 3. Nhấn phím EXE

 

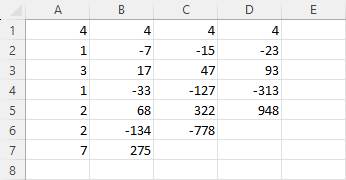
Thực hiện tương tự Bước 2 đến Bước 6 của Ví dụ 1 chúng ta thu được bảng tính Spreadsheet.

Vì hệ số đứng trước $x^3$ của đa thức chia là 1 nên chúng ta không các chia các giá trị ở cột D cho 1

Vậy đa thức thương là $4x^3+17x^2+83x+312$ và đa thức dư là $2617(x-3)(x- -2)+637(x-3)+3460$ hay $1193 x^2 – 556 x – 5609$

Ví dụ 3. Tìm đa thức thương và đa thức dư của phép chia $4 x^6 + 1 x^5 + 3 x^4 + 1 x^3 + 2 x^2 + 2 x + 7$ cho $2x^3 + 12 x^2 + 24 x + 16$

Thực hiện tương tự Bước 1 của Ví dụ 1 chúng ta tìm được nghiệm của đa thức chia $2x^3 + 12 x^2 + 24 x + 16$ là -2

Đa thức bậc ba có một nghiệm thực duy nhất thì nghiệm đó chắc chắn là nghiệm bội ba.

Thực hiện tương tự Bước 2 đến Bước 6 của Ví dụ 1 chúng ta thu được bảng tính Spreadsheet

Vì hệ số đứng trước $x^3$ của đa thức chia $2x^3 + 12 x^2 + 24 x + 16$ là 2 nên chúng ta phải các chia các giá trị ở cột D cho 2, ngoại trừ ô cuối cùng.

Vậy đa thức thương là $2x^3-\frac{23}{2}x^2+\frac{93}{2}x-\frac{313}{2}$ và đa thức dư là $948(x- -2)(x- -2)+ -778(x- -2)+275$ hay $948 x^2 + 3014 x + 2511$

Ví dụ 4. Tìm đa thức thương và đa thức dư của phép chia $4 x^6 + 1 x^5 + 3 x^4 + 1 x^3 + 2 x^2 + 2 x + 7$ cho $2 x^3 + 7 x^2 + 11 x + 10$

Thực hiện tương tự Bước 1 của Ví dụ 1 chúng ta tìm được nghiệm của đa thức chia $2x^3 + 12 x^2 + 24 x + 16$ là -2 và hai nghiệm phức liên hợp.

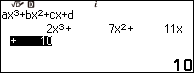
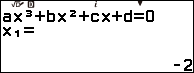
Vì đa thức chia có nghiệm phức nên thủ thuật không khả dụng.

#5. Lời kết

Trên đây là chi tiết các bước chia đa thức cho đa thức bậc ba. Thủ thuật này sẽ giúp bạn xác định đa thức thương và đa thức dư một cách chính xác và nhanh chóng.

Rất tiếc là thủ thuật không khả dụng khi đa thức bậc ba có nghiệm phức, hy vọng trong thời gian sắp tới, hạn chế này sẽ được hãng Casio giải quyết.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách tìm cực trị của hàm số đa thức (bậc 2 và bậc 3)
• 2 cách chia đa thức bằng Hoocne, Hoocne bằng máy tính
• Cách phân tích đa thức thành nhân tử bằng máy tính CASIO

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn