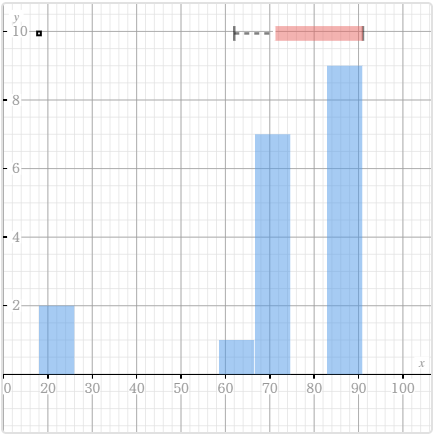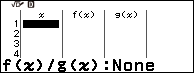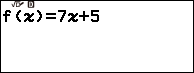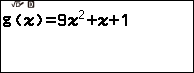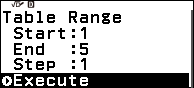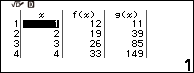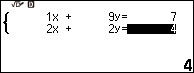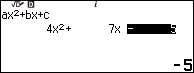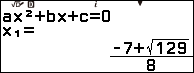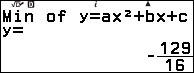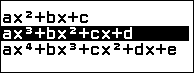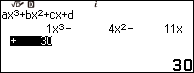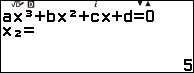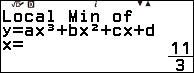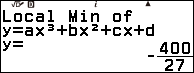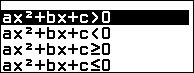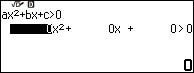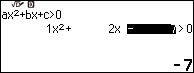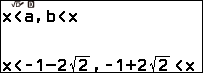Chào các bạn, tính năng QR Code là một trong những tính năng mới nổi bật nhất của dòng máy tính Casio fx 880 BTG.
Tính năng này cho phép chúng ta xuất ra mã QR từ màn hình kết quả, rồi sử dụng smartphone để quét mã này sẽ dẫn chúng ta đến trang https://classpad.net
Lúc này Classpad sẽ hiển thị đồ thị của hàm số, hoặc biểu đồ của bảng thống kê, hoặc… Nói chung là hiển thị cái gì thì phụ thuộc vào màn hình kết quả mà bạn sử dụng để tạo mã QR.
Mục Lục Nội Dung
#1. Cách quét mã QR trên các phiên bản Casio fx 880
Tùy thuộc vào phiên bản fx 880 BTG bạn đang sử dụng mà cách quét mã QR sẽ có một số khác biệt.
- Nếu bạn sử dụng phiên bản Vật lý thì sử dụng điện thoại thông minh để quét.
- Nếu bạn sử dụng phiên bản giả lập chạy trên máy vi tính thì khi xuất ra bạn chỉ cần nháy chuột phải vào nó.
- Nếu bạn sử dụng phiên bản giả lập chạy trên nền Web thì chỉ cần nháy chuột vào công cụ Sticky output.
#2. Màn hình kết quả có giá trị khi xuất ra mã QR
Về cơ bản thì màn hình kết quả nào cũng cho phép chúng ta xuất ra mã QR, nhưng không phải lúc nào cũng mang lại giá trị.
Dưới đây là một số màn hình kết quả mà khi xuất ra mã QR sẽ mang lại lợi ích trong học tập và giảng dạy.
- Bảng thống kê Statistics.
- Bảng giá trị Table.
- Hệ hai phương trình.
- Phương trình (bậc hai, bậc ba)
- Bất phương trình (bậc hai, bậc ba, bậc bốn)
- Phân phối…
#3. Cách sử dụng tính năng QR Code trên Caiso 880 BTG
3.1. Vẽ biểu đồ
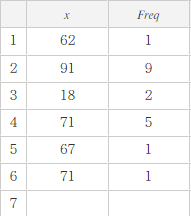
Vẽ biểu đồ minh họa cho bảng số liệu thống kê bên dưới.
| Giá trị | 62 | 91 | 18 | 71 | 67 | 71 |
| Tần số | 1 | 9 | 2 | 5 | 1 | 1 |
Bước 1. Nhấn phím HOME => chọn Statistics => nhấn phím OK => chọn 1-Variable => nhấn phím OK


Bước 2. Nhấn phím TOOLS => chọn Frequency => nhấn phím OK => chọn On => nhấn phím OK => nhấn phím AC


Bước 3.
Bước 3.1. Nhập giá trị thứ nhất => nhấn phím EXE => nhập giá trị thứ nhì => nhấn phím EXE => nhập giá trị thứ ba => nhấn phím EXE => …
Bước 3.2. Nhấn phím => nhấn phím
Bước 3.3. Nhập tần số thứ nhất => nhấn phím EXE => nhập tần số thứ nhì=> nhấn phím EXE => nhập tần số thứ ba => nhấn phím EXE => …
Bước 4. Nhấn phím SHIFT => nhấn phím x
Bước 5. Sử dụng điện thoại thông minh quét mã QR
3.2. Vẽ đồ thị của hàm số
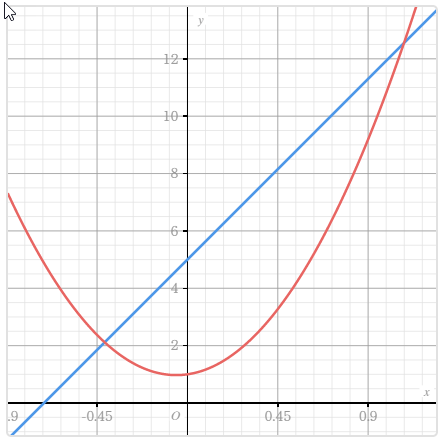
Vẽ đồ thị của hàm số y=7x+5 và hàm số $y=9x^2+x+1$ trên cùng một hệ trục tọa độ
Bước 1. Nhấn phím HOME => chọn Table => nhấn phím OK

Bước 2. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK => nhập hàm số 7x+5 => nhấn phím OK
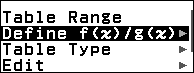
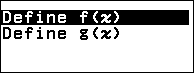
Bước 3. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define g(x) => nhấn phím OK => nhập hàm số $9x^2+x+1$ => nhấn phím OK
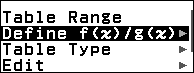
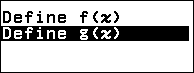
Bước 4. Nhấn phím TOOLS => chọn Table Range => nhấn phím OK
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
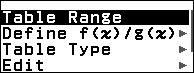
Bước 5. Nhấn phím EXE
Bước 6. Nhấn phím SHIFT => nhấn phím x
Bước 7. Sử dụng điện thoại thông minh quét mã QR
3.3. Biểu diễn tập nghiệm của hệ hai phương trình
Biểu diễn nghiệm của hệ phương trình hai phương trình $\left\{\begin{array}{}x+9y=7\\2x+2y=4\end{array}\right.$
Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Simul Equation => nhấn phím OK => chọn 2 Unknowns => nhấn phím OK


Bước 2. Nhập 1 => nhấn phím EXE => nhập 9 => nhấn phím EXE => nhập 7 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập 4 => nhấn phím EXE
Bước 3. Nhấn phím EXE => nhấn phím EXE

Bước 4. Nhấn phím SHIFT => nhấn phím x
Bước 5. Sử dụng điện thoại thông minh quét mã QR
3.4. Vẽ đồ thị của hàm số bậc hai
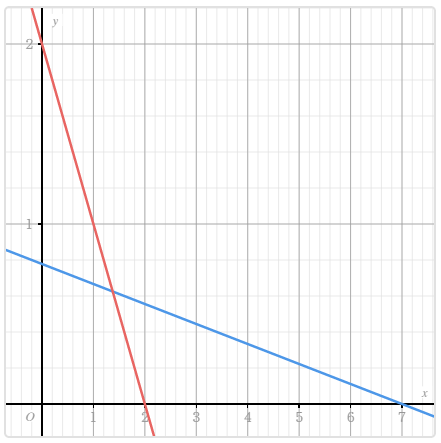
Vẽ đồ thị, cực trị và giao điểm với trục hoành của hàm số bậc hai $y=4x^2+7x-5$
Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK


Bước 2. Nhập 4 => nhấn phím EXE => nhập 7 => nhấn phím EXE => nhập -5 => nhấn phím EXE
Bước 3. Nhấn phím EXE => nhấn phím EXE
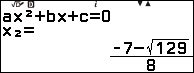
Bước 4. Nhấn phím EXE => nhấn phím EXE
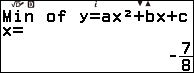
Bước 5. Nhấn phím SHIFT => nhấn phím x
Bước 6. Sử dụng điện thoại thông minh quét mã QR
Chú ý.
Ngoài cách trên bạn cũng có thể vẽ đồ thị của hàm số $y=4x^2+7x-5$ bằng cách tạo bảng giá trị Table, tuy nhiên bạn sẽ không thu được tọa độ của điểm cực trị và giao điểm với trục hoành (nếu có)
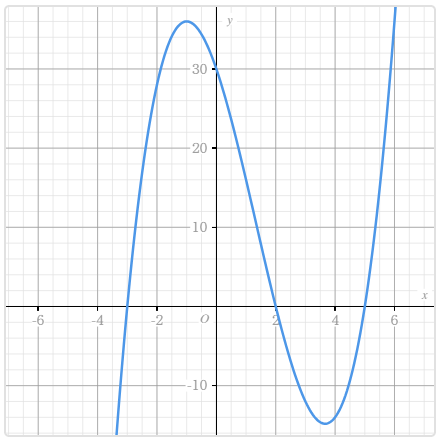
3.5. Vẽ đồ thị của hàm số bậc ba
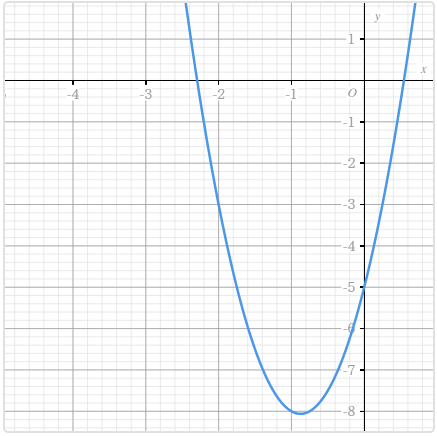
Vẽ đồ thị, cực trị và giao điểm với trục hoành của hàm số bậc ba $y=x^3-4x^2-11x+30$
Bước 1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^3+bx^2+cx+d$ => nhấn phím OK


Bước 2. Nhập 1 => nhấn phím EXE => nhập -4 => nhấn phím EXE => nhập -11 => nhấn phím EXE => nhập 30 => nhấn phím EXE
Bước 3. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE
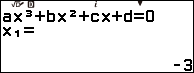
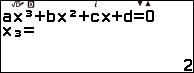
Bước 4. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE => nhấn phím EXE
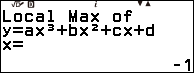
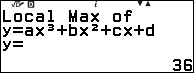
Bước 5. Nhấn phím SHIFT => nhấn phím x
Bước 6. Sử dụng điện thoại thông minh quét mã QR
Chú ý.
Ngoài cách trên bạn cũng có thể vẽ đồ thị của hàm số $y=x^3-4x^2-11x+30$ bằng cách tạo bảng giá trị Table.
Tuy nhiên bạn sẽ không thu được tọa độ của điểm cực trị và giao điểm với trục hoành (nếu có).
3.6. Biểu diễn tập nghiệm của bất phương trình
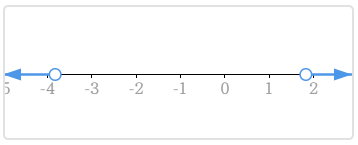
Biểu diễn tập nghiệm của bất phương trình bậc hai $x^2+2x-7>0$
Bước 1. Nhấn phím HOME => chọn Inequality => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK => chọn $ax^2+bx+c>0$ => nhấn phím OK

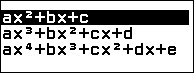
Bước 2. Nhập 1 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập -7 => nhấn phím EXE
Bước 3. Nhấn phím EXE
Bước 4. Nhấn phím SHIFT => nhấn phím x
Bước 5. Sử dụng điện thoại thông minh quét mã QR
- Phần được tô đậm màu xanh lam chính là tập nghiệm của bất phương trình đã cho.
- Nếu tập nghiệm của bất phương trình là nửa khoảng hoặc đoạn thì đường tròn sẽ được tô kính.
#7. Lời kết
Vâng, trên đây là chi tiết các bước sử dụng tính năng QR Code của fx 880 BTG.
Việc sử dụng tính năng này rất đơn giản, mấu chốt là biết được màn hình kết quả nào có giá trị trong học tập và giảng dạy.
Ngoài các màn hình trên, màn hình phân phối (phân phối nhị thức, phân phối mật độ xác suất chuẩn, …) cũng có giá trị.
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.
Kiên Nguyễn – Blog Chia Sẻ Kiến Thức !
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống