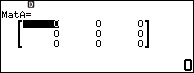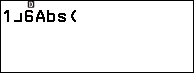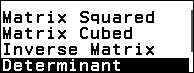Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Trong bài viết này mình sẽ hướng dẫn các bạn sử dụng máy tính CASIO để tính nhanh thể tích của khối tứ diện khi biết tọa độ bốn đỉnh.
Việc tính thể tích của khối tứ diện khi biết tọa độ bốn đỉnh có khá nhiều cách, tuy nhiên, nếu tính bằng máy tính CASIO thì chỉ có hai cách mà thôi. Cụ thể là:
- Cách 1. Dựa vào tích hỗn tạp (tích hỗn hợp)
- Cách 2. Dựa vào ma trận vuông cấp 3 x 3
Tuy nhiên, trong phạm vi ngắn gọn của bài viết này mình chỉ hướng dẫn cho các bạn Cách 2 thôi ha.
Mặc dù Cách 2 không phù hợp với học sinh THPT nhưng với các bài kiểm tra, các bài thi trắc nghiệm, quan trọng là chính xác và nhanh chóng.
Mục Lục Nội Dung
#1. Công thức tính thể tích tứ diện
Trong không gian Oxyz cho điểm $A=(x_a, y_a, z_a); B=(x_b, y_b, z_b); C=(x_c, y_c, z_c)$ và $D=(x_d, y_d, z_d)$
Bước 1. Tính véc tơ $\overrightarrow{AB}, \overrightarrow{AC}$ và $\overrightarrow{AD}$
Giả sử véc tơ $\overrightarrow{AB}=(o, p, q); \overrightarrow{AC}=(r, s, t)$ và $\overrightarrow{AD}=(u, v, w)$
Bước 2. Gán ma trận vuông cấp 3 x 3 $\left[\begin{array}{}o&p&q\\r&s&t\\u&v&w\end{array}\right]$ vào biến nhớ ma trận MatA
Bước 3. Sử dụng công thức $V_{ABCD}=\frac{1}{6}\left|\left|MatA\right|\right|$
#2. Cách tính thể tích tứ diện trên Casio fx 880 BTG
Ví dụ 1. Tính thể tích khối tứ diện ABCD biết điểm A=(0,0,2); B=(-3,0,0); C=(5,0,0) và D=(0,7,0)
Bước 1. Tính véc tơ $\overrightarrow{AB}, \overrightarrow{AC}$ và $\overrightarrow{AD}$
Chúng ta dễ dàng tính được véc tơ $\overrightarrow{AB}=(-3, 0, -2); \overrightarrow{AC}=(5, 0, -2)$ và $\overrightarrow{AD}=(0, 7, -2)$
Bước 2. Gán ma trận vuông cấp 3 x 3 $\left[\begin{array}{}-3&0&-2\\5&0&-2\\0&7&-2\end{array}\right]$ vào biến nhớ ma trận MatA
Bước 2.1. Nhấn phím HOME => chọn Matrix => nhấn phím OK
Bước 2.2. Nhấn phím TOOLS => chọn MatA => nhấn phím OK => chọn Rows
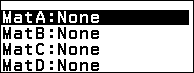
Tiếp tục nhấn phím OK => chọn 3 Rows => nhấn phím OK => chọn Columns => nhấn phím OK => chọn 3 Columns => nhấn phím OK => nhấn phím OK
Bước 2.3. Lần lượt nhấn các phím 
Bước 2.4. Nhấn phím EXE
Bước 3. Sử dụng công thức $V_{ABCD}=\frac{1}{6}\left|\left|MatA\right|\right|$
Bước 3.1. Nhập $\frac{1}{6}$
Bước 3.2. Nhấn phím CATALOG => chọn Numeric Calc => nhấn phím OK => chọn Absolute Value => nhấn phím OK
Bước 3.3. Nhấn phím CATALOG => chọn Matrix => nhấn phím OK => chọn Matrix Calc => nhấn phím OK => chọn Determinant => nhấn phím OK
Bước 3.4. Nhấn phím CATALOG => chọn Matrix => nhấn phím OK => chọn MatA => nhấn phím OK
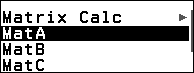
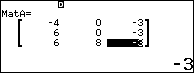
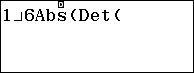
Bước 3.5 Nhấn phím EXE
Vậy thể tích của khối tứ diện ABCD đã cho bằng $\frac{56}{3}$ (đơn vị thể tích)
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
#3. Bấm máy tính thể tích tứ diện trên Casio 580 VNX
Ví dụ 2. Tính thể tích của khối tứ diện ABCD biết điểm A=(0,0,3); B=(-4,0,0); C=(6,0,0) và D=(0,8,0)
Bước 1. Tính véc tơ $\overrightarrow{AB}, \overrightarrow{AC}$ và $\overrightarrow{AD}$
Chúng ta dễ dàng tính được véc tơ $\overrightarrow{AB}=(-4, 0, -3); \overrightarrow{AC}=(6, 0, -3)$ và $\overrightarrow{AD}=(0, 8, -3)$
Bước 2. Gán ma trận vuông cấp 3 x 3 $\left[\begin{array}{}-4&0&-3\\6&0&-3\\0&8&-3\end{array}\right]$ vào biến nhớ ma trận MatA
Bước 2.1. Nhấn phím MENU => chọn Matrix => nhấn phím = => nhấn phím AC
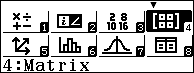
Bước 2.2. Nhấn phím OPTN => nhấn phím 1 => nhấn phím 1 => nhấn phím 3 => nhấn phím 3
Bước 2.3. Lần lượt nhấn các phím sau:
Bước 2.4 Nhấn phím AC
Bước 3. Sử dụng công thức $V_{ABCD}=\frac{1}{6}\left|\left|MatA\right|\right|$
Bước 3.1. Nhập $\frac{1}{6}$
Bước 3.2. Nhấn phím SHIFT => nhấn phím (
Bước 3.3. Nhấn phím OPTN => nhấn phím 
=> nhấn phím 2 để chọn Determinant
Bước 3.4. Nhấn phím OPTN => nhấn phím 3 để chọn MatA
Bước 3.5 Nhấn phím =
Vậy thể tích của khối tứ diện ABCD đã cho bằng 40 (đơn vị thể tích)
#4. Lời kết
Vâng, trên đây là cách sử dụng máy tính Casio để tính nhanh diện diện tứ diện mà mình muốn chia sẻ đến các bạn.
Để tiết kiệm thời gian khi tính thể tích của khối tứ diện khi biết tọa độ bốn đỉnh bằng máy tính CASIO thì bạn có thể bỏ qua việc nhập giá trị tuyệt đối.
Nếu kết quả là số âm thì bạn chỉ việc lấy số dương tương ứng.
Trường hợp đề yêu cầu tính thể tích của khối hộp thì bạn hãy gấp 6 lần thể tích của khối tứ diện.
Chẳng hạn thể tích của khối hộp tạo bởi điểm A=(0,0,2); B=(-3,0,0); C=(5,0,0) và D=(0,7,0) là 112 (đơn vị thể tích)
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.
Đọc thêm:
- Cách tính thể tích tứ diện trong không gian (công thức & casio)
- Tính diện tích, thể tích của hình lăng trụ đứng tam giác, tứ giác
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
